从子列的视角来判定等差（比）数列

江苏省常州高级中学 陈小红

结论1．设k为给定的不小于2的正整数，若数列｛an｝的前k项构成公差为d的等差数列，且子列｛akn-s｝（其中s=0，1，2，…，k-1）都是公差为kd的等差数列，则｛an｝是等差数列．

结论2．设k为给定的不小于2的正整数，若数列｛an｝的前k项构成公比为q的等比数列，且子列｛akn-s｝（其中s=0，1，2，…，k-1）都是公比为qk的等比数列，则｛an｝是等比数列．

结论1的证明：因为｛akn-s｝（其中s=0，1，2，…，k-1）是公差为kd的等差数列，

所以akn-s=ak-s+（n-1）kd；又因为a1，a2，…，ak构成公差为d的等差数列，

所以ak-s=a1+（k-s-1）d，于是akn-s=a1+（k-s-1）d+（n-1）kd=a1+（kns-1）d．

注意到每一个正整数都可以表示成kn-s（其中s=0，1，2，…，k-1）的形式，故对于任意的n∈N*，都有an=a1+（n-1）d．因此对任意的n∈N*，都有an+1-an=d，于是｛an｝是等差数列．

结论2的证明完全类似，此处不再赘述．

两个结论本身并不重要，但其证明的过程却给出了证明等差（比）数列的一个新的视角，即从子列的视角，先求出子列的通项公式进而得出原数列的通项公式，再利用通项公式证明数列为等差（比）数列．下面，举两例来说明如何使用这样的方法解题．

例1设数列｛an｝的各项均为正数，若对于任意的n∈N*，存在k∈N*，使得a2n+k=anan+2k成立，则称数列｛an｝为“Jk型”数列．若数列｛an｝既是“J3型”数列，又是“J4型”数列．

求证：数列｛an｝为等比数列．

分析 根据“J4型”数列的定义，数列a1，a5，a9，a13，a17，a21，…为等比数列，设其公比为Q．根据“J3型”数列的定义，数列a1，a4，a7，…，a3n-2，…为等比数列，设其公比为q1，数列a2，a5，a8，…，a3n-1，…为等比数列，设其公比为q2，数列a3，a6，a9，…，a3n，…为等比数列，设其公比为q3．通过列出各数列的尽可能多的项并观察可以发现，前面三个等比数列中都有某些项总在公比为Q的等比数列a1，a5，a9，a13，a17，a21，…中出现，这样就可以得出q1，q2，q3与Q的关系，从而可用Q表示q1，q2，q3，进而用a1与Q表示数列｛a3n-2｝，｛a3n-1｝，｛a3n｝的通项公式，再得出原数列的通项公式，最后可利用通项公式来证明等比数列．

证明 因为数列｛an｝是“J3型”数列，所以对任意的n∈N*恒成立，又数列｛an｝的各项均为正数，所以an，an+3，an+6成等比数列，则数列｛a3n-2｝，｛a3n-1｝，｛a3n｝都是等比数列，设它们的公比分别为q1，q2，q3．因为数列｛an｝是“J4型”数列，所以anan+8对任意的n∈N*恒成立，又数列｛an｝的各项均为正数，所以an，an+4，an+8成等比数列．因此，a1，a5，a9，a13，a17，a21，…为等比数列，设其公比为Q．

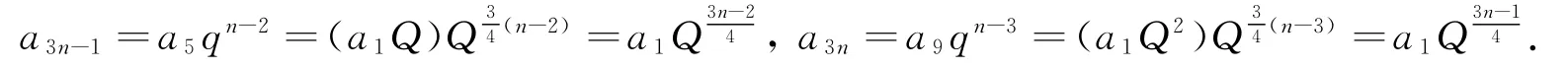
点评 解答中有两个关键步骤．其一，利用a1与a13，a5与a17，a9与a21在不同的等比数列中的关系来证明3个公比相等；其二，表达出三个子列的通项公式，此处a3n-1用a5来表示，a3n用a9来表示，原因是a5，a9都可很方便地用a1与Q表示．

例2对于给定的正整数k，若数列｛an｝满足an-k+an-k+1+…+an-1+an+1+…+an+k-1+an+k=2kan对任意正整数n（n＞k）总成立，则称数列｛an｝是“P（k）数列”．

（1）略；

（2）若数列｛an｝既是“P（2）数列”，又是“P（3）数列”，证明：｛an｝是等差数列．

分析 根据“P（2）数列”与“P（3）数列”的定义，很容易得到an-2+an-1+an+1+an+2=4an（n≥3），an-3+an-2+an-1+an+1+an+2+an+3=6an（n≥4），两式作差得出an-3+an+3=2an对n≥4恒成立，则三个子数列｛a3n-2｝，｛a3n-1｝，｛a3n｝都是等差数列．若设这三个等差数列的公差分别为d1，d2，d3，再设法证明三个公差相等．若在等式an-2+an-1+an+1+an+2=4an（n≥3）中分别赋值n=3和n=6，这样两式相减就只有d1，d2，d3的等式，类似地再赋一些合适的值得出d1，d2，d3的其他等式，通过方程组思想证明d1=d2=d3．然后再通过赋值研究a1，a2，a3之间的关系，即可用a1与d1表示数列｛a3n-2｝，｛a3n-1｝，｛a3n｝的通项公式．再得出原数列的通项公式，最后可利用通项公式来证明等差数列．

证明 （2）因为数列｛an｝是“P（2）数列”，所以an-2+an-1+an+1+an+2=4an①对n≥3，且n∈N*恒成立．又因为数列｛an｝是“P（3）数列”，所以an-3+an-2+an-1+an+1+an+2+an+3=6an②对n≥4，且n∈N*恒成立．

②—①得，an-3+an+3=2an对n≥4，且n∈N*恒成立，即an-3，an，an+3成等差数列，则数列｛a3n-2｝，｛a3n-1｝，｛a3n｝都是等差数列，设公差分别为d1，d2，d3．

由①得a1+a2+a4+a5=4a3③，a4+a5+a7+a8=4a6④，则由④-③得，2d1+2d2=4d3，即d1+d2=2d3；

由①得a2+a3+a5+a6=4a4⑤，a5+a6+a8+a9=4a7⑥，则由⑥-⑤得，2d2+2d3=4d1，即d2+d3=2d1；

由①得a3+a4+a6+a7=4a5⑦，a6+a7+a9+a10=4a8⑧，则由⑧-⑦得，2d3+2d1=4d2，即d3+d1=2d2．

因此，d1=d2=d3，故可令d1=d2=d3=d．

由③得到a1+a2+d=2a3，由⑤得到a2+a3=2a1+d，

点评 类似于例1，本题解答中也有两个关键步骤．其一，利用赋值得到相关的方程组来证明3个公差相等，赋值时可使两等式中对应项的下标相差3，两等式作差后的等式中仅有字母d1，d2，d3；其二，是寻找a1，a2，a3的关系，也是通过赋值得到方程组并解方程组得到，在方程组中视a1与d为已知，视a2与a3为未知．

前面所举的两例难度比较大，给出的解法的共性是明显的，即从它们的子列的通项入手进行深入分析，合理地研究某些项在不同的数列中的关系或者恰当地赋值得出方程组进而得出子列的公差（比）相等，得出子列的通项公式，最后给出原数列的通项公式，再判断数列为等差（比）数列．当然，对于例2还有其他的解法，本文仅仅是提供了一种解决这类问题的视角以分享．