一道等差数阵题的畅想曲

马思琪

高一下学期，我们学习了《必修5》中的数列知识，在做练习作业时，发现了这道题：

下面给出一个“等差数阵”：

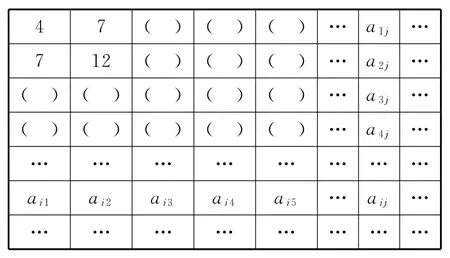
图1

其中每行、每列都是等差数列，aij表示位于第i行第j列的数．

（1）写出a45的值；

（2）写出aij的计算公式，以及2 017这个数在等差数阵中所在的一个位置．

认真做完题目，我掩卷沉思，不禁思绪翩翩．这样根据已知数据，寻找恰当规律，填数的数阵，在小学也见过．现在我是高中生，长大了，问题也升级了，这个有意思．我就以这道题为契机，自主设置问题进行探索求解——进行一番数学畅想．

为了完成第（1）小题和找规律，我一定要不辞辛劳地多写一些项，如图2．这样就轻松得到第（1）小题答案49．

第（2）小题要求解aij的通项公式．平时学的数列通项，只有一个变量，这个题目搞事情呀，怎么是双变量呢？看着图2中大量的数据和省略号，我心中不觉阵阵发毛，想必难写！怎么办？

不过要找出2 017在等差数阵中的一个位置，可以在较小的行列中进行试探．观察数阵发现，这个数阵的数关于aii成对称排列，即第一行的数和第一列的数一样，第i行和第i列的数一样，那么某数在aij位置出现，就必在aji位置出现．如果2 017出现在第一行，必有2 017=4+3（j-1），解得j=672，故2 017出现在第1行第672列中，当然也出现在第672行第1列中．它还会出现在别的位置吗？继续用这个办法试探所有的，哦，NO，饶了我吧，这一定不是明智的想法，它定会有规律可循的，我得慢慢研究它．

图2

畅想一：方阵畅想曲

我仔细观察这些数据，嘿嘿，有了．从图2中选取n行n列的方阵，对角线上行和列是相同的，相当于一个变量，应该简单得多，我先来解决它．

问题1 在这个数据表中，画出数据方阵，观察对角线有什么变化规律？

分析 从图2中发现，对角线所在数据依次为：4，12，24，40，60，84…找出关系式：an，n-an-1，n-1=4n．

问题2 根据上式关系，可以求出｛an，n｝的通项吗？

分析 这个问题，就是老师讲得烂熟的累加法，也是等差数列通项公式的一种求解方法．于是：

an，n=（an，n-an-1，n-1）+（an-1，n-1-an-2，n-2）+…+（a2，2-a1，1）+a1，1=4n+4（n-1）+4（n-2）+…+4×2+4=4（1+

分析 先来变形该数列的通项表达式，再决定使用什么方法求解．于是有这个通项被裂开成两项，且恰好前一项和后一项相加，能够抵消掉两项，依此类推，就可以求得前n项和的前n项求和，运用了裂项法，其实质和问题2的累加法一样的．记得老师还形象地形容说：这是一种自杀式的求法，它们相互干仗，直到消灭得只剩一头一尾，不过，要弄清除头和尾外到底还剩余多少项．

完成了对角线的通项，我们把目光再次转移到任意方阵中来：任意一项的通项如何表示？如何判定任给一个数是否在这个方阵中？如果在，会出现多少次呢？

畅想二：矩阵畅想曲

用i，j直接表示aij的通项有困难，考虑到题目说每行、每列都是等差数列，我是不是可以采用迂回的方法，先表示每行或者每列的通项，再进行观察呢？说干就干．

问题4 用j来 表 示a1，j，a2，j，a3，j，a4，j，a5，j的通项，从而能得出aij的表达式吗？

分析 其实就是要将各行的通项表达出来，再归纳得出aij的通项．观察图2，得到各行的公差是3，5，7，9，11，…等依次增加的奇数．于是有：a1，j=3j+1；a2，j=5j+2；a3，j=7j+3；a4，j=9j+4；a5，j=11j+5，…由这一些式子，可 以归纳出ai，j=（2i+1）j+i=2ij+i+j．

由此表达式可以得到：

1．ai，j=aj，i；

2．当i=j时，ai，i=2i（i+1），此数为4的倍数．

问题5 还能有别的方法求出aij的表达式吗？

分析 因为这个数阵是每行每列都为等差数列的数阵，所以只要算出aij所在行或者列的第一个数，再运用等差数列通项公式就可以算出aij的通项．我选择先计算ai，1，即第一列的第i个数，ai，1=4+3（i-1）=3i+1，又因为第一行、第二行、第三行……的公差依次是3，5，7，…，可以得到第i行的公差为2i+1，于是有：ai，j=3i+1+（2i+1）（j-1）=2ij+i+j．

问题6 根据所得表达式，找出原题中的2 017这个数在这个数阵中的位置；2 018这个数在数阵中吗？出现多少次？

分析 要求解2 017在这个数阵中的位置，就是解出i和j．ai，j=2ij+i+j=2 017，整理得到：因为i和j都是正整数，故4 035必是2i+1的倍数．又因为4 035=3×5×269，所以4 035的因数有1，3，5，15，269，807，1 345，4 035共8个．因此解的情况列表为：

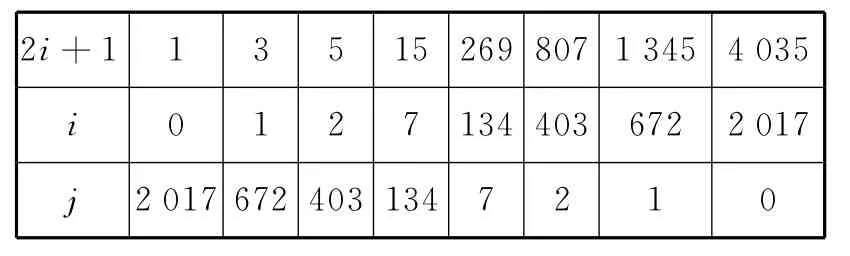
表1

舍去使i或j为0的解，共得到6组满足条件的i和j，因此2 017在数阵中出现了6次．按（i，j）的这个数对形式依次是（1，672），（672，1），（2，403），（403，2），（7，134），（134，7）．

同理可解得2 018在这个数阵中出现2次，对应位置是（5，183），（183，5）．

分析 由ai，j=2ij+i+j，可以得到an，1=3n+1，an+1，1=3n+4，因此裂项后，就可以轻松解得前n项和为

根据此问题，进行联想，还可以设置一些类似的题目，进行练习，如：

畅想三：多媒体畅想曲

问题8 借用Excel表格，如何寻找规律呢？

分析 Excel有强大的运算与分析能力，丰富的功能区菜单，面对大数据工作表的时候，进行数据整理、计算、汇总、查询、分析等处理，简直无所不能，太赞了！

我运用Excel表格，查找2 017这个数在等差数阵中所在的一个位置，使用了如下方法．

借用Excel的妙算畅想曲．

步骤1：由通项ai，j=2ij+i+j=2 017，得到

步骤2：打开Excel表格，在A1、B1、A2、A3中输入i，j，1，2，选中A2和A3，向下拉复制句柄，直到达到数字不超过2 017的最大行Int（（2 017-4）／3+1）=672为止．

步骤3：在B2中输入“=（2 017-A2）／（2*A2+1）”，双击单元格B2右下角的复制句柄，得到i所对应的j值，j值为正整数的即为满足条件的解．

步骤4：对第二列数进行取余数，并把结果放在第3列中，在第3列中进行升序或者筛选出余数为0，就得到所求的i和j了，如图3．当然也可以采用别的办法选出满足条件的i和j．

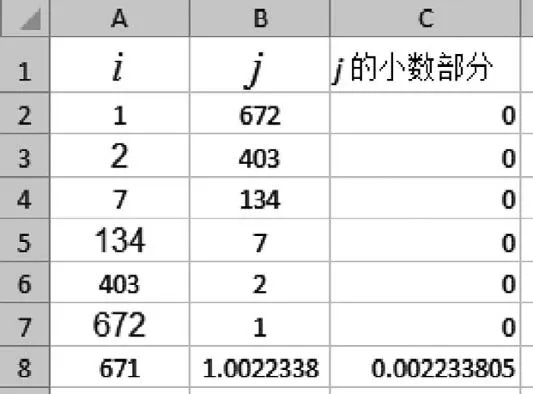
图3

问题9 运用编程的方式解决问题，会否更方便呢？

我们现在正在学习Visual Basic语言编程，这道题目也符合编程的要求，不妨小试一下牛刀，从两个不同角度编写一下查找某数在等差数阵中的位置的程序，编写的程序及结果如图4和图5所示．

运行该程序，只要在方框内输入你想查找的数字，单击查找，在窗体上就会列出该数字对应的i，j的值，从而得出该数在数阵表格中的位置．

图4是运用了已经算出的aij=2ij+i+j这个通式，运用二维数组进行编程设计的．图5是运用了表格中给出的4个数字4，7，7，12，根据等差中项的性质，先算出第一行和第二行的各数，即i=1，2时，用公式a（i，j）=2*a（i，j-1）-a（i，j-2）计算出第一、二行．对于给定的数M，第一行可能出现的最大的列数是Int（（m-4）／3+1），下一列的数就超出M了．这个数就是最大的列数和行数．然后再利用a（i，j）=2*a（i-1，j）-a（i-2，j）计算其余的各行，直到最大的行．

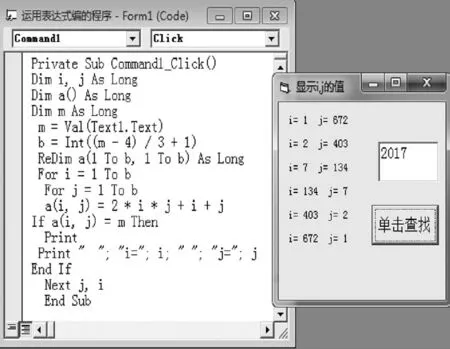
图4

图5

畅想四：数阵变奏曲

对上面的表格进行改编，一定可以得到一些有趣的规律．

改编一：使每行的公差始终为3，每列公差为5．除了前面的问题，还可以提出如下问题．

1．哪些数会在这个数阵中出现，哪些数不会出现？有规律可循吗？

2．哪些数会出现两次？三次？甚至无数多次？有规律或者公式吗？

………

改编二：n2（n≥4）个正数排成n行n列的方阵：

a 11 a 12 a 13 a 14…a 1n a 21 a 22 a 23 a 24…a 2n a 31 a 32 a 33 a 34…a 3n a 41 a 42 a 43 a 44…a 4n………………a n 1 a n 2 a n 3 a n 4…a nn

其中第一行的数成等差数列，每一列中的数成等比数列，并且所有公比都相等，已知

2．计算对角线所在数列ann｛ ｝的前n项和．

3．写出aij的计算公式，以及这个数在此数阵中所在的一个位置．（注：aij表示位于第i行第j列的数）

……

数字构成的数阵，千变万化，只要你开洞大脑，不断思考，你就可以收获一片旖旎，欣赏无限绚丽的风光，奏响一段惬意的畅想曲．

【指导老师点评】

马思琪同学在作业中发现了一道有趣的等差数阵问题，循着问题的脚步，不断探究，运用代数、Excel、编程三种办法找出2017在等差数阵的位置，而且通过ai，j的通项设置出裂项求和等数列问题．善于学习思考和运用多媒体工具解决问题是本文的一大特色，尽管学校学了一些VB编程语言，但要完成没有学过的二维数组随变量而精确定义，以及For语句与IF语句的嵌套运用，还是困难不小，学习就是在这种自发的“尝试与错误”过程中完成的．