关注中等生考试状态下的“会而不对”现象——基于错位相减法的解题调查与分析

(大厂高级中学,江苏 南京 210044)

1 背景

文献[1]指出“会而不对”现象是指拿到题目后，感觉会做，也能下笔求解，却做不出正确答案的现象.其实这是一个永恒的话题.“如何有效地减少这种现象的发生”成为教师与学生共同关注的问题.根据笔者的教学实践和调查发现：中等生出现这种现象尤为明显，特别是在考试状态下.笔者收集中等生考试状态下“会而不对”现象的典型案例，探究其原因，并给出减少这种现象的策略.

基于2018年6月底江苏省南京市高一数学统测及网上阅卷情况，笔者对南京市的3所高中(两所四星高中、一所三星高中)的1 208名学生的解答情况进行得分统计，通过错解收集分析以及个别学生和教师的访谈，发现中等生考试状态下产生“会而不对”现象的原因，寻求减少这种现象的有效方法和教学策略.

2 题目与得分情况

题目已知{an}是公差不为0的等差数列,{bn}是等比数列,且a2=b2=1,a3-1=b3,a4-1=b4.

1)求数列{an},{bn}的通项公式；

2)记cn=anbn，求数列{cn}的前n项和Sn；

(江苏省南京市2017学年第二学期高一数学期末统考第20题)

说明整卷满分160分，平均分108.76，难度系数为0.68.

表1 第20题的得分情况

由表1可以看出，第2)小题难度系数为0.44，属于中档题，区分度为0.93，具有较高的区分度.第20题的3个小题中，第2)小题更能反映出中等生的解题状况，下面仅对第2)小题进行数据统计和分析.

表2 第2)小题的得分情况

续表2

由表2可以看出，第1)小题正确、第2)小题有解答但未得分及得分不全的学生数为615人，占参加考试学生总数的50.91%，不妨称这部分学生为中等生.

3 第2)小题的典型错误及错因分析

由第1)小题知an=2n-3,bn=2n-2，本文的案例仅针对第1)小题正确但第2)小题错误的学生.

3.1 写Sn的展开式出错

图1中的第4行出错，生1把第3行的“2n-3”看成了“2(n-3)”，导致后续全部出错.展现出生1的运算素养较弱，数学运算总是在明晰运算对象的基础上进行的，但该生把运算对象看错了，实际上是短时记忆的准确性不够.

图1

3.2 乘公比出错

图2中的第3行出错，生2在等式两边乘以公比2时，最后一项“(2n-5)2n-2”与“ (2n-3) 2n-1”顺序颠倒, 导致该生在相减时最后一项出错.

图2

3.3 相减出错

图3中两边乘以公比2是正确的，但在第3行相减时出错，等式右边括号内的最后一项“2n-1”错了，应该是“-(2n-3)·2n-2”，错误出现在相减后的最后一项.相减出错与乘公比出错类似，主要发生在最后一项，其主要原因是作差时最后一项与前面不同，运算路径发生了变化.而当运算路径发生变化时，中等生的出错率就会提高.

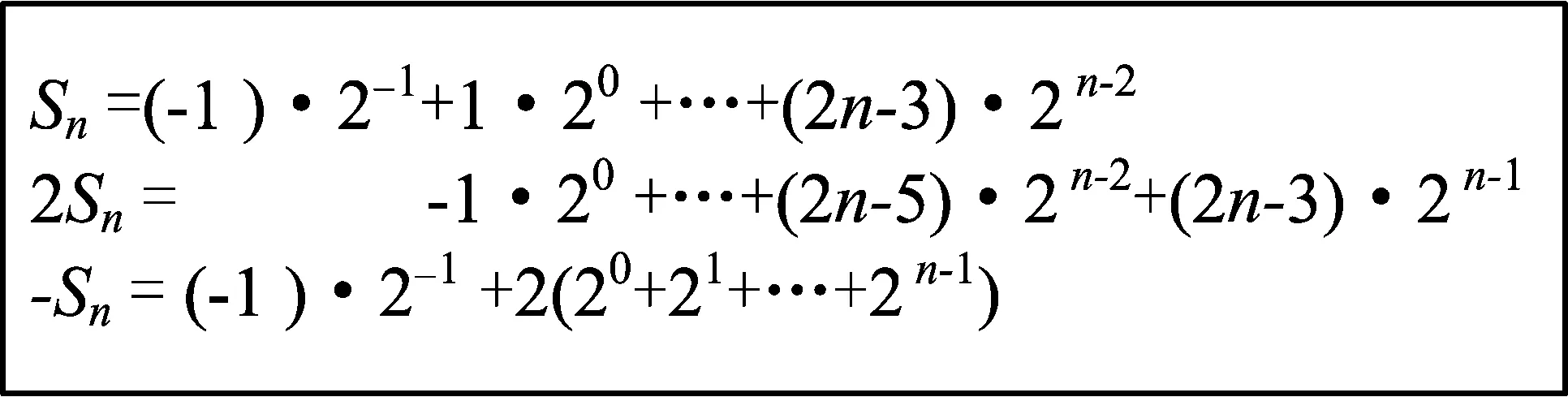
图3

3.4 相减后求和出错

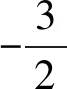
图4

3.5 相减后除以系数出错

相减求和正确，等式两边除以系数时出现的错误也较为常见.图5展现出来的过程都是对的，但是本题的解题目标是求“Sn”，这位学生只是求出了“Sn-2Sn”，即“-Sn”，忘记了除以系数“-1”导致出错，未能得到这一小题的满分“5分”，显现出解题过程中自我监控和目标意识的缺失.这种错误的原因是目标意识不足，“解题回顾”环节缺失.

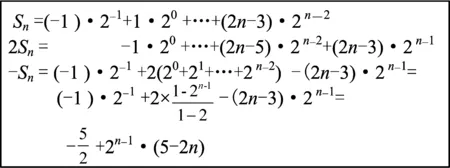
图5

3.6 最后结果的表达

《普通高中数学课程标准(2017年版)》(以下简称《新课标》)指出：要引导学生会用数学的语言表达世界[2].数学表达的目的之一是方便交流，这就需要有相对统一的格式要求，虽然教材上没有对错位相减法求和的结果给出统一规范要求，但如果借鉴等比数列的求和公式，笔者认为错位相减法求得的结果最好保留一项或两项，即A+(Bn+C)qn-1型，其中A,B,C为常数，q为等比数列的公比，这样更方便交流.

4 学生访谈、教师访谈

在考试结束后的一周内，笔者与部分学生和教师进行访谈.

4.1 学生访谈

考试答题纸返回到学生手中、公布各小题得分明细后的第二天，笔者对自己所在学校的一个普通班10名学生(这部分学生在第20题第2)小题中的得分为2～4分)进行了访谈，A代表笔者，S代表学生.

A：你认为你会做第20题的第2)小题吗？如果会，用什么方法做？

S1:会的，这是等差乘以等比数列的求和问题，应该用错位相减法.

(10名学生全都认为自己会做这种类型的题目.)

A：现在，你知道错在哪一步吗？

S2:现在我还是不知道自己错在哪里？

(10名学生中有7名这样回答.)

A：考试时做完第2)小题后，你能判断出自己的答案正确吗？

S3：我没有去判断，就接着写下一个小题了，但是下一道题目，也没有写出来.

(有8名学生这样回答.)

4.2 教师访谈

考试后的一周，笔者利用学期结束前最后一次组内教研活动的时间，对高一数学组的部分教师进行访谈，其中T代表接受访谈的教师.

A：关于数列求和中的错位相减法教学，请各位老师谈谈自己的体会和看法.

T1：见到等差乘以等比数列的求和问题，就应该想到可采用错位相减法求和，但有的学生还说是用裂项相消法，真是让我犯晕，这种学生怎么教？

T2：错位相减后，一定是对n-1项的等比数列求和，关于这一点，我强调了很多遍，学生还是出错.

T3：采用错位相减法求和，由于求得的结果各异，批卷费事，高考卷中一般不会出现这类题，因此不应过多复习，复习了也没有什么用.

5 中等生考试状态下“会而不对”现象的影响因素与应对策略

5.1 解题路径变化“点”较多容易导致“会而不对”现象

当解题路径变化“点”较多时，中等生更容易出现“会而不对”现象，这是“会而不对”现象产生的外在原因.错位相减法看似程序固定，容易操作，事实上，使用这种方法对数列求和时变化“点”较多：比如相减时的最后一项，与前面的项不同；相减后求和时，等比数列的项数问题；最后还需要除以系数，化简等等.这就要控制好解题过程中快与慢的“时段”，中等生在变化“点”处需谨慎而又缓慢前行.交通安全中常有提示：“事故多发于弯道、路口”“十个事故，九个快”，这两句警语对中等生解题也应有所借鉴.

5.2 短时记忆能力弱容易导致“会而不对”现象

短时记忆能力较弱是中等生的典型特征之一.记忆力弱更容易产生“会而不对”现象，这是“会而不对”现象形成的心理原因.从学生的视角上看，导致“会而不对”的主要影响因素是审题、计算和转化.如看错题目、误解题目、看错数字或符号等等，这些都与短时记忆的广度和准确性有密切的关系，也表现为学生的数学运算、逻辑推理、数学建模素养有缺失.错位相减法求和时，数字与字母混合，加、减、乘、除、乘方这5种运算混合，对短时记忆的准确性和广度要求较高，稍不留意就会导致错误.化“隐”为“显”，心算内容可视化，加密运算步骤可以有效减少“会而不对”现象.比如在写出Sn的展开式时，要求前3项和后2项具体，不可省略，教学实践表明这样做可以有效减少“错位相减”后最后一项出错的几率，也有利于“对相减后产生的等比数列”正确求和.同时对于常规问题，保证一定的训练次数，形成熟练度也是有必要的.

5.3 良好解题习惯的缺失容易导致“会而不对”现象

良好的解题习惯是提高解题效率和准确性的重要保障.波利亚提出解题的4个步骤：理解题意、拟定计划、执行计划、解决回顾[3].中等生面对一道感觉会做的题目，他们当然会完成前3个步骤，但是最后一个步骤“解题回顾”，被不少学生遗忘(访谈中10名学生有8名不知道自己错在哪里)，在考试状态下，更是如此.事实上，只要对最后的结果，取n=1，2，算出Sn，就可以立刻检查出错误.解一道题目切莫忘了“蓦然回首”这一步，即使在考试状态下也应如此.这比整张试卷做完后再回头检查效果要好得多.

6 减少中等生考试状态下“会而不对”现象的教学策略

减少中等生考试状态下“会而不对”现象，教师可以有所作为.结合教学实践、数据分析及教师访谈的结果，笔者提出以下4个教学策略，以减少中等生考试状态下的“会而不对”现象：

6.1 教师对数学内容理解的深入，更容易帮助学生减少“会而不对”现象

章建跃博士反复强调数学理解的重要性[4].准确而又深刻地理解数学内容是教好数学最重要的基础，与义务教育阶段的数学教学相比，这一点显得更为重要.如果教师对数学本身理解不深入，就无法准确地指导学生学习数学，与学生交流时也会捉襟见肘，不利于学生减少“会而不对”现象.对于等差乘以等比型的数列问题，从教师的访谈来看，还需要理解得更深刻一些，错位相减法并不是求解此类问题的唯一方法，裂项相消法也可以求解此类问题.访谈中T1提到“有的学生还说是用裂项相消法，真是让我犯晕，这种学生怎么教”，说明他可能不太了解“用裂项相消法也可以求解差比型数列的前n项和”.在数学解题研究中，加强对一类问题的多解研究是一线教师的必修课，也是深刻理解数学的一种手段.T2提到“错位相减后，一定是对n-1项的等比数列求和”，事实上错位相减后，可能是对n-1项的等比数列求和，也可能是对n项的等比数列求和，当等差数列的首项与公差相等时就会产生后一种情况.若教师对“差比型”数列进行一般性研究，即求出数列{(kn+b)qn}的前n项和，就会发现这一结论，同时也会发现结果相对统一的形式(一项或两项).对数学问题的一般化研究有利于更加全面地理解数学，进而更有效地与学生交流，帮助中等生减少“会而不对”现象.

6.2 改造出使学生更容易操作的数学，减少“会而不对”现象

张景中院士特别强调：既要“数学教育”,又要“教育数学”[5].改造数学使之更适宜于教学和学习，是教育数学的任务.张奠宙教授指出：教师的任务是把知识的学术形态转化为教育形态[6].不管是“改造数学”还是“把知识的学术形态转化为教育形态”，都需要教师创造性的劳动.怎样教，学生才更容易学会、做对、错误率小一些，中等生的“会而不对”现象少一些.这需要教师改造出更容易操作的数学.对于使用错位相减法求数列的和，一些教师作了有效的尝试,比如笔者所在学校的C教师要求学生：写出“Sn”的展开式时，要“前三后二(前面保留三项，后面保留二项)”；乘公比错位时，要“向后错位，补0对齐再相减”等，这样可以有效提高相减时的准确性，减少“会而不对”现象的发生.通过数据比较,我们发现：C教师所教班级在此题的得分上显著高于同层次其他班级.改造数学，使之容易操作，提前预防错误发生，让学生有序地展开运算，就是培养学生数学运算素养的过程.

6.3 加强试题研究，做好考试指导,可以有效减少“会而不对”现象

教师要加强高考试题研究，通过研究高考试题明确考试方向，指导教学.访谈中T3提到“采用错位相减法求和，由于求得的结果各异，批卷费事，因此高考卷中一般不会出现这类题”，表明T3缺少对高考题的了解和研究.事实上，近5年的高考试题中每年均有“差比”型数列求和(一般使用错位相减法)的考题.比如2014年全国新课标卷Ⅰ文科第17题、2015年湖北省数学高考理科第18题、2016年山东省数学高考理科第18题、2017年天津市数学高考文科第18题、2018年浙江省数学高考第20题等.此外，关于错位相减法求得的结果，只要教师对学生稍加指导,保留A+(Bn+C)qn-1型，求得的结果也不会形态各异.这样的指导让学生的书写更易得分，同时也方便了交流.

6.4 给学生足够的“悟”的时间，可以有效减少“会而不对”现象

《新课标》强调：提倡独立思考、自主学习、合作交流等多种学习方式[2]，需要注意“独立思考”是摆在第一位的，这也是数学学科自身的特征之一.没有经过“独立思考”的合作交流(小组讨论),虽然有时候看起来学生的参与度很高，但是通常是肤浅的，也是低效的.在错位相减法教学时，除了教师的启发、讲解外，还需要给予学生自主练习、独立体悟的时间，让学生悟出“错位相减法”的解题流程和注意点.“悟”首先是学生个人独立的思考.有问题就立刻组织学生展开讨论，事实上剥夺了学生自主思考的时间和空间.学生拥有足够的“悟”的时间，就更容易发现适合自己的解决问题的方法，形成自己的解题模块，可以有效地减少“会而不对”现象.