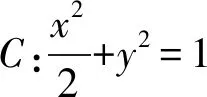一道解析几何试题的背景揭示及变式研究
(黄陂区第一中学盘龙校区,湖北 武汉 430312)
●孔 峰
(武汉市教育科学研究院,湖北 武汉 430032)
每年全国各地的高三调考试卷中,总有一些亮眼的试题,它们独具匠心,延伸性、代表性和示范性颇佳,对这些试题进行深入的探索、延伸和拓展,挖掘其潜在的价值,既能呈现丰富多彩的教学内容,激发学生的学习兴趣,又有利于拓展想象力,提高思维的灵活性与深刻性[1].2019年湖北省武汉市高三二月调考理科解析几何试题就是其中一例.

1)求椭圆Γ的方程;
2)过点P(1,0)作直线交椭圆于点A,B,点Q为平面上一点,QA,QB,QP的斜率分别为k1,k2,k0,且k1+k2=2k0,问:点Q是否在某条定直线上?
(2019年湖北省武汉市高三二月调考理科试题第20题)
做完此题,笔者意犹未尽,总觉得有某些一般性的结论蕴含其中,经过一番思考和研究,得到如下9个更具一般性的结论,现草拟成文,与同仁们分享.
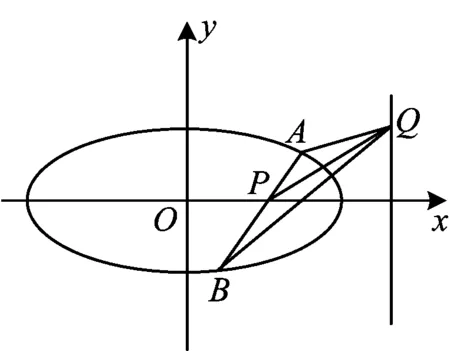
图1
1 从特殊到一般的拓展

证明设A(x1,y1),B(x2,y2),Q(x0,y0).
1)若直线AB与x轴不重合,不妨设直线AB的方程为x=my+t,代入椭圆方程,整理得
(a2+b2m2)y2+2b2mty+b2(t2-a2)=0.
由|t|
由k1+k2=2k0得
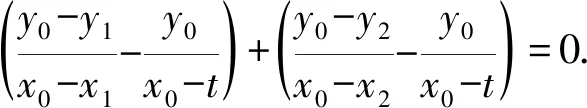
(1)


由-x0+t+my0不恒为0,知式(1)⟺

y1(x0-my2-t)+y2(x0-my1-t)=0⟺
(x0-t)(y1+y2)-2my1y2=0⟺
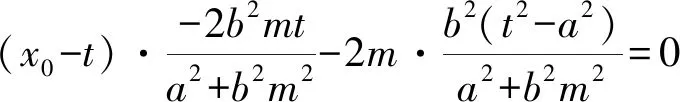
2b2mtx0=2ma2,
因此




1)若直线AB与x轴不重合,不妨设直线AB的方程为x=my+t,代入椭圆方程,整理得
(a2+b2m2)y2+2b2mty+b2(t2-a2)=0.
由|t|
k1+k2-2k0=(k1-k0)+(k2-k0)=
(2)

故式(2)为0,即k1+k2=2k0.
2)若直线AB与x轴重合,此时k1=k2=k0=0,满足k1+k2=2k0.
综合1),2)可知k1+k2=2k0.


1)若直线AB与x轴不重合,不妨设直线AB的方程为x=my+λ(其中|λ| (a2+b2m2)y2+2b2mλy+b2(λ2-a2)=0. 由|λ|<0知Δ>0,则 k1+k2-2k0=(k1-k0)+(k2-k0)= (3) 2)若直线AB与x轴重合,显然直线AB过点P(t,0). 综合1),2)可知直线AB过定点P(t,0). 对于结论1,若k1+k2=0,则k0=0,此时点Q在x轴上,于是得到如下结论: 对于结论2,若点Q在x轴上时,由k0=0知k1+k2=0,即直线AQ与BQ的斜率互为相反数,则∠AQP=∠BQP,即: 对于结论3,若点Q在x轴上,由k0=0知k1+k2=0,即直线AQ与BQ的斜率互为相反数,则P为定点,其坐标为(t,0),得: 以上结论1~6均可以类比到双曲线和抛物线中,限于篇幅,仅对抛物线作出说明,证明从略. 结论7已知抛物线y2=2px(其中p>0),点P(t,0)(其中t>0),过点P的动弦交抛物线于点A,B,点Q为平面上一点,QA,QB,QP的斜率分别为k1,k2,k0,且k1+k2=2k0,则点Q的轨迹为直线x=-t. 结论8已知抛物线y2=2px(其中p>0),点P(t,0)(其中t>0),过点P的动弦交抛物线于点A,B,若Q为直线x=-t上任一点,QA,QB,QP的斜率分别为k1,k2,k0,则k1+k2=2k0. 结论9已知抛物线y2=2px(其中p>0)的动弦AB交对称轴于点P,点Q为直线x=-t上任一点,QA,QB,QP的斜率分别为k1,k2,k0,若k1+k2=2k0,则P(t,0). 回顾近几年全国各地的高考试题,从中发现了许多熟悉的“身影”,不少试题便是以上述结论为背景命制,细心品味,让人有种“会当凌绝顶,一览众山小”的愉悦. 以结论5为命题背景的试题有: 1)略. 2)设O为坐标原点,证明:∠OMA=∠OMB. (2018年全国数学高考卷Ⅰ理科试题第20题) 以结论6为命题背景的试题有: 1)求椭圆E的方程. (2015年四川省数学高考理科试题第20题) 例4已知动圆过定点A(4,0),且在y轴上截得的弦MN长为8. 1)求动圆圆心的轨迹C的方程; 2)已知点B(-1,0),设不垂直于x轴的直线l与轨迹C交于两个不同的点P,Q,若x轴是∠PBQ的平分线,证明:直线l过定点. (2013年陕西省数学高考理科试题第20题) 1)略. 2)设O为坐标原点,点B与点A关于x轴对称,直线PB交x轴于点N,问:y轴上是否存在点Q使得∠OQM=∠ONQ?若存在,求点Q坐标;若不存在,请说明理由. (2015年北京市数学高考理科试题第19题) 以结论8的特殊情形为命题背景的试题有: 例6设抛物线C:y2=2x,点A(2,0),B(-2,0),过点A的直线l与抛物线C交于点M,N. 1)略. 2)证明:∠ABM=∠ABN. (2018年全国数学高考卷Ⅰ文科试题第20题) 以结论9的特殊情形为命题背景的试题有: 1)略. 2)问:在y轴上是否存在点P,使得当k变化时,总有∠OPM=∠OPN?请说明理由. (2015年全国数学高考卷Ⅰ理科试题第20题) 高考试题讲究“常考常新,推陈出新”,以上结论在高考中还有一些没有出现,但为以后的试题命制提供了广阔的空间. 通过对例1的拓展研究以及与高考试题的纵横联系,我们充分感受到了数学探究的乐趣.其实,许多高考和调考试题都凝结了命题专家巨大的智慧和心血,它们有的背景深刻,有的内涵丰富,有的立意高远,有的创意新颖,在研究的过程中,可以进一步领悟解题方法和思想,领悟问题的深层次联系,解题能力和思维品质能向更深、更高的层次发展和升华[3]!


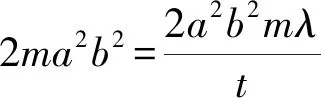
2 从一般到特殊的发现



3 结论的横向类比
4 高考真题再现