细化课堂教学目标 促进数学知识落实——两节公开课的实录与反思
(临安中学,浙江 杭州 311300)
●凌学芳
(吴兴高级中学,浙江 湖州 313000)
●赵孝华
(黄岩中学,浙江 台州 318020)
1 问题的提出
教学目标是关于教学将使学生发生何种变化的明确表述,是指在教学活动中所期待得到的学生的学习结果[1].在教学过程中,教学目标起着十分重要的作用,教学活动以教学目标为导向,且始终围绕实现教学目标而进行.
关于数学课堂教学目标的制定,章建跃博士多次在教育会议上提出,数学课堂教学目标首先要分清楚3个层次:课程目标、单元目标、课堂教学目标,其中课堂教学目标要向3个方面努力,即具体化、可操作、可检测,学生在经历了课堂教学后,能看到其课前、课后的变化[2].
课堂教学目标的具体化、可操作、可检测,明确了教师在制定课堂教学目标时需要达到的要求.课堂教学目标是教师实施课堂教学的指挥棒,它让教师知道需要做什么、什么时候做、怎么做.
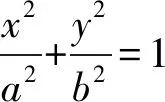
独立样本四格表的χ2检验步骤:1)提出假设;2)计算卡方值;3)统计决断.通过计算所得数据的χ2值,笔者发现细化该知识点的课堂教学目标进行教学与学生对该知识的掌握具有明显的相关性,相关系数高达31.28.在此基础上,笔者通过查询资料,就“如何通过细化课堂教学目标,促进数学课堂知识落实”得到了一些初步结论.
2 课堂教学目标与课堂实录及其分析
在两节公开课以及公开课前一天的教师试讲课及课后通过讨论调整课堂教学目标后的3节关于推导标准方程的课中,均呈现了授课教师的课堂教学目标,相关实录片断如下.
2.1 试讲课与公开课的课堂教学目标与课堂实录
试讲课与公开课1、公开课2的授课教师未对课堂教学目标进行细化处理.
在试讲课与公开课1的教案中呈现的课堂教学目标是:1)通过讲授,简单了解圆锥曲线的产生背景.探究椭圆的概念,经历从具体到一般的数学抽象过程,学会用归纳的方法提炼数学概念、掌握概念的本质;学生通过合作探究,在教师的引导下,对椭圆的定义进一步精细,形成扎实严谨的数学学习风格.2)进一步深入领会求动点轨迹方程的一般方法.在化简与探究中体会知识形成过程中的乐趣和艰辛,进而培养学生乐学、苦学的精神.
公开课2的教案中呈现的教学目标是:在理解椭圆定义的基础上,掌握椭圆标准方程的推导过程,并最终得到椭圆的标准方程;学会利用条件求椭圆的标准方程;能用标准方程判断椭圆.其目标解析是:在椭圆定义的获知和归纳中,进一步渗透数形结合的数学思想方法;通过椭圆标准方程的推导过程,进一步领会求动点轨迹方程的坐标化思想,同时体会含有两个根式方程的化简思路.
这几个教案都没有对“什么是椭圆方程”这一教学目标进行细化.在此教学目标指导下,教师的课堂教学实录片断如下:
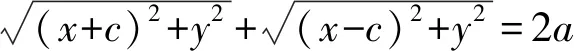
(学生动手化简整理,教师巡视,手机拍摄并展示学生化简的成果.)
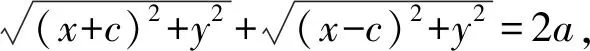
2x2+2y2+2c2+
其中(x2+y2+c2-2cx)(x2+y2+c2+2cx)=
(x2+y2+c2)2-4c2x2=
(y2+c2)2+2x2(y2+c2)+(x2)2-4c2x2=
(y2+c2)2+x2(2y2+x2-2c2).
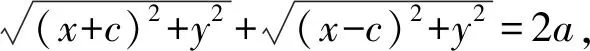
从而(x+c)2+y2=
即
于是
即
a4-2a2xc+x2c2=a2(x2-2xc+c2+y2),
整理得
(a2-c2)x2+a2y2=a2(a2-c2),
故
教师未对学生给出的等式进行说明,没有指出以下6个等式都可以是椭圆的方程.
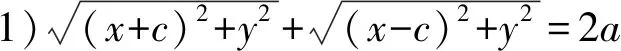

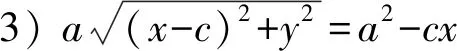
4) (a2-c2)x2+a2y2=a2(a2-c2)(其中a>c>0);
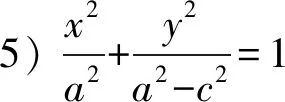
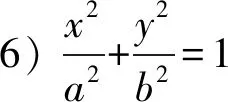
2.2 试讲课与公开课课堂教学目标与教学过程的分析
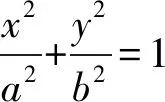
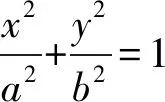
2.3 调整后的课堂教学目标与课堂实录片断
根据《普通高中数学课程标准(实验)》及《普通高中数学课程标准(2017年版)》中对人教版《数学(选修2-1)》第2.2节“椭圆”的要求,椭圆标准方程的课堂教学目标是“经历从具体情境中抽象出椭圆的过程,掌握椭圆的定义、标准方程及简单几何性质”[3].
学情分析学生具有较好的数学基础,能对代数式进行化简整理,能进行简单地归纳总结.学生刚学习完“曲线与方程”的内容,能理解什么是椭圆方程的具体要求,掌握某方程是椭圆方程必须要说明纯粹性与完备性.
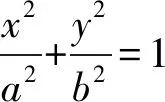
在此课堂教学目标的指导下,两位教师上了3节课.其中一节课的课堂教学片断实录如下:
(学生动手化简整理,教师巡视,并用手机拍摄学生化简成果.)
师:同学们基本上分成两派:一派是直接平方化简,大家可以看到,平方后的工作很困难;另一派是移项后再平方.
(教师展示“另一派”学生的成果,过程略.)
师:非常漂亮!最后的方程是椭圆方程吗?还需要做什么工作?
(教师展示如下化简过程.)
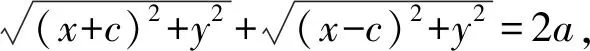
再平方,整理得
(a2-c2)x2+a2y2=a2(a2-c2),
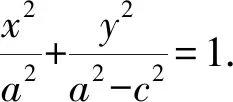
生(众):需要检验完备性!
师:那大家看看,上述化简过程具有完备性吗?
生(众):具有完备性.
师:那么大家思考,这些等式是否都是椭圆的方程?
生(众):是的.
师:该椭圆方程表示的椭圆焦点在哪个轴上?a,b,c满足什么关系?你能在图中找出长度分别是a,b,c的线段吗?
生(众):|PF1|=|PF2|=a,|F1O|=|F2O|=c.
师:非常好!由此我们可以知道|PO|的平方就是b.
师:令a2-c2=b2,得到方程
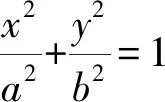
这几节课中,授课教师明确指出了哪些是椭圆的方程、哪些是椭圆的标准方程.
3 针对椭圆方程掌握情况的调查结果进行分析
调查问卷共两个题目(如下例1与例2),例1的目的是调查学生对椭圆方程的认识,其中等式1),3),6)是椭圆方程的重要形式,选中等式3)的学生可以认为他对“什么是椭圆方程”有较深刻的理解和认识;例2的目的是区分课堂教学目标是否细化到“说明标准椭圆方程的完备性,推导过程中的每个等式都是椭圆的方程”.
例1你认为下列等式哪个是椭圆的方程:
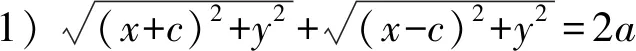
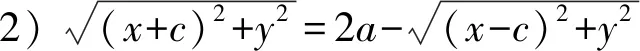
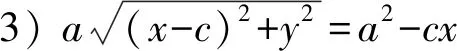
4) (a2-c2)x2+a2y2=a2(a2-c2)(其中a>c>0);
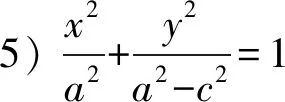
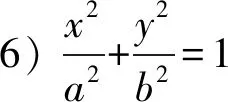
其中,你认为是的有______(认为是的都填上).
例2课堂上老师是否有讲解哪些是椭圆方程
( )
A.有 B.无
调查问卷在两类班级发放(其中一类班级3个,是公开课授课班级;另一类班级3个,是课堂教学目标调整后新授课的班级),共发出问卷198份,这6个班级都是在第一课时结束、第二课时上课前进行调查.回收问卷198份,其中废卷(没有选择或例2写有C,D等选项的是废卷)27份.
在调查问卷中,方程3)是从定义到标准方程转化过程中的核心,也是对椭圆第二定义学习的一个重要方程,因此可以认为选择方程3)的学生已经掌握了椭圆方程的定义,没有选择方程3)的学生只掌握了椭圆的标准方程.
表1 两类班级学生椭圆方程掌握人数统计

掌握的人数没有掌握的人数合计细化教学目标后771289细化教学目标前384482合计11556171
1)提出假设.H0:细化教学目标与椭圆方程掌握无本质差异;H1:细化教学目标与椭圆方程掌握有本质差异.
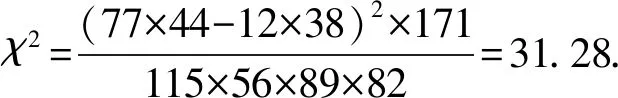
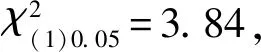
4 课堂教学目标的细化
对于什么是良好的教学目标,文献[4]指出:能清晰说明总结性学习结果;对学生有明确的学习要求;教学目标制定需要进行需求评估和问题鉴别;目标是通过教学达成的,而非情感传达等其他途径.
课堂教学目标的细化需要考虑4个方面:课程教学目标的要求、章节教学目标的要求、学生学情分析和教学目标解析.下面以“椭圆及其标准方程(第一课时)”为例进行说明.
4.1 教学内容及其分析(体现课程教学目标和章节教学目标)
1)内容:椭圆的产生与定义,椭圆方程的推导,能求椭圆方程.
2)地位和作用:平面解析几何是用代数方法解决平面几何问题,通过坐标化的方法建立代数与几何的联系.椭圆是3类圆锥曲线的代表,“椭圆及其标准方程(第一课时)”是在学习了直线与圆、曲线与方程之后,学习3类圆锥曲线的起始内容.教材以椭圆为重点说明了求曲线方程及利用曲线方程研究曲线的一般方法,再用这些方法研究双曲线与抛物线,因此本节内容具有承上启下的作用.
3)思想方法:坐标化思想.
4)知识类型:概念课.
5)教学重点:椭圆的定义,椭圆的标准方程及其推导.
4.2 学情分析
本节课的授课对象是重点高中的学生,具有较好的数学基础,能对代数式进行合理地化简与整理,能对简单结论进行归纳分析.
4.3 教学目标解析
1)动手画椭圆,根据两定点间距离与距离和之间的关系理解椭圆的定义;
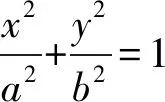
3)借助简单练习,强化椭圆两个不同标准方程的差异,能求椭圆的标准方程.
细化课堂教学目标可以让课堂教学目标对教师的课堂授课具有切实的指导作用,可以让数学课堂教学目标的“具体化”“可操作”“可检测”得到真正实现.

