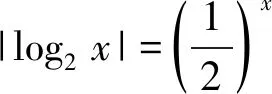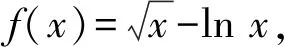用数形结合求解一道函数零点问题的反思
(杭州第二中学,浙江 杭州 310053)
研究函数零点的过程中,经常会利用函数图像,即数形结合求解问题.画出的草图不够精确,一般不影响问题的解决,但与问题紧密相关的位置关系不能粗略判断,需要从数的角度来细致地分析、计算,否则容易出现错误.正如著名数学家华罗庚先生所说:数缺形时少直观,形少数时难入微.利用数形结合思想方法求解函数问题时,要注意数与形的互助,从而准确求解问题.
笔者先从高三复习中的一道测试题说起,这个题目看似简单,实则不易,易漏易错.
1 试题呈现及解法分析

分析此题中函数f(x)比较复杂,直接探索比较麻烦,不难想到可把原问题等价转化为方程根的问题,从而进一步转化为函数图像公共点的问题.
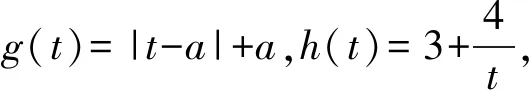

图1 图2 图3

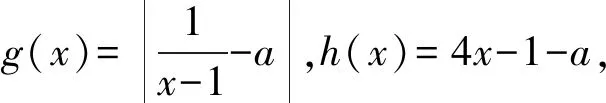
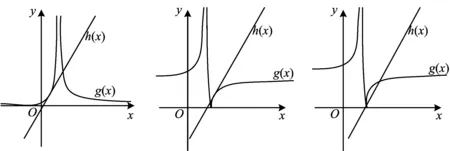
图4 图5 图6
比较两种解法,同样是数形结合,但难易程度明显不一样:前者通过换元,转化为研究含参数的“V”形图像与确定的曲线的位置关系;后者研究含绝对值的曲线与一条直线的位置关系,并且含有参数,情况复杂很多,需要注意的地方较多,而且有些关键的位置关系需要从数的角度来确定,否则很容易出错.
如图7,手工画草图时,完全有可能把(0,1)区间上g(x)的图像(此时a=-1)画成曲线m,就多了一种情况,但它是不对的!表面上看,m与原图的区别是曲线“凸出”的程度不一样,本质在于原点右侧g(x)切线的斜率,若比h(x)的斜率“4”还大,则这又是一种符合题意的情况.但事实上,不难算得g′(0+)=1<4,此时g(x)的图像与h(x)的图像会有3个不同的公共点.其中g′(0+)表示g(x)在0右侧的导数值.
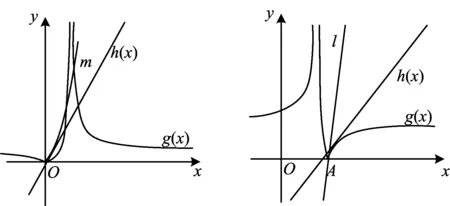
图7 图8
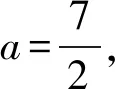
做完这道题,笔者恍然大悟,不是学生没有数形结合的意识,也不是不会用数形结合,而是数形结合之后,问题可能还是比较复杂,很容易出错、漏解!笔者开始反思用数形结合解题的过程,想到了如下两点启示.
2 两点启示
2.1 要重视从数的角度研究关键的形
在例1的解法2中,从数的角度分析计算,解决了由于草图不够精确带来的疑难[2],此类型的问题还有很多.
例2已知函数f(x)=(x2+x-4)e-x-ax,若函数f(x)有两个不同的极值点,求实数a的取值范围.
分析原问题等价于f′(x)=e-x(-x2+x+5)-a有两个变号零点(零点附近左右两边的函数值异号),等价于方程e-x(-x2+x+5)=a的根的问题,进一步等价于g(x)=e-x(-x2+x+5)与y=a有两个交点.
因为g′(x)=e-x(x2-3x-4)=e-x(x+1)(x-4),所以g(x)在(-∞,-1)上单调递增,在(-1,4)上单调递减,在(4,+∞)上单调递增,并且当x→+∞时,g(x)→0;当x→-∞时,g(x)→-∞,画出图像如图9所示,易得a∈[0,3e).

图9 图10
评注阅卷过程中,有很多学生认为实数a不存在,经过了解,他们都是把图像画成了如图10所示的情况.很明显,这是忽视了求极限而画错了函数图像,从而导致求解错误.
例3若函数f(x)=|2x-2|-b有两个零点,则实数b的取值范围是______.

图11
分析原问题等价于|2x-2|=b有两个不等实根,即g(x)=|2x-2|与y=b有两个不同的公共点,画出图像如图11所示,即得0 例1的解法1通过换元,使得所要研究的函数变得容易把握,从而能迅速、准确地求解.常见的代数变形除了换元之外,还有方程和不等式变形.举例如下: 例4求函数f(x)=2x|log2x|-1的零点的个数. 分析此函数图像的草图不容易画出来,需要转化. 图12 评注通过代数变形将原问题转化为两个适当的函数图像的公共点问题,使得数形结合的应用水到渠成. 1)略; 2)证明:对于任意的k>0,直线y=kx+a与y=f(x)有唯一的公共点. (2018年浙江省数学高考试题第22题) 分析直接画y=kx+a与y=f(x)的函数图像,发现操作起来不太容易,于是笔者尝试等价变形,分离出k. 从而h(x)在(0,16)上单调递增,在(16,+∞)上单调递减.又a≤3-4ln 2,得 h(x)≤h(16)=4ln 2-3+a≤0, 于是g(x)在(0,+∞)上单调递减.又当x→0+时,g(x)→+∞;当x→+∞时,g(x)→0,故g(x)的值域为(0,+∞). 评注本题属于难题,但作了合适的代数变形后,转化成了两个“好”(容易研究的)函数的图像公共点问题,降低了问题的难度,显示出数形结合强大的威力. 总之,在函数零点问题中:一方面,以形助数,让问题直观地表达出来,降低求解的难度;另一方面,以数定形,通过分析函数性质、定量计算,确定函数图像关键的位置关系.在实际问题中,通过等价代数变形,把问题当中的函数转化为“好”函数,有助于简化问题,提高使用数形结合解题的效率.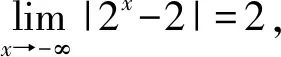
2.2 善于利用代数变形,构造适当的函数,让数形结合事半功倍