教之道在于度 学之道在于悟——从一堂高三数学探究活动课说起

(辅仁高级中学,江苏 无锡 214123)

高三数学复习课往往是学生在教师的引领下对已学知识进行系统化和网络化建构，对概念本质进行深刻性和广泛性理解，对数学方法进行合理性和灵活性应用，对数学问题的本质进行深度探究和再升华的过程，是实现学生的知识生长、思维发展和能力提升的主战场．基于此，许多教师会产生这样的疑问：什么样的课堂是复习课的好课堂，什么样的课堂有利于学生的思维发展，什么样的课堂有利于提高学生的数学成绩，什么样的课堂有利于培养学生的创新精神和实践能力，什么样的课堂有利于培养学生的数学核心素养[1]？

笔者认为，能力扎根于学生的经验，来自于对问题的发现、分析和理解的过程，伴随着对已有知识和经验的自我改造、重组与更新．高三数学复习课教学应从学生的学情出发，组织学生进行深度学习[2]，应注重学生的主动参与、积极建构、合作交流、多角度审视和深层次探究，以及教师的合理引导、适度启发和恰到好处的“点睛”；不应是走马观花式的表层学习、浅层学习、机械学习和“知其然而不知其所以然”的模仿式学习．下面，笔者以一堂高三数学深度理解的活动课为例，探索高三数学复习课的“教”“学”之道，旨在抛砖引玉．

1 问题呈现

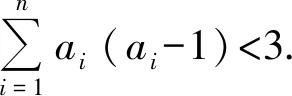
2 组织探究活动

对问题进行多角度、深层次探究能够有效地帮助学生自主构建数列的认知网络，获得解决问题的方法，从而揭示问题的本质，通过联想、类比能将陌生的、复杂的问题转化成熟悉的、简单的问题来处理[3]，通过比较各种方法的优劣，可以有效地训练学生的思维，培养学生的数学核心素养，提高学生分析问题和解决问题的能力．

2．1 他山之石可攻玉

证法1当i=1,2,3时,

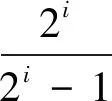
证法2当i≥2时，

此时学生和教师一起进行总结和点评：前面的学生处理得很好，尽管失败了，但失败中蕴含着成功的经验和启发作用．学生们一定想知道：上面的两种方法是如何想到的，为什么这样想，问题解决的本质和关键是什么？实际上，解决问题的本质是如何求出目标中各项的和或适当放大后的和，对这个“适当”我们还有别的办法吗？

2．2 似曾相识燕归来

第三小组的学生非常激动，但激动之余他们也遇到了和生1同样的困境：

有了证法1的经验，他们获得了成功，得到证法3．

证法3当i=1,2,3时,

尽管证法3比较巧妙，但很多学生仍然不满意，认为还是比较复杂.于是第四小组的生4提出,若放大的幅度小一些，会和证法2一样，没有必要从第4项开始放大，经本组学生的共同努力得到了更为巧妙的证法．

证法4当i≥2时，

2．3 柳暗花明又一村

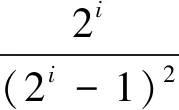
令全体师生拍案叫绝．

证法5当i≥2时，

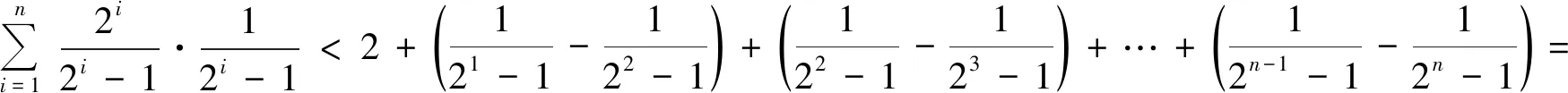
正当大家沉浸在成功的喜悦中时，平时不善言谈且成绩一般的第六小组生7和同桌生8同时站了起来，害羞地说：“受二项式定理的启发，我们得到了又一种证法，不过方法有些复杂”．此刻，大家用羡慕的目光欣赏着两位学生与众不同的“柳暗花明又一村”的喜人证法．

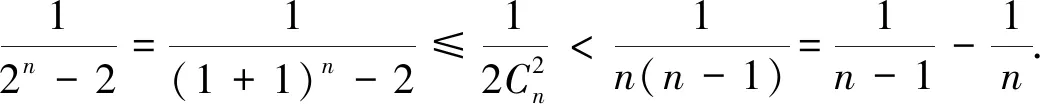
这时，伴随着数列不等式的各种放缩方法的精彩展现，问题得到深层次、彻底的解决.学生意犹未尽，收获满满,下课铃响了，全班响起了热烈的掌声．

3 几个关键环节的评析

从生1的联想可以看出，学生的思维很活跃，具有较强的开放性、发散性和创造性.尽管生1的念头没有达到预期的效果，但大家的收获颇多，他的思路为证法1和证法2的获得埋下了伏笔，提供了保证．

第三小组的集体智慧是证法3和证法4的关键，同时更是巧妙证法5的思想源泉；而生7和生8的奇思妙想是证法6的关键，他们是怎样想到的？这是学习者对问题本质的深刻理解、相关知识的广泛联想和问题内涵与外延的深刻感悟的成果.尽管处理的技巧性较强，但他们敏锐的观察力和团队合作的精神，足以让大家钦佩．

整个探究活动的过程，教师不仅仅是在传道、授业、解惑，更是在作为配角和学生一起去观察、联想和探究，是在恰当的时候给予恰当的点拨和点睛．尽管本节课只解决了一个问题，但学生获得了解决一类问题的解法，从某种意义上讲，解题教学应追求“质”而不是“量”，课堂也不是仅仅将知识和方法强行灌输给学生，而是以知识为载体教会学生思考，让学生学会提出问题、分析问题和解决问题，实现学生知识的生长和能力的提升．

4 对教学的思考

教的悲哀是替代，学的悲哀是依赖．在教学活动中，教师不应把现成的结论和方法直接告诉学生，而应让学生自己去对学习的对象进行探索、研究，自己去获得．教师应多在学生思维的“最近发展区”设置有一定思维价值且能激发学生自主、合作、探究的问题或问题串；应多创设问题质疑的情境，并精心对待学生的每一个想法和念头；应在教师的引导下放手让学生自主探究、合作交流和大胆猜想[4]．这样，学生既能深化对概念与规律的认识与理解、完善认知结构，又能获得问题研究的方法和成果、提升数学素养、实现长效发展．

数学探究活动是培养学生创新精神和实践能力的重要途径，它有利于培养学生对数学学习的情感和态度，增强学习的自信心和克服困难的意志力，有利于加深学生对所学知识的理解，掌握解决问题的方法和策略，提高解决问题的能力．因此，在教学过程中，应让学生经常参与探究活动，并在探究的过程中激发他们的主动性和自觉性，引导他们自己总结、概括探究的方法，交流、反思探究的成果，从中体会和感悟数学学习的策略和途径．

教之道在于“度”，学之道在于“悟”．课堂教学是教与学的双边活动，教的秘诀在于适度，度就是恰到好处，就是能在恰当的时间和结点给予恰当的启发和帮助；学的真谛在于悟，悟就是学生的独立思考，是用心感悟，是自主构建，是反思提升，是高效的学习方法．在数学教学过程中，教师应对“教”和“学”的度精准把握，努力做到合情合理、收放有度．

教育的视野决定了教育的品位．高三的数学复习应立足于以学生的发展为本、以育人为目的，要基于学生的知识经验和实践经历，设计具有思考价值和挑战性的问题系列，组织兴趣盎然的探究活动，促使学生领悟知识方法、内化活动经验、发展学习能力.教师应注重“启、诱、导、探、悟”，在问题解决的突破口、转换的方向、化归的手段及运算的变形上，通过学生尝试分析、感悟领会，进而转化为自身的能力，使学生“悟得到、想得通、算得出、留得住、用得上”，实现真正意义上的深度学习．