渗透数学思想方法，灵动学生思维

⦿邹珍珠

《数学课程标准》(2011版)提出：“学生通过学习，能够获得适应未来社会生活和进一步发展所必需的重要数学知识以及基本的数学思想方法。”可见，数学思想对学生的后续发展具有着重要的意义，是数学教师不能忽视的重要内容。在以往的课堂教学中，很多教师将知识“倾囊相授”给学生，只注重技能的训练，而忽视知识背后数学思想的渗透，致使学生不能透彻地掌握所学知识。因此，教师应注意扭转这一局面，在课堂教学的过程中，应有意识地向学生渗透知识背后的数学思想，深化学生对所学知识的理解，建构完整的知识体系，提升学生的数学素养，实现可持续发展。

一、渗透转化思想，促进内化

转化是最基本的数学思想，也是学生进行研究和解决数学问题的有效途径。数学知识有着很强的系统性和逻辑性，前后的知识点有着非常密切的关联性，在学习的过程中，应激发学生运用已有的生活经验和知识基础，突破所学新知，完善良好的知识体系。为了加快新知内化的历程，教师应为学生搭建新旧联系的桥梁，运用知识间的联系，对新知进行迁移，将所学知识融入到原有的知识体系中，提升学生自主学习的能力。

在教学多边形的内角和时，教师首先在屏幕上出示了四边形、五边形、六边形……然后让学生们思考，它们的内角和是多少？学生们一时语塞，没有办法回答。教师让学生选择其中的一个图形进行探索，因为学生已经有三角形内角和的探索经验，所以都觉得应该从四边形入手。有的学生用量角器，分别测量出每个内角的度数，然后进行相加。也有学生将四边形的四个内角剪下来，然后拼在一起，看可以拼成什么图形。但学生们很快发现了问题，因为操作的原因，存有一定的误差，大家的结论不一，怎么办呢？很快有学生想到，可以连接四边形的一条对角线，将它分成两个三角形，一个三角形的内角和是180度，两个三角形的内角和就是360度。这样的转化方法，得到了大家的肯定，并运用到了五边形、六边形内角和的探索中。

上述案例，教师立足学生已有的知识经验，进行新知探索，让学生在探索中发现问题、分析问题，进而想到运用转化的策略，实现新知的内化，提升了课堂教学效益。

二、数形结合思想，化难为易

数与形是数学中的基本元素，也是人们学习数学、研究数学的有效入手。数形结合是一种重要的数学思想，也是解决问题的有效策略。学生因为年龄的原因，他们的抽象思维能力还不发达，更多的时候仍以形象思维为主。在学习的过程中，经常会被知识的表面现象所迷惑，无法掌握知识的本质。在解题的过程中，会出现这样或者那样的问题，此时教师就可以向学生渗透数形结合的思想，将抽象的文字信息，转变成直观、形象的图形，让学生对照所画的图形，探寻有效的解题思路，提高学习的效果。

在教学长方形和正方形的周长后，教师出示了这样的问题：“用2个边长6分米的正方形，拼成一个长方形，所拼长方形的周长是多少？”题目出示后，发现绝大多数学生的结果是48分米，究其原因，是他们先算出一个正方形的周长，在此基础上，然后乘2。显然，学生们没有能够把握这道题目的内涵，陷入了思维定势。面对这种情况，教师没有直接告知学生正确的算法，而是引导学生根据题目中的条件，画出了图形，然后对照所画的图形，探寻有效的解题思路。经历了这样的过程后，学生们发现原先的算法是不正确的，应该先判断出所拼长方形的长(12分米)和宽(6分米)，然后列算式，计算出了所拼长方形的周长，得出了正确的结论。

上述案例，在学生的思维陷入困顿之时，教师没有“全盘托出”给学生，而是引导学生，将复杂的数量关系，变成直观、形象的图形，借助图形理清了解题思路，强化了理解。

三、渗透比较思想，掌握本质

比较是一种非常重要的数学思想，世界上的很多知识人们都是通过比较所获取。苏教版数学课本安排了很多的性质、规律、公式等内容，这样内容形式相似、内容相关，学生难以透彻、深入地理解。在课堂教学的过程中，教师应以学生既有的数学知识为依托，设计比较活动，让学生通过对知识点的比较，对知识点进行有效的分析、推理以及概括等，从而帮助学生牢固而深刻地掌握所学知识，延伸学生学习的深度、厚度和广度，最大化课堂教学效益。

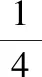
上述案例，教师巧妙渗透比较思想，设计了带有比较性质的练习，加强了学生对“分率”与“数量”的辨析，提升了学生分析问题、解决问题的能力，提升了课堂教学效果。

总之，数学思想是数学知识的精华，也是提升学生核心素养的有效途径。在课堂教学的过程中，教师应研读教材，精心挖掘知识背后的数学思想，巧妙地渗透到学生的学习活动中，提升学生的思考力和创造力，灵动学生的思维，从而让数学课堂更加的精彩！