立足母题，展开联想——以一道“重心”题的解题为例

谷 一

进入高三以来，老师一直要求我们多做题、做好题、多思考、多联想.能够通过解一道题，联想到多种方法和类似的题，有助于开拓我们的思维.

前几天老师布置我们做一道关于重心的题，题目是这样的：

如图1，若点G为△ABC的重心，且AG⊥BG，则sinC的最大值为________.

图1

拿到题目后我开始思考：点G为△ABC的重心，就有，又有.好！我就以与为基底处理.

解设，则-a-b，a·b＝0.

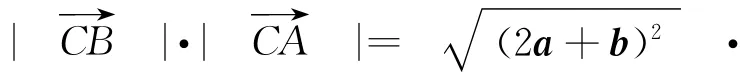
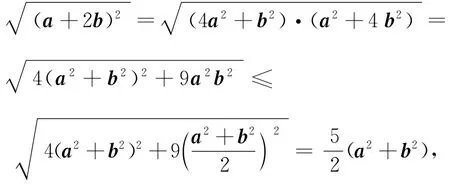
老师看了我的做法后，表示认可.却又提出了一个问题：本题中，三角形三条边又有怎样的关系呢？

我思考着：如果能够用边BC，AC，AB的长度表示出BC，AC边上的中线的长度，那么就可以表示出AG，BG的长度，问题就可以解决.

用三边长表示中线长？我联想到公式“（a＋b）2＋（a-b）2＝2（a2＋b2）”，有思路了！

设BC＝a，AC＝b，AB＝c，如图2，延长AG交BC于点E，则E为BC中点，由得到

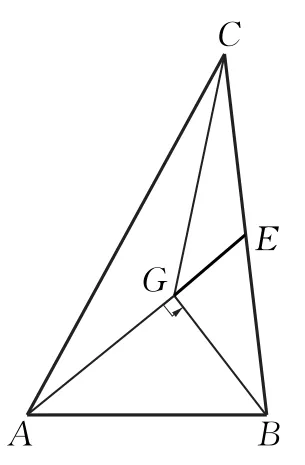
图2

因为AG⊥BG，所以，

整理得，a2＋b2＝5c2，所以cosC＝，

所以C为锐角，.

立即向老师汇报我的做法，老师很赞赏.却又提出一个问题：从形的角度看，还有其他想法吗？

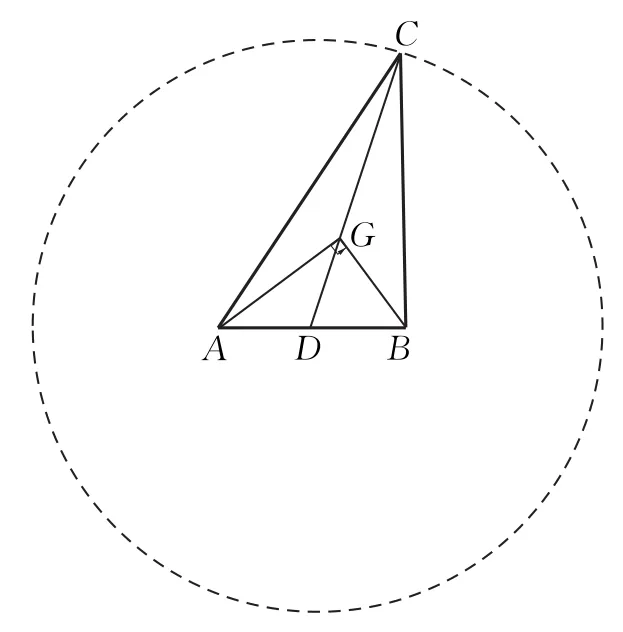
图3

如果从几何的角度去思考：由AG⊥BG，则，所以.若固定A，B两点，则点C的轨迹是圆D（去除直线AB上两点），如图3，则∠ACB显然是锐角.再往后，却无从下手！

突然联想到“张角最大”的一道经典题：

引例如图4，A（0，a），B（0，b），0＜a＜b，点C为x轴正半轴上一动点，若∠ACB最大，则点C的坐标是________.

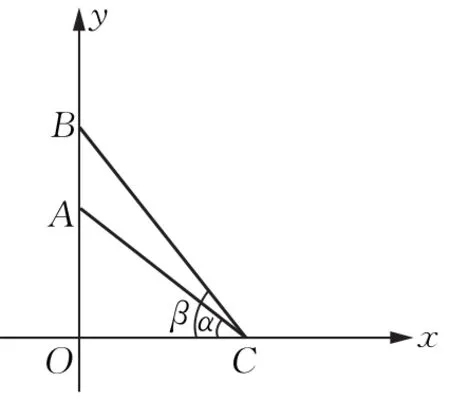
图4

常规做法：构造关于∠ACB的三角函数.

解设C（x，0），x＞0，∠ACO＝α，∠BCO＝β，则∠ACB＝β-α.所以tanα＝，

引例的几何解法：

如图5，过A，B两点作⊙M（当然可以作出无数个圆），若使得⊙M与x轴正半轴相切，则切点即为所求点C（可由平面几何知识证明：∠ACB＞∠ADB）！此时，由切割线定理可以得到：OC2＝OA·OB，即x＝时取“＝”！

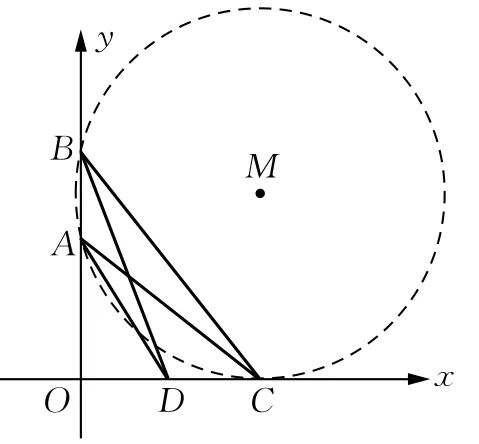
图5

从引例我得到启发：本题不过是把引例中的x轴正半轴换成了⊙D而已，只需找出动⊙M与⊙D的切点即可！

如图6，过A，B两点作⊙M，逐步增加其半径，直至与⊙D内切，显然切点为AB中垂线与⊙D的交点C！此时∠ACB取得最大值.（在⊙D上任选一异于点C的点N，连结AN交⊙D于点K，则∠ACB＝∠AKB＞∠ANB，即可证明）

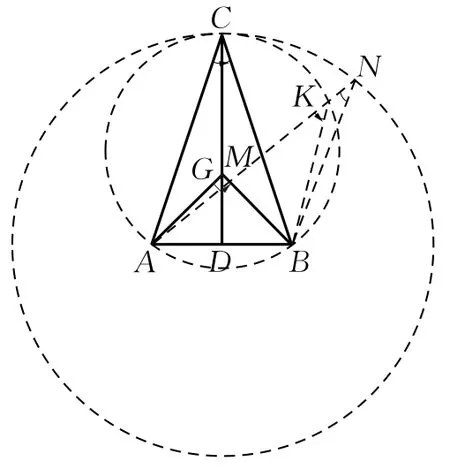
图6

由CA＝CB，，所以sinC＝.

继续思考：刚才的解法中是固定A，B两点.如果固定其他两点呢？比如固定C，B呢？

另解如图7，延长CB至K，使CB＝BK＝2BE，则GB∥AK，故AE⊥AK，则A点在以EK为直径的⊙O上.显然当CA为⊙O的切线时，∠ACB取得最大值.此时，OA⊥AC，易得.

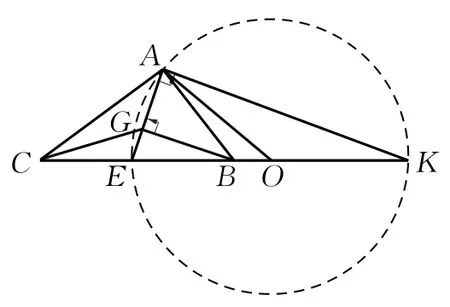
图7

看了我的完整解答，老师笑了：“联想是一种非常有效的解题方式，它不仅能够帮助我们突破思维中的局限瓶颈，拓展思维，还可以提高思维灵活性与想象能力.”

至此，我从几个不同角度探究了本题的一些解法.这些，都是联想得来的.在以后的数学解题中，我们应仔细观察题设条件中的细微之处，发掘题目的隐含条件，大胆联想，从而找到解题的突破口，使得数学问题快速得解.