对一道期末考题的课堂讨论

江苏省姜堰中学 王立振 袁清雯

笔者在讲评一道期末联考题时，做了一些尝试和探索，同学们的课堂表现积极活跃，现整理成文，与大家交流.

1.考题展示

题1在△ABC中，∠BAC＝90°，AB＝2，，EF＝1且EF在BC上移动，则的取值范围为________.

本题主要考查向量的数量积，其主要解决方法有：（1）建立坐标系利用向量坐标运算来求解；（2）线性转化，用向量数量积的定义来求解.

大部分同学遇到的主要困难在于：若用坐标运算求解，如何用一个变量刻画两个动点；若用数量积的定义，与的模和夹角都在变化.

通过下面的课堂交流，同学们和我都是颇有受益.

2.课堂讨论实录

老师：本节课我们来一起交流此题的解决方案，请同学们畅所欲言.

同学1：老师，向量与都在变化，如何求解它们的数量积呢？

同学2：把与转化，假设CE＝x，则有，故有；又由边长之间的关系，可知，进而得到.又因为x∈［0，3］，所以.

老师：同学2解答得非常好！他通过设出一个变量，利用向量之间的相互关系，用一个变量表示多个变量，进而找到一个关于这个变量的函数，将一个向量数量积的取值范围问题转化为关于一个变量的函数值域问题.那么有没有其他不同的想法？

同学3：老师，我知道向量数量积的问题可以建系用坐标来求解：以A为坐标原点，AB所在的直线为x轴建立如图1所示的坐标系.

同学4：建系容易，但是如何用变量来刻画两个动点呢？

同学5：E，F在边BC上运动，且BC上点的横、纵坐标满足关系式.但如何用一个变量来表示两个动点呢？

同学6：如图2所示，过点F作x轴的平行线与过E点作y轴的平行线相交于点D，由EF＝1，易得.

图2

老师：有没有其他同学对上述解法进行补充的？

同学7：题目中“EF在BC上移动”，不仅F的横坐标x∈［0，2］，还要有E的横坐标x-，解得，故的最大值不是15，而是9.

老师：同学们回答得很好，值得表扬.利用建系设坐标的方法来求解向量的数量积，关键在于如何用变量来表示两个动点，同学们注意到了两个动点的横坐标与纵坐标之间的关系以及两点间的距离关系，进而用一个变量来表示，再利用二次函数的性质来求解，但要注意自变量的取值范围.那么，还有没有同学有不同的想法？

同学8：老师，向量的数量积还可以用定义法来解决，但是和的模在变，而且夹角也在变，这怎么求呀？

同学9：我在EF上取中点P，则.因为，所以.

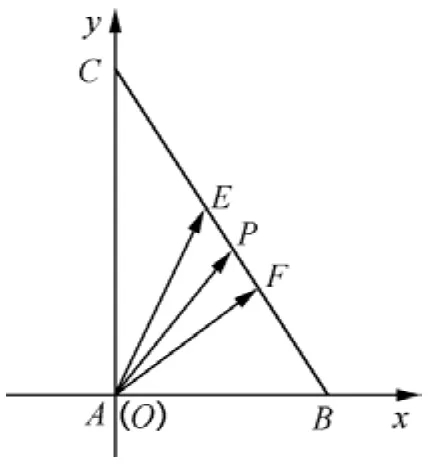
图3

老师：回答得太完美了！将多个动点问题转化为一个动点问题，将陌生的问题转化为熟悉的问题，再运用一些基本方法和基本解题思路，进而解决问题.同学们还有没有其他方法要补充？

同学10：老师，考试的时候，我虽然得到了正确结果，但是我是猜的.

老师：你是怎么猜的？

同学10：因为E，F在线段BC上运动，肯定有一些特殊情况，我就将这些特殊情况都计算一下，然后再比较一下，最后得到的取值范围.

老师：你计算哪些特殊情况下的的值？

同学10：我计算了四种情况：

第一种，如图4①所示，当点E与点C重合时，有，从而得到；

第二种，如图4②所示，当EF的中点与线段BC的中点重合时，有，从而得到；

第三种，如图4③所示，若设EF的中点为点P，则当AP⊥BC时，有，从而得到

第四种，如图4④所示，当点F与点B重合时，有，从而得到，

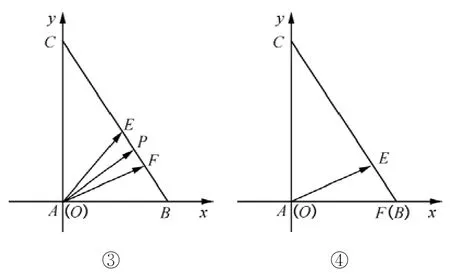
图4

老师：同学们认为这样做可以吗？

同学11：我认为不可以.假如的取值范围不在这几种特殊情况中，而是在一个非特殊点处取得最大值或者最小值，那么同学10的做法就不能得到准确的取值范围了.

老师：虽然这种做法存在一些缺陷，但这种解题思路（特殊与一般的解题思想）是需要引起我们关注的.这种方法不推荐，但需要我们了解，以备不时之需.

3.课后检验

老师：请同学们对这节课的所思所学进行回顾总结，题2、题3作为补充练习.

题2在矩形ABCD中，AB＝4，BC＝3，E，F分别为BC，CD上的任意动点，求的取值范围.

（答案：［0，25］.解决题2的思路是利用特殊与一般的方法，考查的几种特殊情况.）

题3在正△ABC中，AB＝4，EF＝1且EF在BC上移动，求的取值范围.