一道高考函数压轴题的分析与启示

顾肖逸

函数作为高中数学内容的一条主线，贯穿于高中数学学习的始终，并在高考中扮演着重要的角色——它常常以压轴题的形式出现.函数问题凭借其结构形式多变、分类讨论情况复杂等特点，成为高中数学学习中的难点之一.那么面对一道函数压轴题，我们应该如何对其进行分析，从而获解呢？下面以一道高考函数压轴题为例，谈谈我在解决函数压轴题过程中的学习心得，与各位同学分享.

一、试题呈现

已知函数f（x）＝ex＋e-x，其中e是自然对数的底数.

（1）证明：f（x）是R上的偶函数；

（2）若关于x的不等式mf（x）≤e-x＋m-1在（0，＋∞）上恒成立，求实数m的取值范围；

（3）已知正数a满足：存在x0∈［1，＋∞），使得成立.试比较ea-1与ae-1的大小，并证明你的结论.

二、试题的分析与解

1.第一问

第一问比较简单，可直接利用定义解决.首先，函数f（x）的定义域为R，关于原点对称，其次又因为f（-x）＝e-x＋ex＝f（x），所以函数f（x）是R上的偶函数.

2.第二问

第二问的分析与解，我采取了以下步骤进行分析：

（1）认知过程一：这是什么问题？

从题干条件不难看出，这是一个典型的恒成立问题.

（2）认知过程二：我以前有没有处理过类似的问题，如果有，当时是怎么解决的？

可以套用解决恒成立问题的一般方法：参数分离法或构造函数法.

（3）认知过程三：在具体进行操作时，如何选择合适的方法进行研究？

我在学习和研究函数问题的过程当中，积累了如下的解题经验：

①一般来说，如果容易分离的就进行参数分离；

②在参数分离之前，可考虑用换元法将问题进行简化.

由以上的认知过程的分析，我尝试给出了以下解法：

解法1mf（x）≤e-x＋m-1⇔m（ex＋e-x）≤e-x＋m-1，在x∈（0，＋∞）上恒成立，即m（ex＋e-x-1）≤e-x-1；令t＝ex（t＞1）；因为1，当且仅当t＝1时，等号成立；

当t＞2时，h′（t）＞0；则当1＜t＜2时，h′（t）＜0；因此可知当t＝2时，h（t）有极小值.

（注：解法1在参数分离后利用导数方法求得函数的最小值.）

解法2由题意知，m（ex＋e-x）≤e-x＋m-1在（0，＋∞）上恒成立，令t＝ex，则t＞1.所以对任意的t＞1恒成立，注意到2＋1＝3，当且仅当t＝2时等号成立，所以，故，因此m的取值范围为.

（注：解法2在参数分离后利用基本不等式方法求得函数的最小值.）

（4）认知过程四：本题如果利用构造函数的方法进行研究，如何对参数进行分类讨论呢？

通过构造函数解决恒成立问题，分类讨论是无法避免的，那么如何有效进行参数的分类讨论呢？我的体会和经验是如果要分类讨论，一定是产生解题冲突的结果.

比如对于含参的二次函数f（x）＝ax2-2x＋1来说，此时产生的认知冲突是它到底是什么函数？可能是一次函数，也可能是二次函数（开口可向上也可向下），因此需分为a＞0，a＝0，a＜0三种情况讨论；再比如函数f（x）＝x2-（a＋1）x＋a，它可以因式分解为f（x）＝（x-1）（x-a），此时产生的认知冲突是其零点的大小，因为需分为a＜1，a＝1，a＞1三种情况讨论.以下利用构造函数的方法不难给出本题的解法：

解法3由条件知m（ex＋e-x-1）≤e-x-1在（0，＋∞）上恒成立，令t＝ex（t＞1），则有，对任意的t＞1恒成立.令，

（注：因为分母恒正，分子的正负决定了g′（t）的正负，从而影响函数的单调性，分子部分即是前面所分析的含参的二次型函数，因此先对m＝0，m＞0，m＜0三种情况讨论.

（1）当m＝0时，，g（t）在（1，＋∞）上单调递增，所以g（t）＞g（1）＝m＝0，所以m＝0舍去；

（2）当m＞0时，y＝mt2-m＋1在（1，＋∞）上单调递增，mt2-m＋1＞1＞0，g（t）在（1，＋∞）上单调递增，所以g（t）＞g（1）＝m＞0，所以m＞0舍去；

（3）当m＜0时，由，易知g（t）在上单调递增，在上单调递减，所以，解得.

3.第三问

第三问的分析与解，可以类比第二问的步骤进行分析：

（1）认知过程一：这是什么问题？

从题干条件不难看出，本题可分解为两个小问题：

问题1：∃x0∈［1，＋∞），使得成立，求参数a的取值范围.

问题2：利用问题1得到的参数a的取值范围，比较ea-1与ae-1的大小.

问题1是一个典型的不等式有解问题，问题2则是一个比较代数式的大小问题.事实上，很多函数压轴题都可以进行这样的难题分解.将难题进行分解，然后逐一解决，有时即使解决不了最终的问题，但能解决分解后的几个小问题，从考试来说，也能得到可观的分数.

（2）认知过程二：我以前有没有处理过类似的问题，如果有，当时是怎么解决的？

不等式有解问题方法和恒成立问题一致，仍然可考虑参数分离法或构造函数法.

对于比较大小问题，可考虑构造函数的方法解决.

由以上的认知过程的分析，我尝试给出了以下解法：

难题分解1：∃x0∈［1，＋∞），使得成立，求参数a的取值范围.

分解路径1（构造函数法）：

令g（x）＝f（x）-a（-x3＋3x），只要在x∈［1，＋∞）上，g（x）min＜0即可.

分解路径2（参数分离法）：

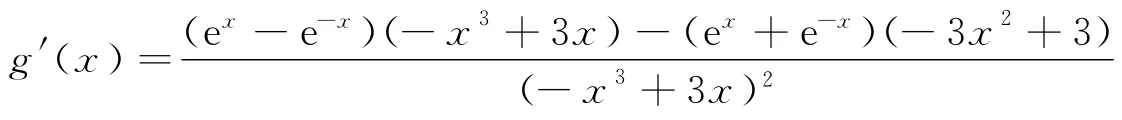
（注：可能会有同学一阵眩晕，别怕，先从函数解析式的角度进行观察，在定义域上，分子部分是单调递增的函数，分母部分是单调递减的函数，且分子和分母均大于0恒成立，g（x）还不是单调递增吗？有了这个目标.对接下去的证明工作起了很好的导向作用，通过观察，我们猜想g（x）是一个单调递增的函数，那还不应该大于0恒成立吗？）

难题分解2：如何根据求得的参数a的取值范围比较ea-1与ae-1的大小？

分解路径1（取对数后构造函数比大小）：

由于ea-1与ae-1均为正数，同取自然底数的对数，即比较（a-1）lne与（e-1）lna的大小，即比较与的大小.

（注：取对数思想在高考题中的体现可追溯到1992年全国高考题：

（1）已知a，b为实数，且e＜a＜b，其中e是自然对数的底数，证明ab＞ba；

（2）如果正实数a，b满足ab＝ba，且a＜1，证明：a＝b.）

分解路径2（变同底，构造函数比大小）：

要比较ea-1与ae-1的大小，由于ae-1＝e（e-1）lna，那么，故只要比较a-1与（e-1）lna的大小.

令h（x）＝（e-1）lnx-（x-1），那么，当x＞e-1时，h′（x）＜0；当0＜x＜e-1时，h′（x）＞0；所以在区间（0，e-1）上，h（x）为增函数；在区间（e-1，＋∞）上，h（x）为减函数.

又h（e）＝0，h（1）＝0，则；那么当时，h（a）＞0，eh（a）＞1，ae-1＞ea-1；当a≥e时，h（a）≤0，0＜eh（a）≤1，ae-1≤ea-1.

三、试题解决的启发

通过以上的分析，我们不难总结出一些解决函数压轴题的思路，也同时能获得一些良好的解决函数问题的活动经验.

首先，我们对问题进行总体感知，确定问题模型，即明确该问题涉及的基本问题是什么，以及主要的解决方案是什么，从而形成良好的解题结构.以本题为例，本题涉及了高中函数的重要问题：恒成立问题和存在性问题.由此，我们利用解题学习获得的经验明确这类问题的解题方向：对函数的最值加以研究，并对命题进行转化.而对于这两类问题，常见的研究方法是参数分离法和构造函数法.

其次，对条件的结构加以观察，选取解决问题的最优方法.以本题为例，在第二问的解决过程中不等式的结构形式较为清晰，容易进行参数分离，参数分离是本题的最优方案，避免了冗杂的分类讨论，但在第三问中，结构形式较为复杂，我们倾向于选择直接构造函数的方法，事实也证明了我们的分析——第三问如果进行参数分离，最后得到的结构比较复杂，容易造成恐慌.因此，在解决问题之前，选择合适的解题策略也应包含在问题解决的过程之中.

最后，对难题进行分解.综合题之所以成为综合题，可能是由多个知识点组合而成的，或是由多个基本题拼凑形成的.对于一些较难的函数问题，当实在啃不动时，一个明智的做法是：可以将它划分为几个子问题或一系列的步骤，尝试去解决问题的一部分，得到相应的得分，从而尽可能提高压轴题的得分.