是概率出问题了吗

赵秋雨

我曾遇到过这样一题：

在半径为1的圆内任作一条弦，则弦的长度超过该圆的内接等边三角形边长的概率是多少？

这显然是一个几何概率问题.我的解法是这样的：

分析与解

法一如图1，△ABC为圆O的内接等边三角形.现在圆内任意作弦.由于对称性，不妨将弦的一端固定在△ABC的顶点A处，当弦的另一端点P落在劣弧上时，PA＞AB.当点P落在以外的圆周上时 ，PA＜AB.（不考虑弧的端点处）

假设事件E表示“任意所作的弦的长度超过圆内接等边三角形的边长”，ω表示事件总体，这时，于是

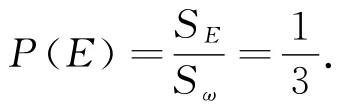
或者类似地，

法二如图2，不妨将弦的一端固定在等边三角形的顶点A处，另一端绕着圆O运动，即令弦AP绕着点A旋转.

若l为圆O在点A处的切线，则与此切线交角在和之间的弦才能超过△ABC的边长.而所有弦与切线l的夹角在0到π之间，故

然而，本题的参考答案却给出了完全不同的解法和结果：

法三如图3，圆内弦的位置被弦的中点唯一确定.在圆内作一同心圆，其半径为大圆的一半.则当弦的中点落在小圆内时，弦长才能大于圆内接正三角形的边长.

图1

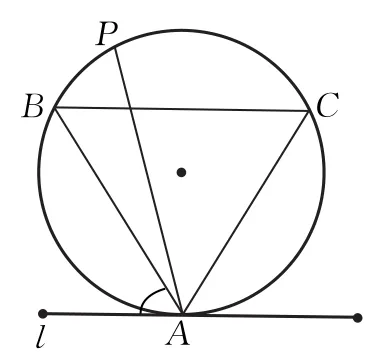
图2

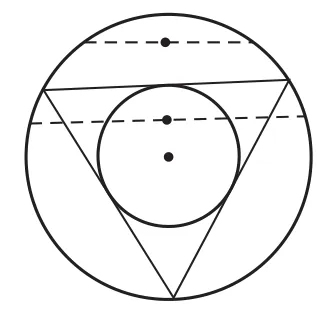
图3

并且参考答案中说，这是一个贝特朗问题，答案并不唯一.

这令我疑惑不解！老师告诉我们，概率是随机事件本身固有的属性，不会随着试验次数、计算方法等因素而有所改变.在这个问题中，同一事件的概率，为何会因为计算的角度不同而得到不同的答案呢？难道是概率本身出了问题？

通过认真思考和查阅资料，我终于发现不是概率出了问题，而是“人”出了问题.数学是一门严谨的学科，问题的求解方法可以有多种，但结果应该一致.贝特朗问题之所以会出现不同的答案，是因为人们观察随机试验的基本结果的角度不同，同时对结果的等可能性假设也有不同的理解.

例如我的解法1中，当弦的一端A固定后，我所认为的等可能结果是：弦的另一端点P在圆弧上是等可能出现的.问题转化为点P落在圆周的某段弧上的概率问题.结合解法3，如果也以弧的中点来考虑问题：当点P从点A出发沿圆周运动一周时，弦PA的中点M的运动轨迹是一个以OA的中点为圆心，半径为的圆（如图4，此处证明略）.当点P落入劣弧内时，对应的中点M的轨迹为.而的度数为，所以所求的事件概率为

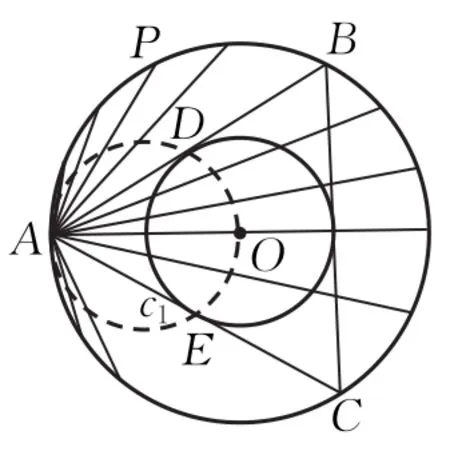
图4

也就是说，同样以弦的中点来考虑问题，当假定弦的一端固定时，本题中随机事件对应的几何量为一维的曲线长度；而若不固定弦的端点，在区域内随机作弦时，事件所对应的几何量则为二维的图形面积.并且所得的结果不同.看来并不是概率出了问题，而是我们思考问题的角度发生了变化，是我们的“假设”出了问题.