仅知失效数的指数型元件失效率的估计

陈玉阳，吴和成，胡明月

（1.大连理工大学 石油与化学工程学院，辽宁 盘锦 124221；2.南京航空航天大学，a.经济与管理学院，b.理学院，南京 211106）

指数型产品的失效率评估问题，在可靠性理论和应用中比较常见，而且一直受到关注，但不同试验类型的数据对于元件失效率或元件的可靠性评估带来的困难各异。对于定数截尾或定时截尾试验数据，可以得到指数型元件失效率的显式估计[1]。对于贮存设备，因其不处于运行中，往往得不到其准确的失效时间，只能通过定期检测来确定设备是否失效，而失效设备的确切寿命是未知的。

对于不确定数据的可靠性估计研究，Dempster等[2]于1977年提出，在不完全数据情况下，利用EM算法来解决可靠性估计的问题。木拉提等[3]对删失数据的对数正态分布参数估计和混合正态分布参数的最大似然估计进行了模拟，模拟结果表明，EM算法是有效的，估值精度满足要求。Tan[4]将EM算法应用于串并联系统中，有效地解决了基于不确定数据的系统可靠性估计问题。1976年 Turnbull[5]提出了求删失数据的广义最大似然估计的 SC（self-consistant）算法，随后GU等[6]建立了SC算法估计的一致性和正态性，近年来SC算法仍然广泛应用于可靠性评估中。徐永红等[7]提出基于均值插补法和最近邻插补法的非参数估计方法，相比于经典 SC算法，该算法具有更高的精确度和更好的稳健性。平均秩次法[8]是一种在随机截尾条件下经验分布函数的计算方法。沈安慰[9]在可靠性数据分析中引入累积法，结合平均秩次法解决随机删失数据下的参数估计问题。Olgierd[10]认为，在实际应用中，获取的数据往往是不确定的，并提出用模糊 Bayes方法对可靠性评估进行研究。Peng等[11]基于包含区间删失数据的可修系统，提出蒙特卡洛期望最大化算法（MCEM），可以有效地对系统的可靠性进行评估和预测，并通过仿真和实例证明了方法的有效性。A.Regattieri等[12]通过轻型商用车制造系统案例研究，说明了故障过程建模（FPM）方法对于不确定数据的可靠性估计是有效的。David等[13]基于模糊概率理论，对仅含有删失数据的元件可靠性进行了估计。B. García-Mora等[14]认为，在可靠性试验中，不能准确地观测到产品的失效时间，他们利用广义非线性模型对产品的失效率进行估计，并可以预测未来某一时刻产品的可靠度。Zhao等[15]应用三角模糊数的方法对航空发动机的可靠性进行了预测。Ogryczak W[16]针对选址问题，综合考虑空间的利用率，应用条件中位数方法求解了k-centrum模型中的参数。范大茵[17]应用条件中位数的方法来估计元件的失效率，并讨论了可靠性置信下限的问题。胡斌等[18]认为，条件中位数方法对尚未发生的事件进行了外推，并在其基础上加以改进。

对于不确定数据的可靠性估计，国内外文献通常基于 EM 方法，用条件期望代替寿命的估计，但是EM方法必须通过牛顿迭代法计算，不仅计算繁琐，还必须考虑迭代是否收敛的问题。最大似然估计法计算简便，估计量具有一致性和有效性，但有时难以得到估计量的解析式。模糊理论方法可以综合考虑不确定信息，但是信息简单的模糊处理将导致估值精度降低。条件中位数方法计算简便，且必存在收敛于方程的根。文中基于文献[17]和[18]提出的基于条件中位数的改进方法，针对仅知失效元件数的试验数据，对指数型元件的失效率进行估计。

1 试验数据

设元件的寿命x服从参数为λ的指数分布，其分布密度为：

式中：λ未知，且λ∈ R+。在t0=0时刻以n个元件进行寿命试验，记 0= t0＜ t1＜ t2＜… ＜ tk，在时刻ti观测时间区间[ti-1,ti）内失效的元件数，结果见表1。此类数据的特点是：仅知在某时间段内失效的元件数，而不知失效元件的确切寿命。

表1 试验数据

2 元件失效率的估计

如要估计元件在 t时刻的可靠度 R(t)=e-λt，则先要估计元件分布中的参数λ。在完全样本情形，即有全部被试验元件的寿命数据 x1, x2,… ,xn，则λ的最大似然估计值为：

对于表1数据，容易得到参数的似然函数：

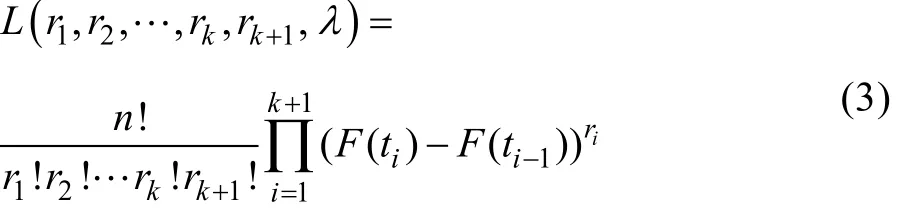
若对观测区间没有限制，则由式（4）难以得到参数λ最大似然估计的显式表达式。如对于观测区间为等间距情形，可以获得λ最大似然估计的显式表达式。 不妨 记， 对一 切 i = 1,2,… ,k 。 再记，则：

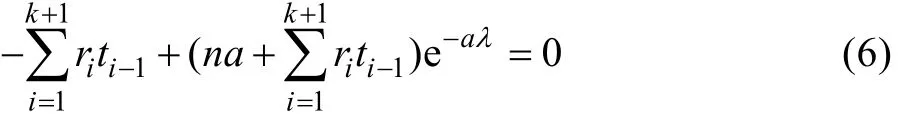
从而：

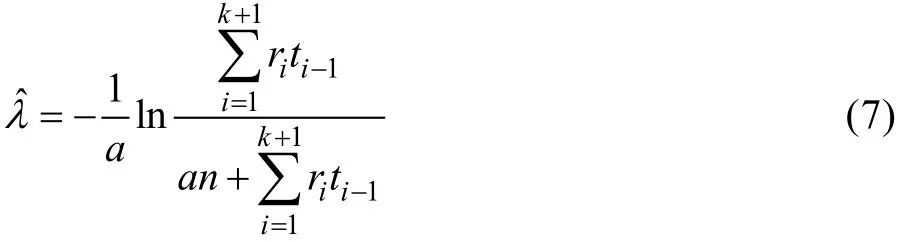
对于观测时间间隔不等情形，无法得到元件失效率最大似然估计的解析式。因此，对于一般情形下，一个自然的想法是否可以用区间[ti-1,ti）中的一个数作为元件寿命的估计值。由此，再利用式（2）得到元件失效率λ的一个估计值。由于元件寿命服从指数分布，因此，如用区间中点作为元件寿命的估计值不合理。一个有统计意义的数值，即利用条件中位数作为元件寿命的估计值具有直观合理性。

3 失效率估计的改进方法

以满足下列方程的 μi作为寿命在[ti-1,ti）中的元件寿命的估计[17]：

即有：

从而有：

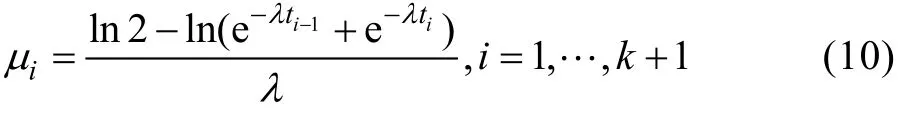
将[ti-1,ti）内失效的 ri个失效的元件的寿命均近似看作 μi，则由式（2）可以得到 λ的近似估计值为下列方程的根：

整理得：

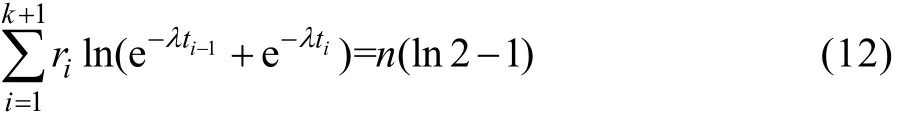
如记：

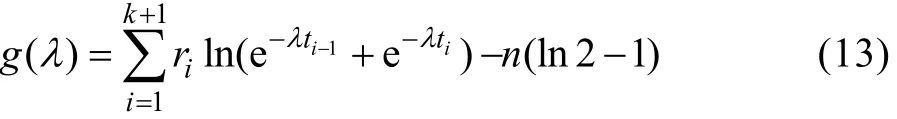
即g(λ)是λ的严格单调递减函数。另外，容易验证 g (0) ＞ 0,g(+ ∞ ) ＜ 0，故g(λ)=0有唯一正解。

文献[18]对此方法加以改进，认为条件中位数方法对尚未发生的事件进行了外推，其给出的估计为：

将μi代入，并整理，得：

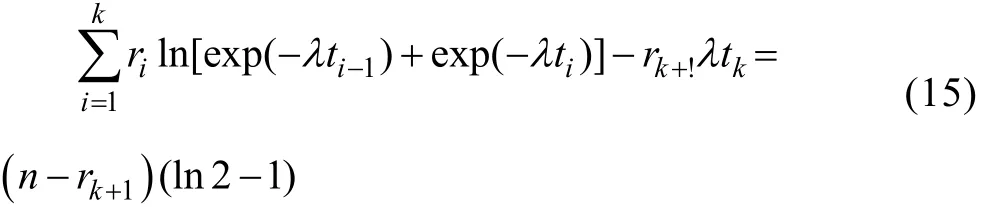
相比于文献[17]，文献[18]效果更好，但缺乏统计含义。为兼顾效果和含义，提出一种基于条件中位数的改进方法，即用代替μk+1作为未失效元件的寿命估计。

将μi代入，并整理，得：

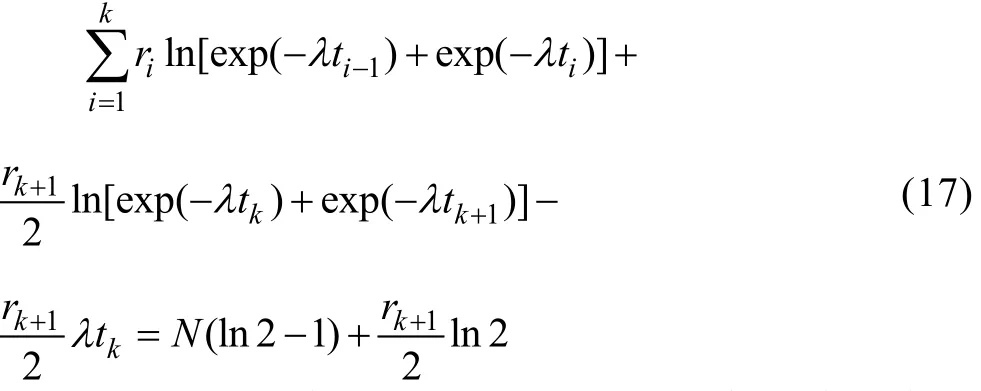
从上述方程求出λ，即得元件失效率的估计值。显然，式（17）的求解需要数值解法。

4 估计的优良性

为比较三种方法的估计效果，采用文献[18]的方法进行仿真。

4.1 仿真原理

假设n个元件在t0=0时刻开始贮存，在规定时刻ti( i = 1,2,...,k )进行定检，并且其贮存失效率 λ已知。按 指 数 分 布 随 机 生 成 失 效 时 刻 ξj( j = 1,2,...n)， 若ti-1＜ ξj≤ ti，认为元件在定检区间 （ti-1,ti]内发生一次失效，由此得到产品在定检区间内的失效数ri( i = 1,2,...k )和 rk+1。把 n，ti( i = 1,2,...,k )，ri( i = 1,2,...k)和 rk+1分别代入式（12）、（15）、（17），迭代求解出 λ的对应估计值ˆ 。重复该过程m次，得到m个，分析诸的统计特性并与真值 λ比较，对文献[17]、文献[18]和文中方法的估计效果进行分析。

4.2 仿真步骤

1）给常量 λ，n，m和 ti( i = 1,2,...,k )赋值，令失效数 ri( i = 1,2,...,k)和rk+1的初值为0。

2）生成失效时刻 ξj( j = 1,2,...n)：利用随机数生成命令产生（0, 1）指数分布的伪随机数ηj，按式（18）计算jξ：

ξj就是贮存失效率为λ时元件的随机失效时刻。

3）求定检区间失效数 ri( i =1,2,...k)和rk+1：将ξj与定检时刻ti进行比较，ξj必落入某一个定检区间。若 ti-1＜ ξj≤ ti， 则 ri=ri+1； 若 ξj＞ tk， 则rk+1= rk+1+ 1。取 j= 1,2,...n，重复n次后，得到求解模型方程所需的 ri( i = 1,2,...k )和 rk+1。

4） 求 解 仿 真 方 程 ： 将n， ti( i = 1,2,...,k)，ri( i = 1,2,...k )和 rk+1代入式（12）、（15）、（17），分别得到三种方法的仿真过程。迭代求解非线性方程，求出真值λ的对应估计值

6）计算三种方法的估计均值、估计标准差和相对估计误差。

4.3 仿真结果

数字仿真用 Matlab语言实现。取 m=1000。取t1=0.5，t2=1.5，t3=2，t4=3，t5=4.5，t6=5，t7=6.5，t8=7.5，t9=9，t10=11（单位：a），真值λ分别等于0.1，0.25，0.4，0.5，0.8，1，1.2（单位：1/a）。分别对 n=50，n=100，n=200进行仿真，仿真的结果见表2。

由表2可以看出：当真值λ取0.1，0.25， 0.8，1，1.2时，应用文献[17]的方法得到的估计值的相对误差较大。当λ=0.1，n=50时，相对误差达到64.16%，而文献[18]和文中方法得到的估计值的相对误差较小。当真值λ取0.4和0.5时，三种方法得到的估计值的相对误差都较小。当λ=0.5，n=50时，三种方法得到的估计值的相对误差分别为 3.39%，3.37%和2.87%，文中方法得到的估计值更贴近真值。当真值λ=0.4，n分别为50、100、200时，文中方法得到的估计值的相对误差分别为 1.13%，0.89%和 0.67%。即随着样本量的增加，应用文中方法得到的估计值的相对误差越来越小。

表2 仿真结果

续表2

表3 某指数型元件试验数据

因此，文中提出的方法相比于文献[17]和文献[18]的方法，估计值的均值更接近真值，相对误差较小，估计结果得到改善。

4.4 实例分析

某指数型元件试验数据见表3，其中n=20，k=6，代入式（17），应用Matlab计算得到λ=0.3687。则元件的可靠度为 R( t) =e-0.3678t

5 结语

针对文中试验数据的特点，提出了一种失效率的估计方法。对于仅知在某时间段内失效的元件数，而不知失效元件的确切寿命这类数据，提出估计失效率的改进的条件中位数方法，进而可以估计元件的可靠度。仿真结果表明，文中提出的方法估计结果得到改善，可以应用于实际中。