基于蒙特卡洛法的曲轴结构优化分析

朱宜生 ，刘玉石

（1.中国船舶重工集团第七二三研究所，江苏 扬州 225001；2.中国船舶工业电工电子设备环境与可靠性试验检测中心，江苏 扬州 225001）

随着全球化进程的加快，大型动力机械的需求也随之增加，曲轴作为柴油机的主要组成部分，其可靠性和经济性十分重要。曲轴的主要破坏方式是圆角处产生裂纹甚至断裂，这会导致柴油机失去动力，造成不可预知的后果。因此，有必要对曲轴的强度进行分析，以防止疲劳破坏，这对确保柴油机的性能和可靠性，指导进一步的结构优化具有重要意义。

有限元方法是一种经典的数值求解方法，可用于解决柴油机曲轴的各种振动问题。国内外科研人员对曲轴进行了大量的有限元振动响应分析，并取得了一系列的研究成果。斯塔尔 G.以单曲柄为研究对象，通过测量单曲柄的主要参数对圆角的影响来得到影响曲线[1]。Cyrus Kano对许多曲轴的弯曲疲劳强度进行了测试，通过对该数据的分析，总结出单个几何参数与曲轴强度之间的关系[2]。Health和 Namara结合有限元方法和经典分析技术对曲轴应力进行分析，为曲轴的优化设计提供参考[3]。Nallicheri等人基于制造经济学对汽车曲轴的材料选择进行了广泛研究[4]。W Y Chien用二维有限元网格计算得到单曲柄的应力强度因子[5]。Gupta对曲轴进行了不同材质下的动态仿真，并从几何和材料上对曲轴进行了优化[6]。

文中建立了一种V型16缸柴油机曲轴的单曲柄模型，并利用ANSYS进行静态分析计算。根据发动机实际工作过程，设置载荷和边界条件。为了简化计算过程，建立了曲柄中心竖向界面的二维网格模型，通过ANSYS的PDS模块对单曲柄进行优化，主要变量为主轴直径、曲柄销直径和圆角半径。

1 理论模型

在柴油机的工作过程中，曲柄连杆机构的受力主要包括气缸内的气体压力、往复运动质量的惯性力和曲轴上的其它载荷。在本文的分析中，扭矩对应力的影响较小，因此只考虑在最大爆发压力作用下的曲柄销上的弯矩。文中所述的16V170型柴油机参数见表1。

表1 柴油机主要参数

作用在活塞上的气体压力如下：

在柴油机膨胀冲程中，制造商给出最大爆发压力为14 MPa，发生360°曲柄转角时，然后用式（1）计算曲轴的气体压力.

在计算曲柄连杆机构的惯性力时，由于连杆大端和连杆小端的运动形式不同，连杆质量一般分为两部分。一般来说，质量分布如下：结合式（2）和（3），往复直线运动质量和旋转运动质量如下：

通过以上的分析，往复直线运动质量和旋转运动质量的惯性力如下：

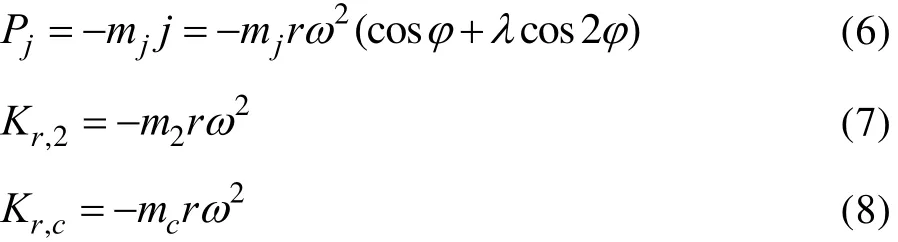
图1显示出Pg和Pj作用在同一条直线上，合力如下：

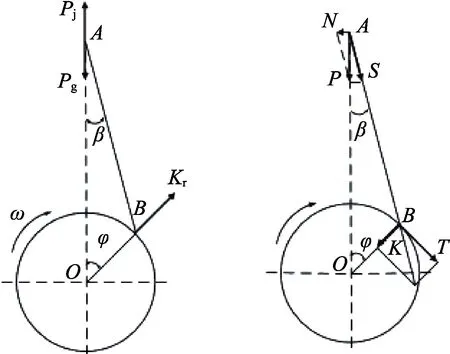
图1 曲柄连杆机构的作用力

图2显示各分力K，N，S，T的关系，通过以下公式计算得出：

作用在曲柄销上的合力为：

图2 单柄曲拐模型

将表1的数据带入式（15）计算得出，Pc=303222 N。

2 有限元分析

2.1 单个曲柄有限元分析

文中采用三维建模软件 Pro/E建立单位曲柄简化模型，如图 2所示。单曲柄包括 2个主轴颈，2个曲柄臂和1个曲柄销。表2列出了单位曲柄的几何和材料属性，其中 σDWH和 σDWG根据参考文献[7]计算得出。

将几何模型导入Hypermesh进行网格划分，将模型单位修改为mm，单元类型定义为Solid185。然后，将网格模型导入ANSYS，根据实际工作环境加载边界条件。约束左右两个端面在x轴和y轴方向的位移以及主轴颈的径向位移。图 3是划分后的网格模型，根据油膜压力分布的约束和载荷模型设置如图4所示。

约束边界条件和加载后，下一步进行求解。

观察图5和图6所示的应力云图和位移云图，发现曲轴中垂面的应力和位移最大。最大位移0.22 mm，最大应力发生在主轴颈附近的圆角上，为104.7 MPa，小于所允许的主轴颈圆角处的疲劳强度（σDWG）。该模型存在较大的应力剩余，并留有空间进行轻量化优化设计。

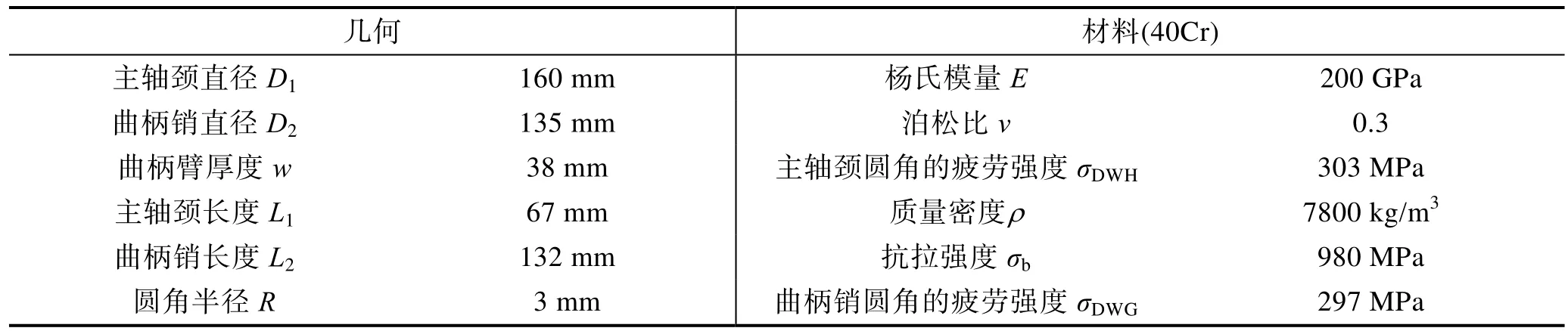
表2 单柄曲拐的几何和材料属性

图3 有限元模型

图4 约束及加载

2.2 2D有限元分析

为了优化曲轴，必须对曲柄进行参数化。三维模型的参数化比较复杂，因此，根据参考文献[5]，首次进行了弹性二维平面有限元模型分析，以了解曲轴弯曲时应力集中的性质，其几何为单曲柄的中间垂直面，单元类型为Shell181。等效负载和约束与2.1节相同，如图7所示。

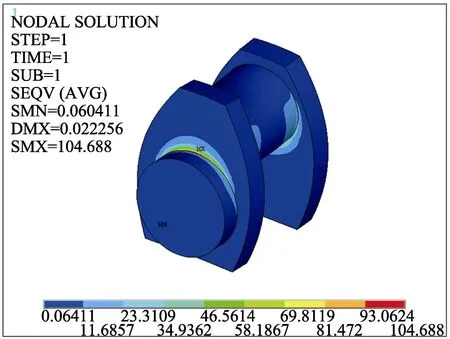
图5 应力云图

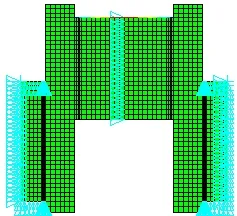
图7 二维模型的约束和加载

将二维网格模型导入到ANSYS中，计算结果如图8、图9所示，最大的Von Mises应力为103.8 MPa，最大位移为 0.33mm，与三维模型比较误差很小，且最大应力发生的位置与三维模型相同，即二维有限元模型是可靠的，可用于曲轴的优化设计。

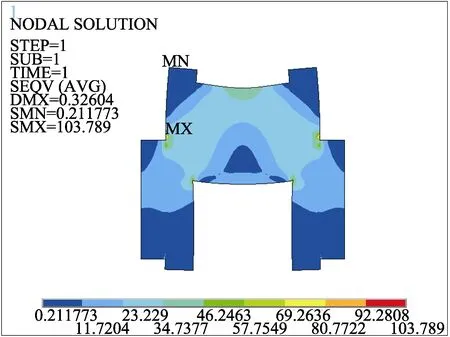
图8 应力云图

图9 位移云图

3 几何优化过程

在笔者的研究中，减少质量同时改善或维持原曲轴的应力性能是主要目标。对应力云图的研究表明，主轴颈、曲柄销等部位应力较低，可以改变其直径以减小其质量。此外，为了避免由于D1和D2的变化而增加圆角区域的应力，必须增加圆角半径R，以维持应力水平。

3.1 D1和D2的作用

在这一节中，应用ANSYS PDS模块对单曲柄结构进行优化[8]，这是一种基于现有有限元分析结果的抽样分析方法。首先，用 ANSYS的参数化语言(APDL)编写分析文件，然后定义D1和D2的数值变化范围，见表 3。由于连杆大端的间隙为 13 mm，D1和 D2的变化不会影响柴油机的整体结构。最后，基于蒙特卡洛法中拉丁超立方（LHS）的抽样方法[9]，对有限元模型进行500次抽样分析。

从图10和图11可以清楚地看到，最大应力的范围是80~120 MPa，远远低于σDWG；最大位移的范围是0.044 ~0.057 mm，结果合理。对比图12a与图12b，发现 D1和 D2对最大应力的线性相关系数为-0.9033和0.4221。换言之，最大应力随 D1的增加而减小，随D2的增加而增大，D1对最大应力的影响大于D2。经过分析可以得到最优化的尺寸：D1=150 mm，D2=125 mm，优化后模型的最大应力是107 MPa，略高于未优化的结果。

表3 D1和D2的变化范围 mm

图10 最大应力范围

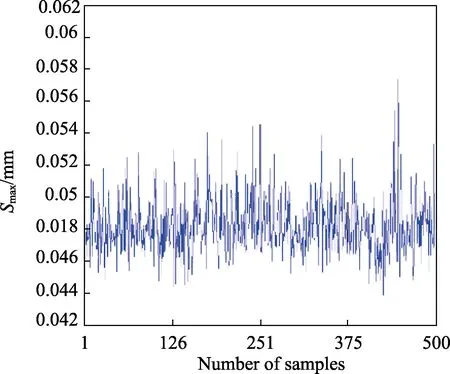
图11 最大位移范围

3.2 R的作用

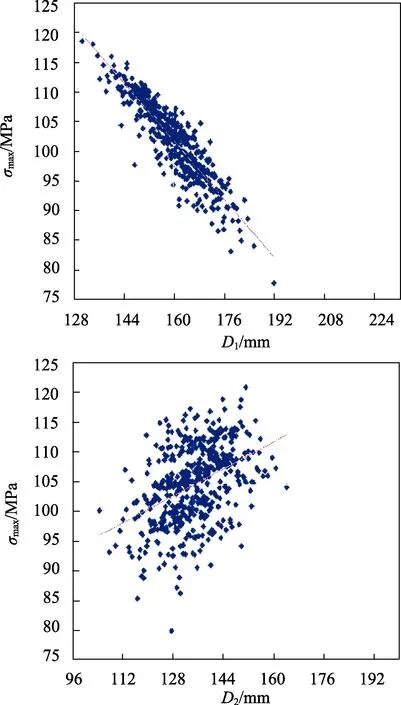
图12 D1和D2对最大应力的影响

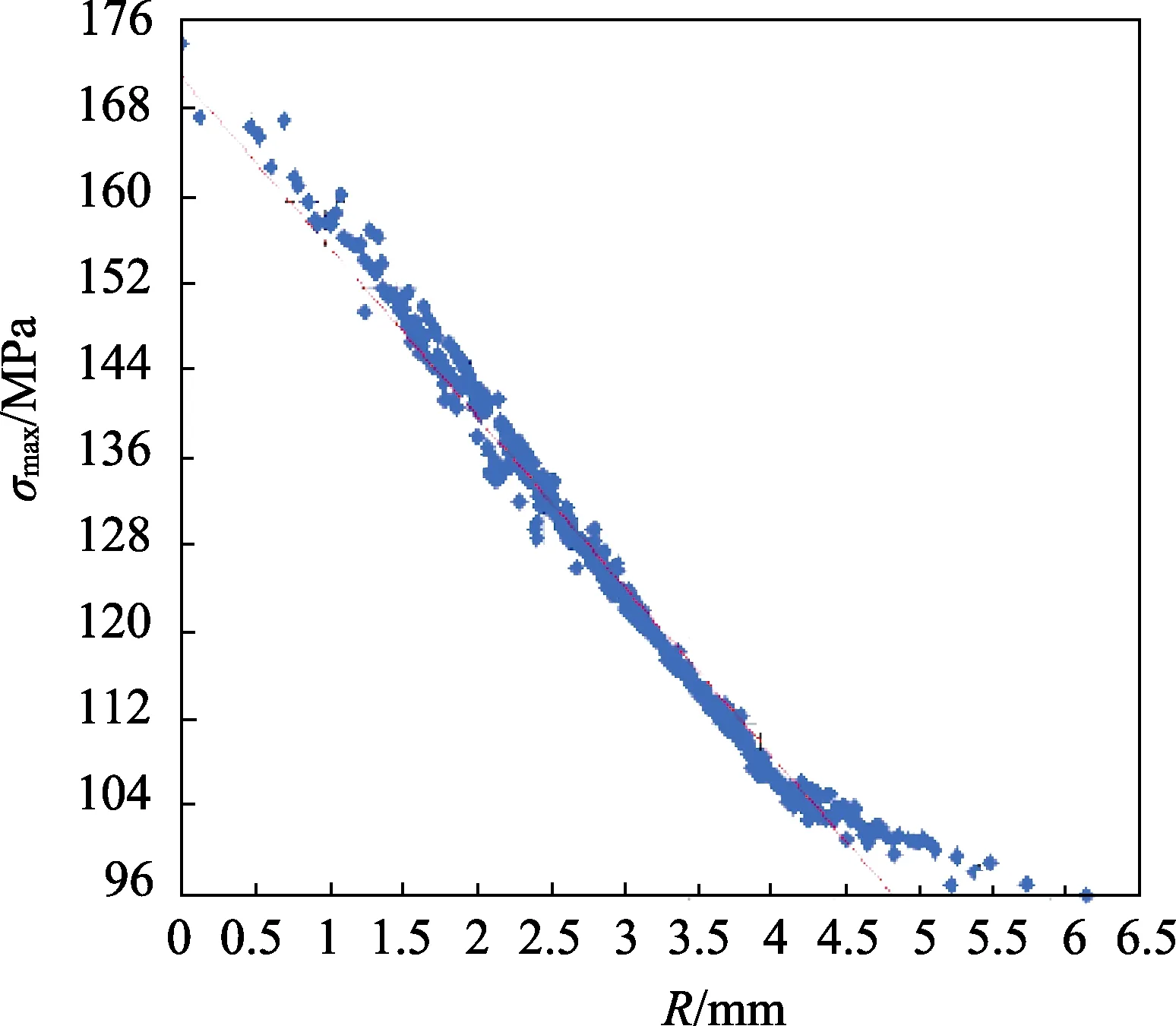
图13 R对最大应力的影响

在本节中，再次使用 PDS模块探讨在优化尺寸下R对于曲柄最大应力的影响。如图13所示，R的数值范围为 0.1~6.5 mm，最大应力范围为 96.3~174 MPa。R在0.1~4.5 mm之间时，最大应力随圆角半径的减小下降迅速；R在 4.5~6.5 mm之间时，最大应力随圆角半径的减小下降缓慢，R=4.5 mm的位置是转折点，该点的最大应力在许用范围内，因此，R的优化尺寸为4.5 mm。

为了保证优化结果的可靠性，应检验优化结果。由Pro/E创建三维模型，参数设置如下：D1=150 mm、D2=125 mm、R=4.5 mm，划分网格和分析模型参考2.1节，优化后的结果如图14、15所示。优化的单位曲柄最大应力为 76.0 MPa，比优化前减少了 28.7 MPa，小于 σDWH，满足强度要求。最大位移为0.0289 mm，比优化前曲柄增加了0.007 mm，小于最大允许位移值0.05 mm，满足刚度要求。在几何优化过程中，单曲柄质量降低了 3.37 kg，整个曲轴质量降低了26.99 kg，在减少最大应力的情况下达到降低曲轴质量的目的。

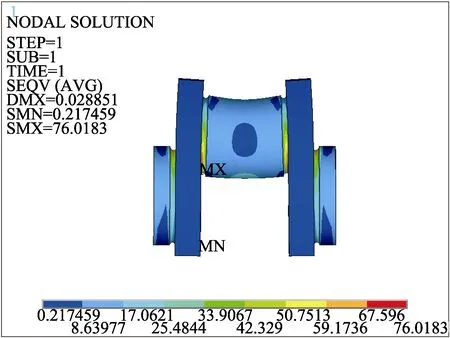
图14 优化后的曲柄的应力云图

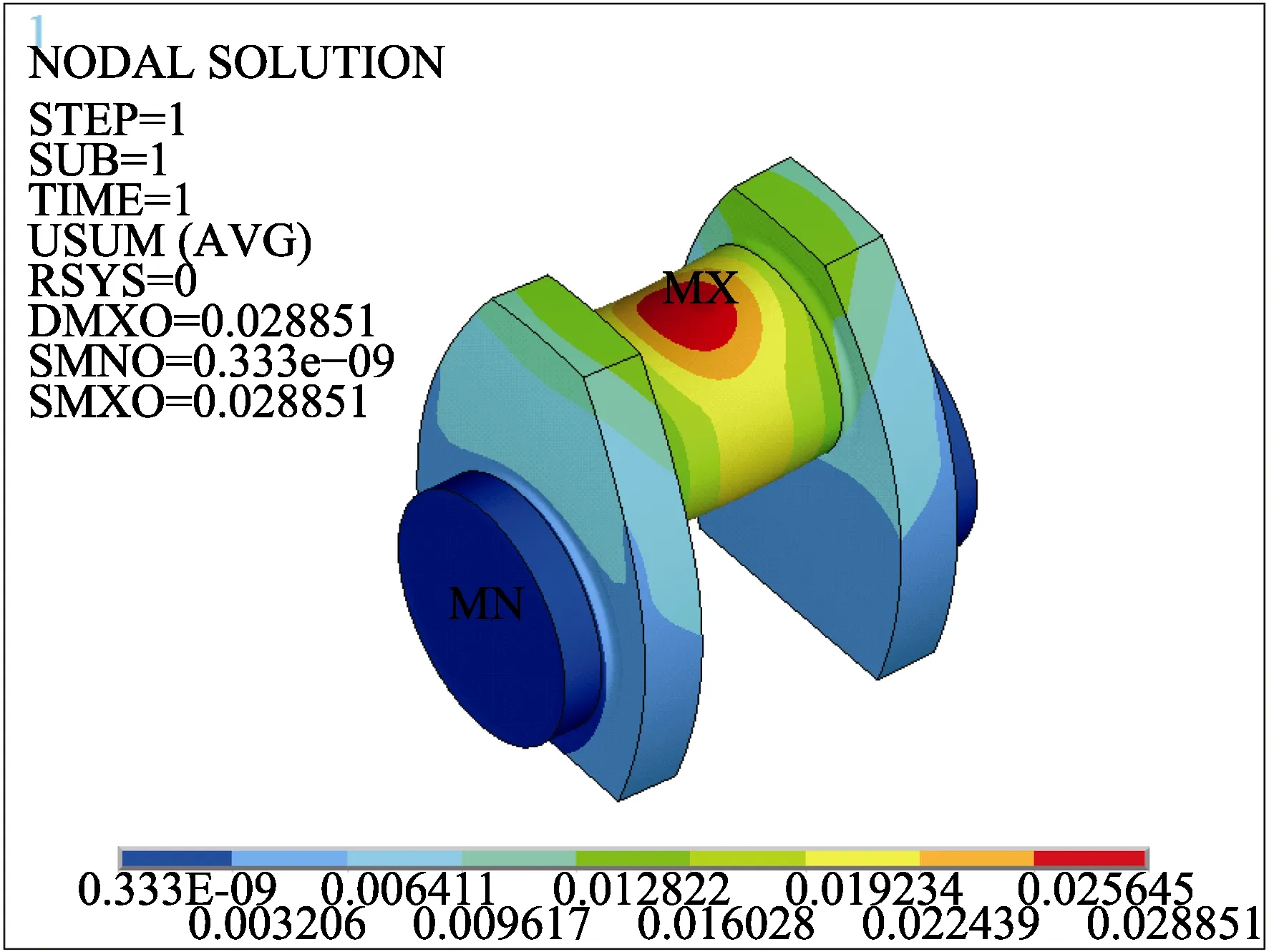
图15 优化后的曲柄的位移云图

4 结论

首先应用ANSYS建立并计算了单曲柄的三维有限元模型，得到了在实际加载条件下的最大应力和位移。此外，为简化计算，建立了弹性二维平面有限元模型，验证了二维模型的合理性，可代替三维模型进行计算。最后，讨论了各种几何参数(D1、D2和R)下的最大应力，分析了这些参数对最大应力的影响。结果发现，D1与最大应力是正相关，D2与最大应力是负相关，D1对最大应力的影响大于 D2，R对减小最大应力有很大的影响。最后，给出了优化后的尺寸，这些结论可为今后的曲轴优化提供参考。