基于疲劳损伤谱的随机振动试验方法在智能电表模拟公路运输中的研究

唐利涛，杨舟，李刚，蒋雯倩

（广西电网有限责任公司电力科学研究院，南宁530023）

智能电表内部元器件繁多，结构精细，包含大量芯片、晶体振荡器、电池、电感及电阻器件，对振动十分敏感。当智能电表在公路路面上运输时，由于路面高低不平而产生随机振动[1-2]，会导致电子器件的性能参数发生变化，从而使工作点移动或造成测量精度下降，影响电表的性能，甚至导致失效。

由智能电表典型寿命剖面可知，运输作为整个寿命周期的初试阶段，其运输过程中的振动应力会对智能电表造成一定损伤[3-5]。因此，无论是在安装使用之前，还是在进行工作状态下的可靠性实验前，合理安排公路运输振动环节都是非常必要的，这有助于增加智能电表在全寿命周期内的可靠性。

公路运输振动是一种宽带、低频的随机振动，且幅度较低、持续时间较长。虽然将智能电表进行跑车实验能够较为真实地反应其经历的振动环境，具有较高的准确性，但是消耗的时间、人力和物力过大，而在实验室内进行模拟振动试验可以实现时间的压缩，使其达到相等的疲劳损伤程度，较为真实地还原所受的振动应力。工程上达到等效疲劳损伤的常参照美军标或国家标准中规定的提高振动量级方法来加速试验，该方法适用于大多数的产品，但对于某一特定产品来说精度可能略有不足。文中介绍一种基于疲劳损伤谱的等效疲劳损伤的振动试验方法，可通过采集真实振动数据或使用类似数据，对其绘制疲劳损伤谱，并根据疲劳损伤谱对试验加速。

1 疲劳损伤谱的概念

疲劳损伤谱是一种与冲击响应谱类似的谱，但其描述的是疲劳损伤与频率之间的关系。对于一个实际的物理系统，可以分解为多个不同的单自由度系统，对于每个单自由度系统，结合S-N曲线及线性疲劳累积理论进行疲劳损伤分析得到损伤，然后与它的固有频率构成一个数据点。这样将多个线性单自由度系统得到的数据点以光滑曲线链接，便可以得到整个系统的疲劳损伤谱。

实际中，对物理模型进行拆分是非常困难的，甚至是不可能完成的，为了更方便得到疲劳损伤谱，需要对模型进行简化。即将多个单自由度系统中的最低频率f1取出，分析该频率对应的系统的疲劳损伤D1，然后改变f1为f2，其余条件不变（ξ和b不变）得到损伤 D2，以此类推重复上述步骤。当频率由 f1遍历至fn，便可以得到整个系统的疲劳损伤D1至Dn，将（fi, Di）用光滑曲线连接起来，便可以得到整个系统的疲劳损伤谱[6-7]。

2 获得疲劳损伤谱的方法

获得疲劳损伤谱主要有两种方法，分别为基于时域的方法[8-9]与基于功率谱密度的方法[10-11]，视振动的不同类型而定。

2.1 基于时域的方法

若随机振动为非平稳振动或非高斯振动，可以通过时域方法来得到其功率谱密度。时域中的疲劳损伤谱的计算与冲击响应谱开始的方式相同，首先获得非平稳环境下的加速度时域谱，通过积分得到位移时间

关系。然后，不同于极限响应谱中寻找峰值响应，通过雨流计数法得到循环，并运行每个响应，以产生循环谱。最后，通过组合线性损伤累计原则和S-N曲线，计算每个频率下的累积损伤（假设疲劳指数 b），并画出损伤-频率曲线，即为疲劳损伤谱。其时域下的计算过程如图1、图2所示。

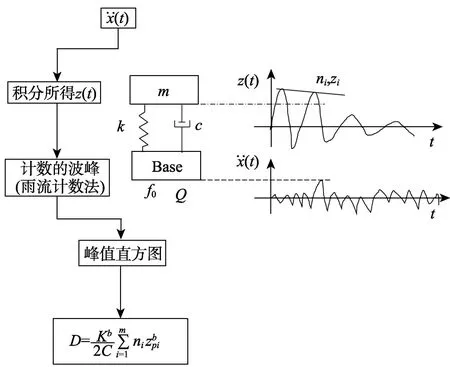
图1 基于加速度时域谱的疲劳损伤谱计算过程

图2 疲劳载荷谱计算原理综述

即使数据采集过程中的噪声是平稳的，不同采集样本中计算所得到的频谱还是会出现差异，尤其对于长时间振动来讲，会存在较大误差。为此，可以通过确定一个平均损伤D(f0,ξ)绘制疲劳损伤谱。

若振动是平稳且各态遍历的，那么可以确定一个具有代表性的时间段 t，并计算 Dt(f0,ξ)，然后通过总的持续时间Θ来估算损伤：

通过这种方法，可以缩短计算时间，并得到相对精确的疲劳载荷谱。

2.2 基于功率谱密度的方法

若采集到的振动信号平稳，且其概率密度服从高斯分布，那么便可以通过其响应峰的概率密度建立峰值直方图，避免了使用较为复杂的计数法。通过功率谱密度来计算疲劳载荷谱的主要过程（如图3所示）为：首先通过加速度的时域谱 ˙x˙ （ t） 计算振动信号的功率谱密度PSD，然后根据功率谱密度计算单自由度系统的相对位移、速度、加速度的均方根值zrms、、。根据上一步的计算结果，计算单位时间的平均频率和平均峰值数值、响应的不规则因子r，确定响应的峰值概率密度，计算系统在自然频率f0处的平均损伤。

图3 基于功率谱密度计算疲劳载荷谱

3 基于疲劳载荷谱的等效疲劳损伤

若根据试验来考察智能电表在公路运输过程中承受随机振动载荷下的可靠度，则必须要保证试验中施加的激励对电表造成的疲劳损伤等效于实际运输过程造成的疲劳损伤，而疲劳载荷谱正是衡量疲劳损伤是否相等的依据之一。

疲劳载荷谱反应的是振动过程中一个频率范围内不同频率对产品造成的损伤，它可以作为一种衡量产品损伤程度的依据。与传统参照标准中的推荐试验量值进行试验的方法相比，使用疲劳损伤谱能够更精确地保证产品在每个试验频率范围中受到的损伤与实际情况相同，这种情况下试验便是行之有效的，且具有用时短、耗费少、试验精准的优点。因此，保证试验中产品的疲劳载荷谱等同于实际运输过程中的电表的疲劳载荷谱，那么该试验方法便是有效的。

由上述过程可知，在疲劳损伤谱不变的情况下，可以通过增大激励幅值来缩短试验时间，以达到加速试验，减少人力、物力消耗的目的。

4 用于加速试验的功率谱密度

对于智能电表的模拟公路运输振动试验，首先要在实际运输过程中采集其真实振动响应。为了减小试验过程中的误差，可以在不同时间或天气下进行 m次（2至3次即可）跑车试验，并记录每次跑车试验中的多个智能电表的振动信号，计算得到疲劳载荷谱FDSm1至 FDSmn，则用于加速振动试验的有效疲劳载荷谱 FDSeff可表示为：

因该有效功率谱密度 FDSeff是基于理想条件下的统计结果得到的，为了保障试验的精度，需要计算一个统计安全系数。这个系数考虑了不同智能电表及其包装之间施加载荷与疲劳强度的变化，如图4所示。

这里假设概率服从高斯正态分布，则安全因子k表达方式为：

图4 安全系数k

设进行加速度后的试验时间为treduced，则应对试验件施加激励的功率谱密度可由计算疲劳损伤谱密度反向求得：

由此，可以得到基于疲劳载荷谱的等效疲劳加速试验的输入激励。该激励以功率谱密度表示，通过随机控制系统进行编辑，并转化为模拟信号，由功率放大器进行放大，输出到激振设备，便可以对产品进行振动试验。

5 方法算例

为对该方法进行说明，选取某型号智能表的随机振动试验功率谱密度量值，使用疲劳损伤谱对其进行加速，并将加速前后的疲劳累计进行对比。由此说明该方法在随机振动试验中的可行性，并展示其耗时短、加速明显、精度精确的优点。

某型号智能电表模拟公路运输试验的振动谱见表1，其运输方式为高速公路卡车运输。对于智能电表的三个轴向，每个轴向按此功率谱密度振动需82.5 min，试验时间依旧过长。为了减小成本消耗，使用疲劳损伤谱对其进行加速，目标试验时间为每个轴向20 min，共计1 h完成试验。对表1中的功率谱密度绘制疲劳损伤谱，如图5所示。

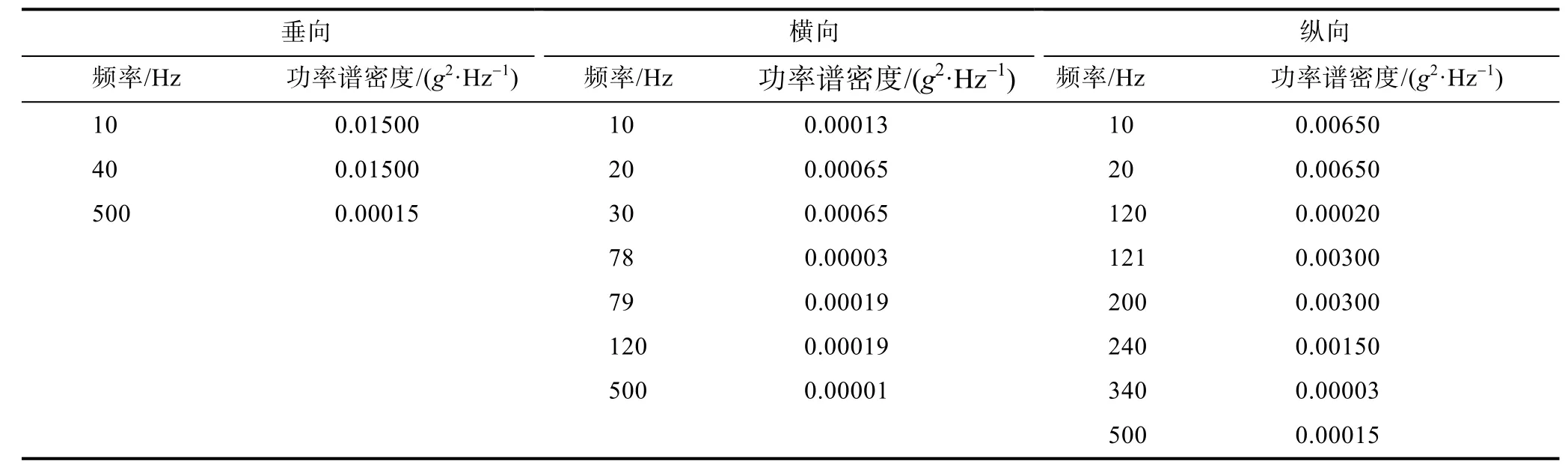
表1 随机振动试验功率谱密度

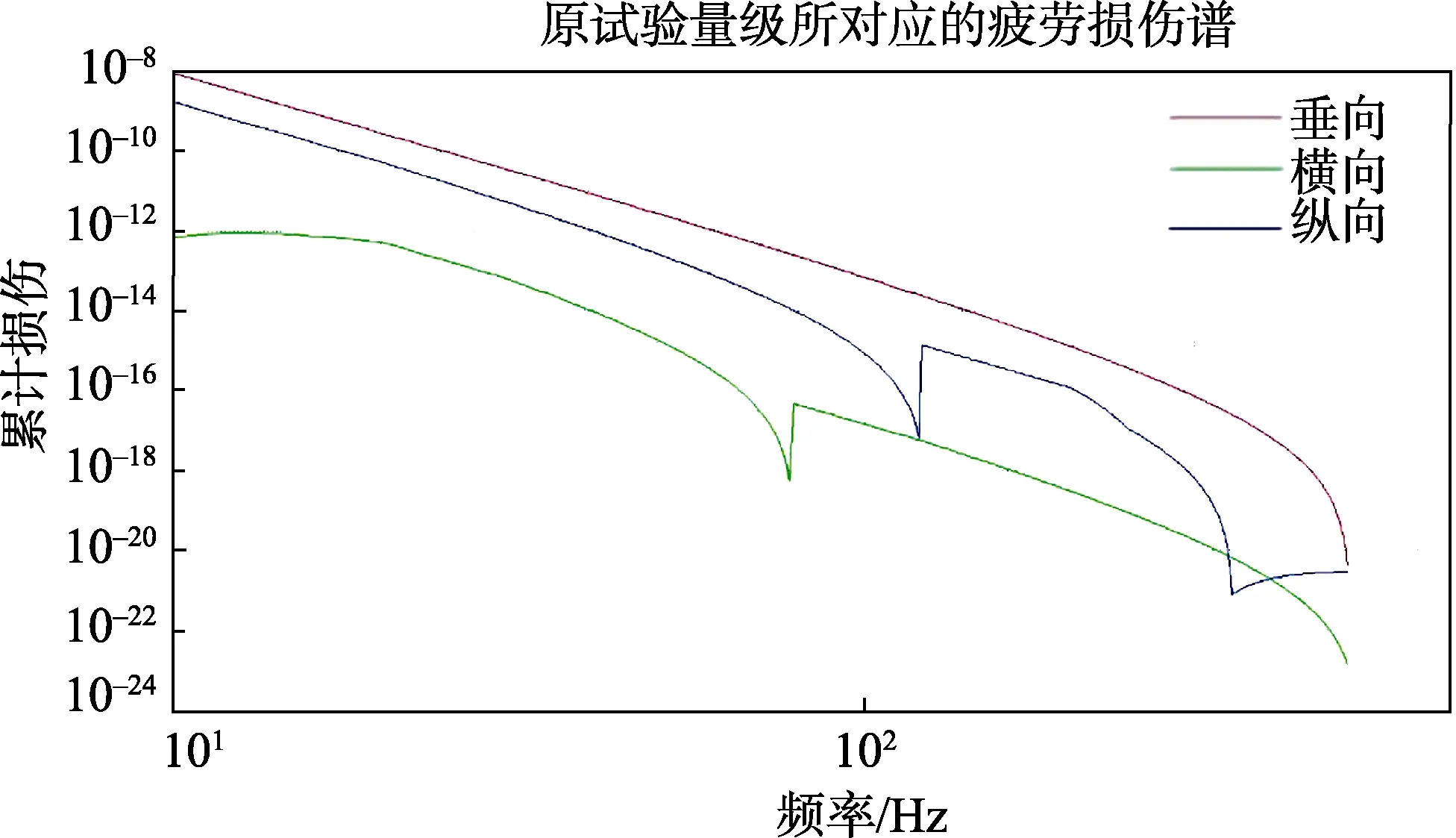
图5 原振动量级疲劳损伤谱

由式（5）可知，设进行加速度后的试验时间为treduced，则应对试验件施加激励的功率谱密度可由计算疲劳损伤谱密度反向求得。对于线性单自由度系统：

且N=fT，则：

美军标MIL-STD-810中建议n=2.4，这里采用该标准对振动试验进行加速。已知原试验量级试验时间treal=82.5 min/轴，加速后试验时间为treduced=20 min/轴，则可知加速振动试验的功率谱密度为：

即用于智能电表随机振动试验的功率谱密度见表2和图6。

为了进行对比，加速前后的疲劳损伤谱如图 7所示。其中，实线为使用标准中的试验谱进行试验所累计的疲劳损伤，虚线为对试验谱进行加速后所累积的疲劳损伤，两者误差为6.4%，不但能够满足工程需求，同时能够节省大量人力、物力资源。

表2 加速后随机振动试验功率谱密度

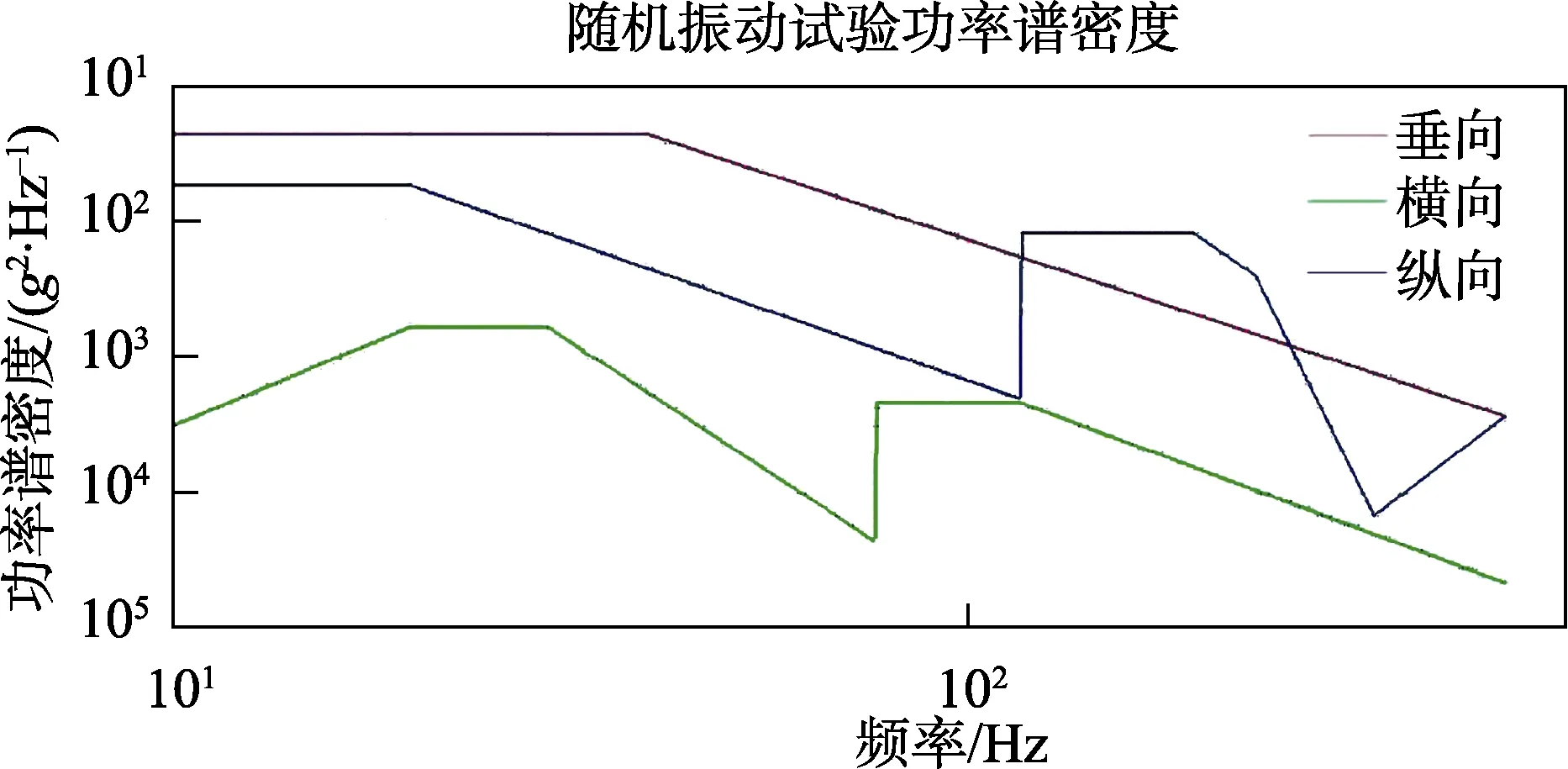
图6 加速后随机振动试验功率谱密度

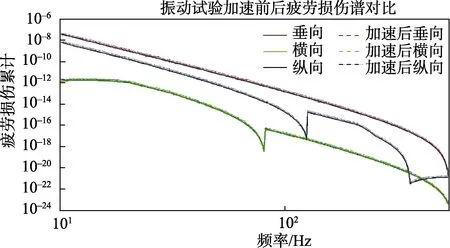
图7 振动试验加速前后疲劳损伤谱对比

6 结语

采用基于疲劳损伤谱的试验方法与传统方法相比，是一种更加全局、系统化的方法。文中据此提出了智能电表模拟公路运输的振动加速试验方法，在保障试验可靠度的同时，可以大幅加速试验，减少物力、财力的消耗。同时，该方法不仅局限于公路运输过程中的振动试验，还可以推广到铁路、水路、喷气式飞机运输中振动的研究，具有广泛的参考价值。