平面四杆机构在舰载垂直发射装置舱口盖系统中的应用分析

刘永亮，任克亮，马旭轮，张基明

（中国船舶重工集团公司第七一三研究所，郑州 450015）

舱口盖系统是舰载垂直发装置的重要组成部分， 既要满足开关盖的技术性能要求，又要在波浪等外载荷的作用下满足刚强度要求[1]。新型超音速导弹要求垂直发射装置有高的贮弹密度和机动性、快的瞬时反应能力，客观上要求舱口盖系统开关盖时间短、反应快、耗能小、可靠性高。

目前垂直发射装置的舱口盖系统主要分为液压式和机电式两大类别。其中液压式舱口盖系统受航区、季节、气候、海况的影响，对液压启闭系统的可靠性要求非常高[2]。在极端情况下，液压系统存在脉动冲击、液压油泄漏等不利因素，影响到舱口盖系统密封的安全性。

平面四杆机构作为一种常见的机械式传动机构，可以方便地实现较复杂的运动。在连杆机构中，可以传递较大的动力。可以得到不同的传动比，实现不同运动规律的要求，便于加工，且生产成本低。

作为一项关键技术，文中提出采用平面四杆机构电动开盖的方式，来实现舱口盖的快速开启和关闭，并通过计算、仿真和试验对舱口盖的技术性能进行摸底。

1 主要性能指标

舰载垂直发射装置带有发控设备，对舱口盖系统发出操控指令，完成舱口盖动作。有以下主要性能指标：

1）自收到发控设备“舱口盖打开”指令到控制设备给出“舱口盖打开好”信号，时间不超过3 s。

2）舱口盖开启角度（甲板面夹角）应大于93°。

2 理论计算

舱口盖开盖解锁机构分为开盖机构和解锁机构两部分[3-10]：开盖机构为平面四杆机构中的曲柄摇杆机构，解锁机构为平面四杆机构的曲柄滑块机构。两机构通过凸轮拨盘实现联动，其动力由一台低速大扭矩电机提供，弹舱盖开盖解锁机构循环完成的动作顺序是：解锁、开盖、关盖、上锁。

根据舱口盖功能要求，确定开盖机构曲柄摇杆机构各构件的长度及其传动比，进行负载分析，完成电机的转速及输出转矩计算。然后运用机械系统仿真软件ADAMS进行计算机仿真。

2.1 确定各构件的长度及传动比

考虑装置上所提供的安装空间，最终选用下面的曲柄摇杆机构来实现传动，其运动分析如图1所示。机构中两个死点位置位于同一直线上，即图1中所示的C1和C2点。其中，曲柄为杆CD；摇杆为杆AB；机构中 AB1C1D位置表示舱口盖关闭到位；AB2C2D位置表示舱口盖开启到位。曲柄CD转动幅度为180°，摇杆AB转动幅度为95°。

四杆机构的主要设计参数分别为：AB= 94.85 mm，BC=241.88 mm，CD=70 mm，AD=250.2 mm，θ=28.78°，CD+AD＜AB+BC，满足杆长条件。

随着舱口盖开启角度α的改变，舱口盖连杆机构瞬时传动比也在改变。用 C语言编制相应的计算程序，可以计算出舱口盖开启角度α所对应连杆机构瞬时传动比的数值解，如图2所示。

图2 舱口盖连杆机构瞬时传动比曲线

由曲线可以看出，在接近两个死点位置附近，传动比非常大，在中间位置最小。根据工程应用实际情况，假设曲柄作匀速转动，其角速度为常数。则摇杆即舱口盖的转动角速度的变化趋势为：启动时角速度从0加速到最大，然后减速至终点时为0。在初始位置和终点位置的速度均近似为0，这种变化对开盖是有利的。

2.2 负载分析

由开盖过程可以看出：负载转矩随开启角度的变化而变化，如图3所示。

负载转矩计算：

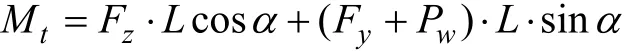
图3 舱口盖受力

式中：Pw为风载荷，N；Fy为 y方向摇摆过载力；Fz为z方向摇摆过载力。

由此可见，负载转矩随舱口盖开启角度的变化而变化，不是常数。

利用计算机编程求解出舱口盖开启角度负载转矩的数值解。由数值解可以看出，负载转矩在弹舱盖开启约5°时，达到其最大值Mmax=812.7 N·m，如图4所示。

图4 舱口盖负载转矩曲线

2.3 确定所选用电机输出扭矩和转速

1）电机输出扭矩。因为动能的增量必须≥0，从能量角度来说，必须满足W驱≥W负（不考虑摩擦、机械损失），即：

式中：M为电机输出扭矩，N·m；Mt为负载转矩，N·m；为机构传动比。

电机输出扭矩不小于机构传动比与负载转矩的乘积，用C语言编制相应的计算程序进行计算，电机转矩M应满足：M≥569 N·m。

2）电机转速。电机转速主要由开盖时间和机构传动比确定。开盖时间小于3 s，电机转动180°后弹舱盖开启到位，电机转速n应满足：n≥10 r/min。

3 仿真分析

3.1 模型假设

通过对四杆机构的运动分析，作出如下假设：

1）按机构运行情况对各构件分配质量及转动惯量。

2）各构件之间可以相互转动。

3）各杆件连接处在传动过程中，运动副无相对运动。

4）忽略各杆件连接处在传动过程中的摩擦力和磨损情况。

5）忽略各部件之间的装配误差，不考虑其他因素对系统的影响。

3.2 结构描述

四杆机构的拓扑关系如图 5所示。机架通过 f1转动副与曲柄一端联接，曲柄一端通过f2转动副与连杆一端联接，连杆一端通过f3转动副与摇杆联接，摇杆一端通过f4转动副与机架联接。整个系统可以进行平面运动，共9个自由度。

图5 结构拓扑图

3.3 动力学模型

根据动力学模型可导出系统总动能T，总势能V，总耗散能D，它们均为系统的结构参数与广义坐标的函数。由拉格朗日方程得：

x=x(x1,x2,x3…)最后得系统运动微分方程：

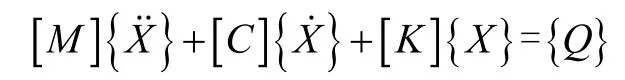
式中：[M]、[C]、[K]分别为994阶量矩阵、阻尼矩阵和刚度矩阵；X、X˙、X˙˙分别是广义坐标的位移向量、速度向量和加速度向量；{Q}为广义力向量。

3.4 仿真过程及结果分析

本次仿真环境是在软件 ADAMS/View环境中进行的[11]，在驱动连杆的旋转副上加角速度驱动。在作用对象的连杆上加上负载。仿真模型及开盖所需扭矩如图6和图7所示。从图5中可以看出，开盖所需的扭矩大于550 N·m，与理论计算值所得的扭矩不小于569 N·m基本一致，只要电机输出扭矩大于569 N·m就能满足开盖所需动力要求。

图6 舱口盖开盖机构仿真模型

4 试验及结果

对机构进行开盖试验，试验过程中，反复执行开关盖动作数次，记录下每次开盖时间和开盖角度以及机构运行情况，见表 1—4。为验证所选用电机的功率是否满足要求，通过加配重块来模拟风载荷及摇摆载荷，每个配重块质量为30 kg，共3块，每加一块配重块做10次。从表1—4中可以看出，配重块对每次开盖时间和开盖角度影响不大，每次开盖时间均小于3 s，开盖角度均大于93°，且机构运行正常[12-15]。因此开盖时间和开盖角度均满足舱口盖系统主要性能要求。

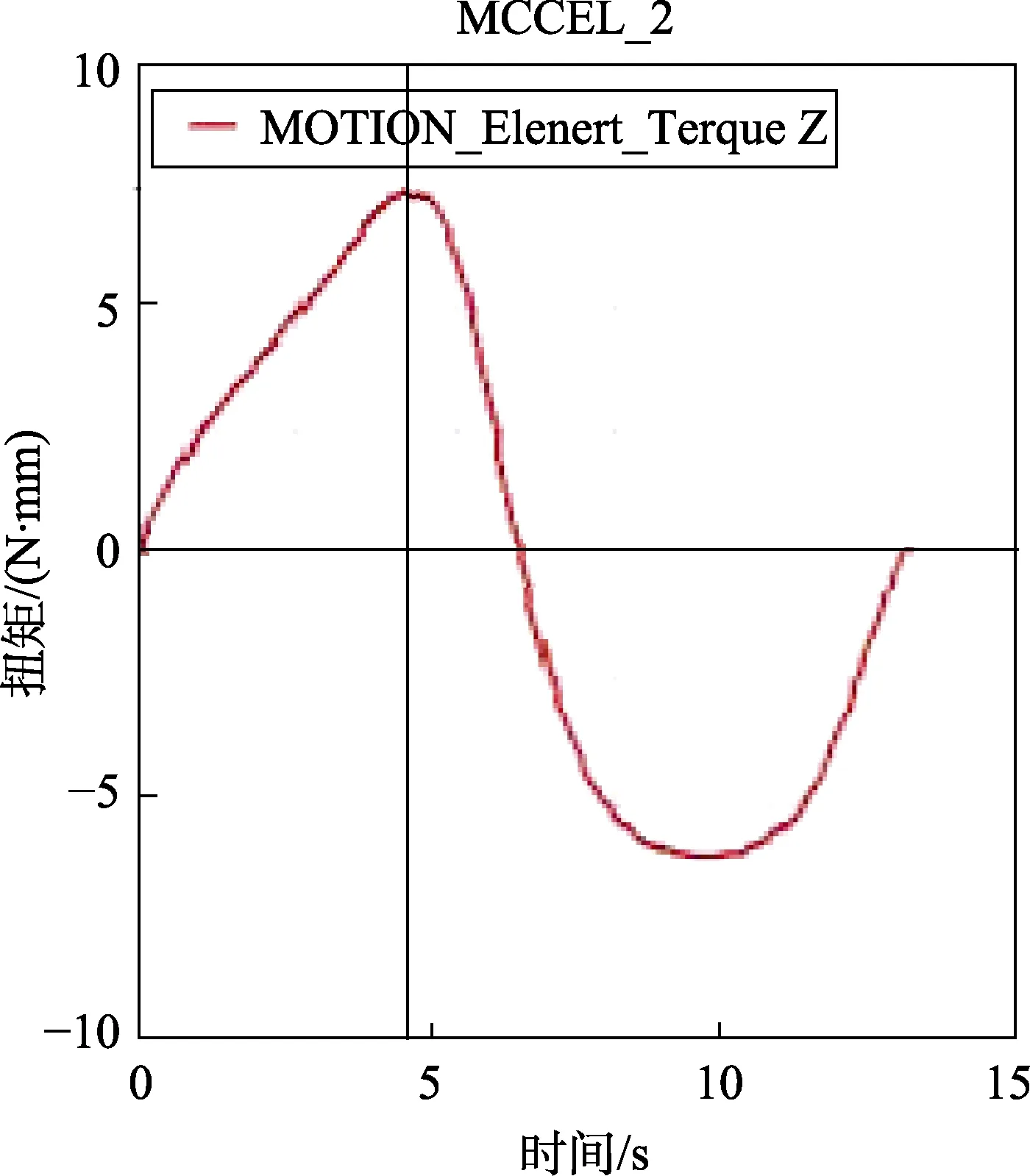
图7 舱口盖开盖机构所需扭矩

表1 不加负载开盖情况

表2 30 kg负载开盖情况

表3 60 kg负载开盖情况

表4 90 kg负载开盖情况

5 结论

四杆机构的设计满足舱口盖系统的主要技术指标要求。通过试验验证了舱口盖系统方案设计可行，运行可靠，实现了快速开盖的战术指标要求，可为其他垂直发射装置的舱口盖设计提供工程经验。