基于状态量扩维的旋转式捷联惯导系统精对准方法

叶文， 翟风光， 蔡晨光， 李建利

(1. 中国计量科学研究院力学与声学计量科学研究所, 北京 100013；2. 北京航空航天大学仪器科学与光电工程学院, 北京 100083)

旋转式捷联惯导系统(Strapdown Inertial Navigation System,SINS)在不使用外部信息的前提下，利用转位机构带动惯性测量单元(Inertial Measurement Unit，IMU)以一定的旋转方案转动，将陀螺和加速度计的常值误差调制成周期性变化的形式，从而实现惯性器件误差的自动补偿，提高系统长时间导航性能[1-4]。但是，旋转调制无法抑制初始对准误差对导航精度的影响。而初始对准是惯性导航的关键技术之一，其精度直接决定了系统导航精度[5]。因此，对旋转式捷联惯导系统初始对准的研究显得尤为重要。

现有旋转式捷联惯导系统静基座精对准多采用传统捷联惯导系统的对准方法，文献[6-8]在旋转过程中利用卡尔曼滤波进一步估计系统初始姿态，但未分析旋转过程中系统各状态量可观测度变化；文献[9-12]建立滤波模型后，分析了转动过程中各状态量可观测度变化，但是状态模型仍采用静基座精对准模型，未分析旋转过程陀螺和加速度计标度因数误差、安装误差是否可观测。

旋转式捷联惯导系统通过周期性旋转改变了系统状态变量的可观测性[13-14]，而现有旋转式捷联惯导系统对准模型多采用静态10维对准模型，未对旋转过程中陀螺和加速度计的标度因数误差、安装误差的可观测性进行分析，便将其从状态变量中剔除，导致滤波模型不精确，进而影响了姿态对准精度。针对此问题，本文提出了一种基于状态量扩维的旋转式捷联惯导系统精对准方法。首先，建立28维精对准模型；然后，通过可观测度分析优化精对准模型；最后，通过仿真试验验证了该方法的有效性。

1 扩维的精对准模型

静基座下载体的位置是已知的，不考虑载体位置变化，建立静基座初始对准的状态方程为

(1)

式中：X为状态向量；A为状态转移矩阵；B为系统噪声扰动矩阵；W为零均值高斯白噪声。

传统旋转调制精对准模型中，状态变量X为10维，包括水平速度误差、失准角误差、水平加速度计常值零偏、三轴陀螺常值漂移，如下：

εxεyεz]T

(2)

状态转移矩阵和系统噪声扰动矩阵为

(3)

式中：

(4)

(5)

选取2个水平速度误差δVE、δVN作为观测量，静基座下载体位置未发生变化，外观测量为零。量测方程为

Z=HX+V

(6)

陀螺和加速度计的测量误差是影响系统精度的主要因素，因此必须对其进行精确建模。但传统的旋转式捷联惯导系统静基座对准模型为10维，陀螺和加速度计的标度因数误差以及安装误差可通过标定获得，但是标定补偿后仍然会存留残余误差，因此10阶系统误差模型不能满足导航系统的需求。基于上述思想，在传统10维的对准模型基础上，将陀螺和加速度计的标度因数误差和安装误差扩展为状态变量，建立旋转式捷联惯导系统的28维精对准模型。

陀螺的误差模型为

(7)

式中：δωgx、δωgy、δωgz为陀螺输出误差；ωx、ωy、ωz为陀螺输入；δKgx、δKgy、δKgz为陀螺标度因数误差；Egxy、Egxz、Egyx、Egyz、Egzx、Egzy为陀螺安装误差。

将式(7)表示成矩阵形式为

δωg=[δKg+Eg]ω+ε

(8)

式中：

加速度计的误差模型为

(9)

式中：δfax、δfay、δfaz为加速度计输出误差；fx、fy、fz为加速度计输入；δKax、δKay、δKaz为加速度计标度因数误差；Eaxy、Eaxz、Eayx、Eayz、Eazx、Eazy为加速度计安装误差。

将式(9)表示成矩阵形式为

(10)

式中：

扩充后的系统状态变量为

εzδKgxδKgyδKgzEgxyEgxzEgyxEgyz

EgzxEgzyδKaxδKayδKazEaxyEaxzEayx

EayzEazxEazy]T

(11)

A阵发生变化，如下：

(12)

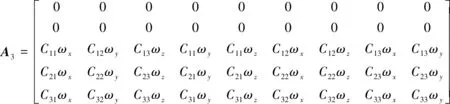
(13)

(14)

系统量测量不变，量测矩阵H变为

(15)

在旋转式捷联惯导系统28维的精对准模型中，各状态变量在转动的过程并不是完全可观测的，因此利用系统可观测度分析理论对各状态变量可观测度进行分析。

2 系统可观测度分析

旋转式捷联惯导系统的航向角由于旋转不断发生变化，此时系统是时变的，因而可用分段线性定常系统(Piece-Wise Constant System，PWCS)来分析旋转过程中的可观测性，判断各状态变量是否可观测。

由于系统的可观测性与激励无关，为简化分析，只研究齐次系统的可观测性。系统状态方程和量测方程离散化后对应的齐次方程为

(16)

系统总体可观测性矩阵(Total Observability Matrix，TOM)为

(17)

(18)

由文献[15]可知，可用Qs(r)代替Q(r)进行系统可观测性分析。

PWCS只能定性分析状态变量能否被观测，无法确定某一状态变量在不同时间段内的可观测程度。因此PWCS在可观测性分析基础上，进行基于奇异值的系统可观测度分析，求出奇异值大小，从而确定各状态变量的可观测度。下面利用奇异值分解对系统的可观测度进行分析。

将矩阵Qs(r)进行奇异值分解，可得

(19)

式中：U=[u1u2…um]；V=[v1v2…vm]；

由Z=Qs(r)X0可得

(20)

(21)

式中：Z为量测量；X0为系统初始状态。

如果观测量具有常值范数，那么初始状态值可以形成一个椭球，其方程为

(22)

取αi=1/σi，则式(22)可表示为

(23)

式中：αi为椭球的主轴长度。可知奇异值越大，αi越小，椭球体积越小，对初始状态的估计程度越高。第i个状态变量对应的可观测度ηi可表示为

(24)

本文采用单轴方位连续旋转调制系统，其转速为6(°)/s，航向角变化步长为60°，分析其静止时间段(0～10 s)和转动过程(第一时间段：10～20 s;第二时间段：20～30 s)中各状态变量可观测性变化，其中的各状态变量对应奇异值变化如表1所示。

由表1可知，静止状态下陀螺和加速度计的标度因数误差、安装误差奇异值较小，可观测度低，故传统10维模型中不考虑陀螺和加速度计的标度因数误差、安装误差。在旋转过程中，陀螺和加速度计标度因数误差、安装误差奇异值增大，可观测度变大，尤其是陀螺的标度因数误差δKgx和安装误差Egxz、Egyz3个状态变量对应的奇异值大小有了明显改善，其中δKgx对应的奇异值从静止时间段的7.51×10-39提高到2.15×10-3，Egxz、Egyz对应的奇异值从静止时间段的6.45×10-34、1.44×10-31提高到第二时间段的2.70。可知，旋转过程中δKgx、Egxz、Egyz可估计程度得到了显著提高。

表1 各状态量对应的奇异值变化Table 1 Singular value change of state variables

3 改进的13维精对准模型

由于不可观测的状态变量对系统精度影响较小，因此根据系统各状态变量可观测度分析结果，去掉28位精对准模型中不可观测的状态变量，包括加速度计安装误差、标度因数误差以及陀螺的标度因数误差中的δKgy、δKgz和安装误差中的Egxy、Egyx、Egzx、Egzy，保留陀螺的误差项δKgx、Egxz、Egyz。此时系统状态变量变为13维，如下：

εyεzδKgxEgxzEgyz]T

(25)

此时矩阵A阵变为如下形式：

(26)

(27)

系统量测量保持不变，量测矩阵H发生变化，如下：

(28)

4 仿真试验

仿真条件设置如下：状态变量X的初始值均为零，陀螺常值漂移为0.2(°)/h，随机漂移为0.04(°)/h；加速度计常值零偏为100 μg，随机零偏为25 μg；陀螺的标度因数误差为100 ppm(ppm为百万分之一，是惯导标度因数的通用表示方法)，安装误差均为1×10-5(°)；速度测量误差为0.01 m/s；初始姿态为零；初始失准角φE、φN、φU分别为0.1°、0.1°、0.5°；地理纬度为40°，经度为116°。协方差阵初始值P(0)、系统噪声阵q、量测噪声阵R初始值如下：P(0)=diag{(0.01 m/s)2,(0.01 m/s)2,(0.1°)2,(0.1°)2,(0.5°)2,(100 μg)2,(100 μg)2,(0.2(°)/h)2,(0.2(°)/h)2,(0.2(°)/h)2,(1×10-4)2,(1×10-5)2,(1×10-5)2},q=diag{(25 μg)2,(25 μg)2,(0.04(°)/h)2,(0.04(°)/h)2,(0.04(°)/h)2},R=diag{(0.01 m/s)2,(0.01 m/s)2}。

仿真试验结果如图1所示。可以看出，本文方法提高了航向角的收敛速度。统计500 s以后载体姿态的均方根误差(Root Mean Square Error，RMSE)，如表2所示。

从表2可以看出，本文方法得到的航向角误差为0.022 4°，而传统方法得到航向角误差为0.031 4°，精度提高了约29%。且俯仰角和横滚角估计精度也有小幅提升。

从图2可以看出，本文方法估计出的水平陀螺常值漂移分别为0.19(°)/h、0.20(°)/h，而同样条件下传统方法得到的水平陀螺常值漂移分别为0.17(°)/h、0.18(°)/h，水平陀螺常值漂移的估计精度得到提高，同时可以看出水平陀螺和天向陀螺收敛速度加快。

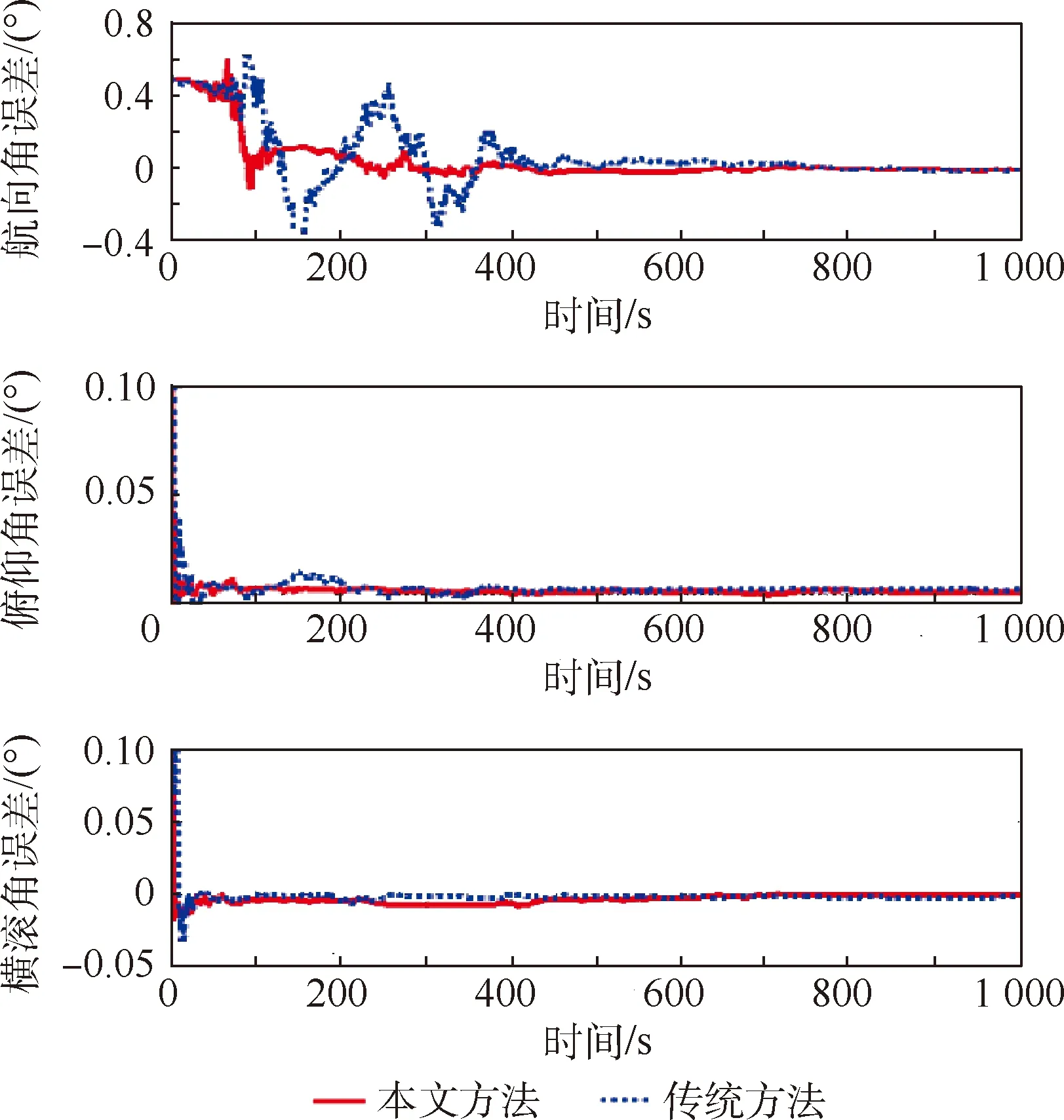
图1 姿态角误差估计Fig.1 Estimation of attitude angle errors

方法航向角误差俯仰角误差横滚角误差传统方法0.03140.00170.0019本文方法0.02240.00110.0012

图2 水平陀螺常值漂移估计Fig.2 Estimation of horizontal gyroscope constant drift

从图3可以看出，本文方法的水平加速度计常值零偏估计分别为81 μg、87 μg，而传统方法精对准下分别为71 μg、73 μg，水平加速度计常值零偏的估计精度有明显提高。

从图4可以看出，本文方法可估计出陀螺的标度因数误差δKgx和安装误差Egxz、Egyz。仿真条件设置的δKgx为100 ppm，估计出的δKgx为178ppm；设置的Egxz、Egyz为1×10-5(°)，估计出的Egxz、Egyz分别为8.08×10-6(°)、4.11×10-6(°)。

图3 水平加速度计常值零偏估计Fig.3 Estimation of horizontal accelerometer constant null bias

图4 陀螺的 δKgx及Egxz、Egyz估计Fig.4 Estimation of δKgx,Egxz and Egyz of gyroscope

5 结 论

1) 考虑了陀螺和加速度计的标度因数误差、安装误差，扩展为28维的精对准模型。

2) 对旋转过程各状态变量的可观测度变化进行分析，将精对准模型优化为13维。

3) 仿真结果表明，与传统方法相比，本文方法航向角对准精度提高了约29%，且提高了水平陀螺常值漂移、加速度计常值零偏估计，同时还可估计出δKgx及Egxz、Egyz。

4) 如何在系统绕双轴或者三轴旋转时进行对准并进一步提高陀螺和加速度计的误差参数估计精度将是今后的研究方向。