分数算子的Charef有理逼近与新颖标度方程的奇异性质

谢雨婧， 袁 晓

(四川大学电子信息学院， 成都 610064)

1 引 言

近年来，分数微积分的概念在数学之外，特别是物理、化学、生物、工程等领域的应用激起了人们相当大的关注，并发现使用分数微积分比整数微积分更能精确描述或建模实际的问题[1]. 分抗元(Fractor，有时人们简称分抗)是一种能实现分数阶积分或微分运算的新电路元件，并使用符号F表示，理想μ阶分抗元的阻抗(或导纳)为

I(μ)(s)=F(μ)sμ, 0<|μ|<1

(1)

式中，s=σ+jΩ是复频率变量(也称为运算变量)；μ是运算阶；sμ称为μ阶微积分算子，简称分数算子. 常量F(μ)是分抗元的电路集总特征值，简称分抗值(Frac-tance). 分抗元越来越广泛地应用到电路设计中[2,3]，且已形成分数阶电路与系统的研究方向. 由于理想的分抗元件不存在，人们通过对各种分数阶现象与过程的观察，构建了许多在一定频率范围内实现半阶分抗的无源分抗逼近电路.该电路利用可实现的无源整数阶元件(电阻，电容，电感)构造二端网络，特别是(RC网络)来逼近理想分抗元[4,5]，此类无源网络称为分抗逼近电路.通过对分数微积算子、分抗与分抗逼近电路及其运算特征分析[6,7]，可将电路的分数微积分运算性能，通过标度拓展或非正则标度方程拓展至任意阶分数算子的有理逼近[8,9].

许多物理现象，包括某些类型的电噪声、介质中极化阻抗的弛豫行为和音乐的谱密度，表现出与频率有关的分数次幂函数，或等效的对数-对数波德图上的分数斜率，这类过程可称为1/f型过程或分形系统[10]，表示为

(2)

在大多数情况下，系统通常在低频段(0←Ω<Ωτ)处表现出有限的幅值. 因此，一些研究者通过Pade近似表示单分数幂极点(Single-Fractional Power Pole)函数，描述分形系统的频率现象[11]. 文献[12]描述了由无源R和C恒相元件组成的梯形网络模型来表示(2)的函数. 由此，Charef等提出描述分形系统的一种由若干零极对级联分支组成的奇异函数方法[13](又称Charef有理逼近)，Charef有理逼近使用适当的有理传递函数来描述分数阶系统. 文献[14]给出了分数PID控制器的有理函数和模拟电路实现，通过例子说明了该方法的有效性. 分数算子的Charef有理逼近是一种使用比较广泛的有理逼近方法，在分数阶混沌系统和分数阶控制系统等[15,16]方面应用较多. Zourmba等[17]利用Charef逼近方法近似传递函数用于实现小数积分电路单元，该模型比现有模型需要的组件更少，并且供了更高的精度.

本文根据单分数幂极点与单分数幂零点(Single-Fractional Power Zero)模型的奇异传输函数，利用Charef有理逼近法的零极点组合逼近，引入两个非正则的标度方程——新颖标度方程来表征Charef有理逼近的极限情形. 探究新颖标度方程迭代获得的有理函数序列的运算有效性、运算性能和零极点分布，最后得到与典型标度方程不同的新颖特性.

2 Charef有理逼近与新颖标度方程

2.1 单分形的奇异结构

μ阶单分数幂极点与零点系统的传输函数在复频域分别表示为[11]

(3a)

HZ(s)=(1+s/pτ)μ, 0<μ<1

(3b)

令w=τs(称为归一化运算变量)，其中τ=1/pτ为松弛时间常数. 对单分数幂极点传输函数(3a)式与幂零点(3b)传输函数归一化后分别得

(4a)

yz(w)=(1+w)μ

(4b)

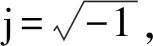
ΛP(ϖ)=lg|HP(j·10ϖ)|=-μlg|1+j·10ϖ|

(5a)

ΛZ(ϖ)=lg|HZ(j·10ϖ)|=μlg|1+j·10ϖ|

(5b)

在ϖ→±∞的极限情况下，幅频特征函数ΛP(ϖ)/ΛZ(ϖ)分别趋近于两条渐进直线.

(6a)

(6b)

根据式(5)和式(6)可知，单分数幂极点无理函数的幅频特征曲线可用两条渐近线近似表示(如图1所示).

图1 单分数幂极点与零点传输函数的幅频特征曲线及其渐近线Fig.1 Amplitude-frequency characteristic curve and its asymptote of single fractional power pole and zero transfer function

2.2 Charef有理逼近与零极点对子系统

将式(4a)的无理函数yP(w)通过实零极点对形式重写为有理逼近函数，并在有限的频率范围内，可以截断为一个有限的迭代次数k，使用yPk(w)逼近yP(w).

(7)

第i对零极点对(zi,pi)一次子系统的归一化阻抗函数为

(8)

(9)

式(9)中，实数oi表示零点频率指数和实数χi表示极点频率指数[18].令极点与零点之比为

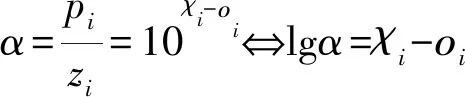
(10)

得一次零极点子系统的频域特征函数:

(1) 幅频特征函数

(11a)

(2) 相频特征函数

(11b)

(3) 阶频特征函数

(11c)

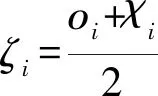
图2a零极点对子系统函数Ei(w)的幅频特征曲线可由一条斜率为-1和两条水平渐近线组成的Z形折线近似表示，是由零点与极点的共同作用导致的.由(10)式可知，lgα取值越大，一次子系统的运算特征的带宽越大[19]. 子系统函数Ei(w)的相频特征ϑi(ϖ)和阶频特征ui(ϖ)具有偶对称性和局域化特性图2b和2c，正是这种每个一次子系统都会产生波峰的局域化特性，使得无理函数序列yP(w)在频域产生准周期性的运算振荡现象，运算振荡现象是所有一次子系统的集体行为[20](3.2节详细分析).

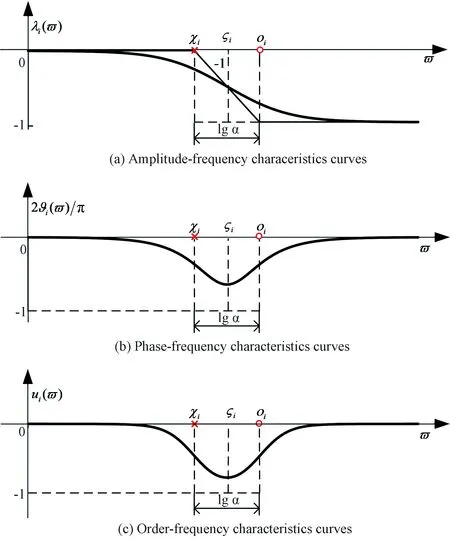
图2 一次子系统的频域特征曲线 Fig.2 Frequency domain characteristic curve of the primary subsystem

2.3 Charef有理逼近过程

根据图1描述的单分数幂极点传输函数yP(w)的幅频特征曲线在波特图中可用两条渐近线近似表示，以及图2描述零极点对子系统函数Ei(w)的运算特征函数，组合可得子系统逼近幅频曲线的过程如图3.

2.4 零极点分布关系

递进因数(Recursive Factors)α,β，标度因子(Scaling Factor)σ，可根据渐进幅频误差δ表示.

α=10[δ/10(1-μ)]

(12a)

β=10[δ/10μ]

(12b)

σ=αβ=10[δ/10μ(1-μ)]

(12c)

当0<σ<1时为反比拓展，当1<σ<∞时为正比拓展[10]. 零点和极点频率以递进分布形式确定，以单分数幂极点的传输函数为例有

(13a)

(13b)

另外，极点pi与前一极点pi-1的位置比等于零点zi与前一个零点zi-1的位置比为

(14a)

(14b)

根据上述公式，可以从第一个极点得到所有的极点和零点，关系如下.

pi=σip0,i=0～k

(15a)

zi=σiαp0,i=0～k-1

(15b)

2.5 新颖标度方程

为了用线性时不变的系统模型表示单分数幂极点与单分数幂零点，需要用有理传递函数来逼近其无理传递函数. 使用Charef等人[14]给出的近似方法，在传输函数的幅频曲线图上使用斜率为-μ的直线近似表示，该渐近线由复平面负实轴上零极点对应的若干条斜率为-1和0的直线构成. 因此给出近似结果，单分数幂极点传输函数yP(w)=(1+w)-μ, Charef-I有理逼近：

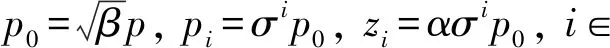
(16a)

单分数幂零点传输函数yZ(w)=(1+w)μ, Charef-D有理逼近：

(16b)

给定一个有理可实现的初始阻抗函数y0(w)=N0(w)/D0(w)，根据式(13)可以构造迭代过程有理函数序列{yΙk(w),k∈+}、{yDk(w),k∈+}，如下式.

(17a)

(17b)

得到两个非正则的新颖标度方程

(18a)

(18b)

3 新颖标度方程的近似求解与真实解

3.1 近似求解与运算有效性

运算有效性是指非正则的标度方程给定初始迭代函数y0(w)的迭代过程

yk(w)=F(ayk-1(σw)),k∈+

(19)

两个非正则新颖标度方程，在高频段可以近似简化为正则标度方程. 对于Ⅰ型新颖标度方程有

(20)

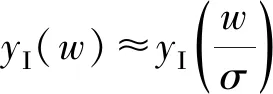
yΙ(w)≈ζΙwμΙ→μΙ=0

(21)

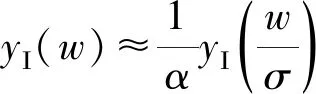
yΙ(w)≈ζΙwμΙ→μΙ=-lgα/lgσ

(22)

由上式可得，Ⅰ型新颖标度方程在高频段具有负分数阶算子.

对于D型新颖标度方程有

(23)

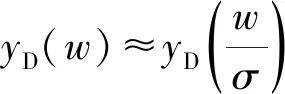
yD(w)≈ζDwμD→μD=0

(24)

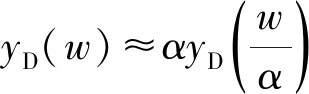
yD(w)≈ζDwμD→μD=lgα/lgσ

(25)

由上式可得，D型新颖标度方程在高频段具有正分数阶算子.

从数学角度分析，新颖标度方程迭代生成的有理函数序列yΙ(w)的运算阶都应在高频段有效，且I型新颖标度方程迭代生成的有理函数序列yΙ(w)的有效运算阶是负任意分数阶，D型新颖标度方程迭代生成的有理函数序列yD(w)的有效运算阶是正任意分数阶. 典型标度方程反比拓展0<σ<1都在高频段有效，正比拓展0<σ<1都在低频段有效[22]. 但两种新颖标度方程的运算有效频段与标度因子σ是正比或反比拓展无关，这与常规拓展标度方程的运算有效性不同，正是新颖标度方程新颖性质的体现.

3.2 新颖标度方程的真实解与运算振荡现象

近似求解可从理论上判断标度方程的运算有效性，真实解可验证近似求解的准确性，有利于直观分析运算性能和逼近性能[23]. 由半阶有效的分抗逼近电路拓展得到的具有可构造任意分数阶运算性能的标度化分抗逼近电路特征. 以I型新颖标度方程为例，给定初始阻抗为yΙ0(w)=1，迭代求得有理阻抗函数序列如下式.

(26a)

(26b)

(26c)

给定合适的标度因子σ，使用Matlab求解式(26)可得有理阻抗函数序列{yΙk(w),k∈+}，对应的运算特征曲线如图4所示.

D型新颖标度方程的有理阻抗函数序列

(27)

对应的阶频特征曲线与相频特征曲线如图6.

观察图4、图5和图6，新颖标度方程迭代生成有理逼近函数存在运算振荡现象[24]，存在固定的振荡周期如下.

图4 正比拓展时I型新颖标度方程运算性能(σ=5, k=10)Fig.4 Operational performance of I-type novel scale equation with proportional expansion(σ=5, k=10)

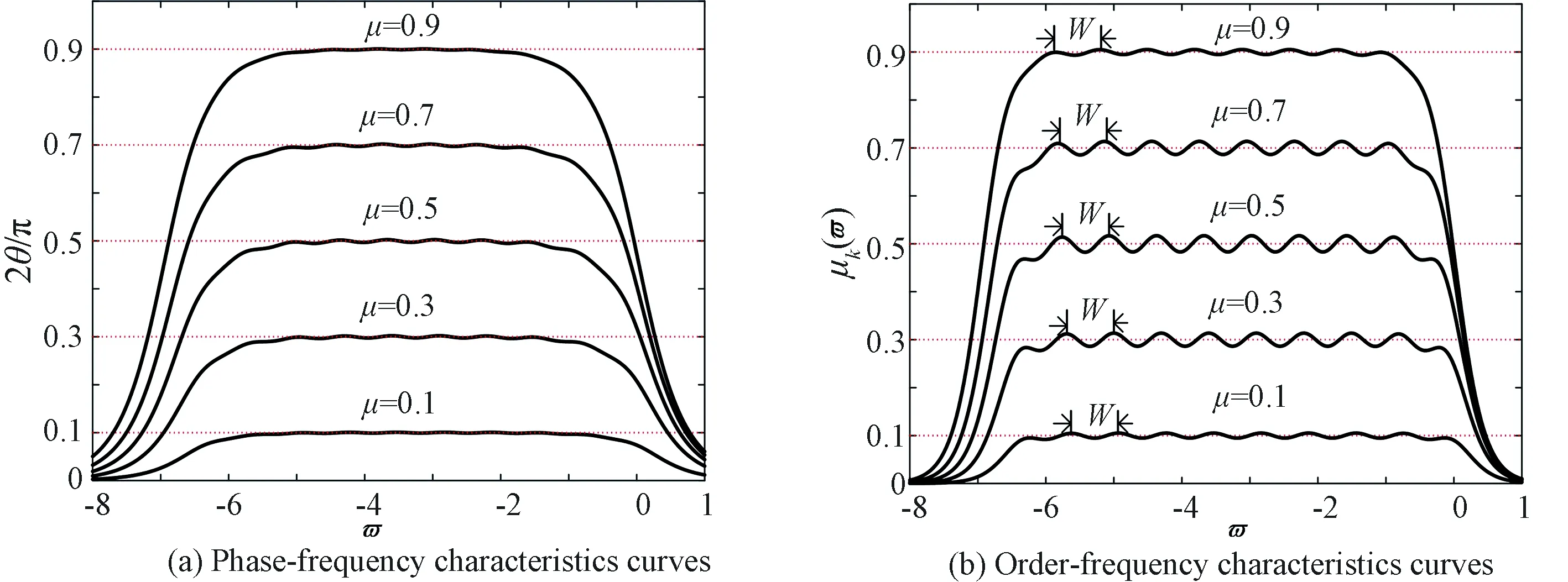
图5 反比拓展时I型新颖标度方程运算性能 (σ=1/5, k=10)Fig.5 Operational performance of the I-type novel scale equation when inversely expanded (σ=1/5, k=10)

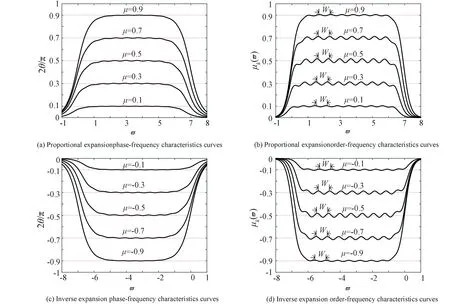
图6 正比和反比拓展时D型新颖标度方程的运算性能 (σ=5, σ=1/5)Fig.6 Operational performance of the D-type novel scaling equation when the proportional and inverse ratios are expanded(σ=5， σ=1/5)

W=|lgσ|,σ≠1

(28)

由于单分数幂极点与零点系统由若干个零极点一次子系统组成，每个零极点子系统Ei(ϖ)都会产生局域化的波峰图(如图2b和2c)，导致有理函数yΙk(w)、yDk(w)在频域产生了准周期的振荡现象. 阶频特征振荡的幅度与标度因子σ和分数算子μ有关.

4 新颖标度方程的奇异性质

有理函数序列yk(w)，取w=j·10ϖ(ϖ是频率指数变量)可得频域特征函数.

yk(j·10ϖ)=Λk(ϖ)exp(j·θk(ϖ))

(29a)

式中幅频特征：

Λk(ϖ)=lg|yk(j·10ϖ)|

(29b)

相频特征：

θk(ϖ)=Arg{yk(j·10ϖ)},ϖ∈R

(29c)

阶频特征：

(29d)

相频特征和阶频特征刻画了分数算子有理迭代过程的运算性能. 以初始阻抗为例，对比I型新颖标度方程在正比与反比拓展条件下的运算性能.

I型新颖标度方程正比拓展(σ=5)迭代次数为10次的数值解与近似求解的理论值一致，在高频范围内实现负任意阶分数算子wu有理逼近如图4b.虚线表示分数算子μΙ=-0.1～-0.9，取值间隔为0.2的理想频域特征曲线，其中α的值是根据近似解(μΙ=-lgα/lgσ)计算得到.

I型新颖标度方程反比拓展(σ=1/5)迭代次数为10次的数值解在高频段不存在分数阶性质，但在甚低频段实现正任意阶分数算子wμ有理逼近如图5b，这与近似求解的理论结果不一致. 反比拓展的数值解无法通过近似求解的理论结果解释，这是新颖标度方程的第二个奇异性质.

D型新颖标度方程与I型新颖标度方程的情况相似，正比拓展(σ=5)高频段正任意分数阶有效图如图6b，反比拓展(σ=1/5)低频段负任意分数阶有效图如图6d.

根据2.4节零极点分布关系的式(12)，画出两种新颖标度方程的零极点分布图，进一步分析反比拓展时数值解与近似解不一致的原因. 分析I型和D型新颖标度方程正反比拓展的零极点分布图. 以I型新颖标度方程正反比拓展为例，根据零极点频率指数oki和xki与零极点的关系式(9), 标度因子正比与反比分别取值σ=5、σ=1/5，迭代次数k=10，令分数阶算子μΙ=-0.1～-0.9，取值间隔为0.2，求得新颖标度方程有理函数序列不同分数算子μΙ对应的零极点指数的分布图如图7. 其中，横坐标ϖ表示零极点的频率指数，纵坐标表示不同的运算阶μΙ.

观察图7中不同阶数的零极点指数分布可知，当标度因子σ取值固定，阶数μΙ取值不同时，极点指数的值几乎不变，而零点指数之间的间距随阶数μΙ的增加而不断变大.

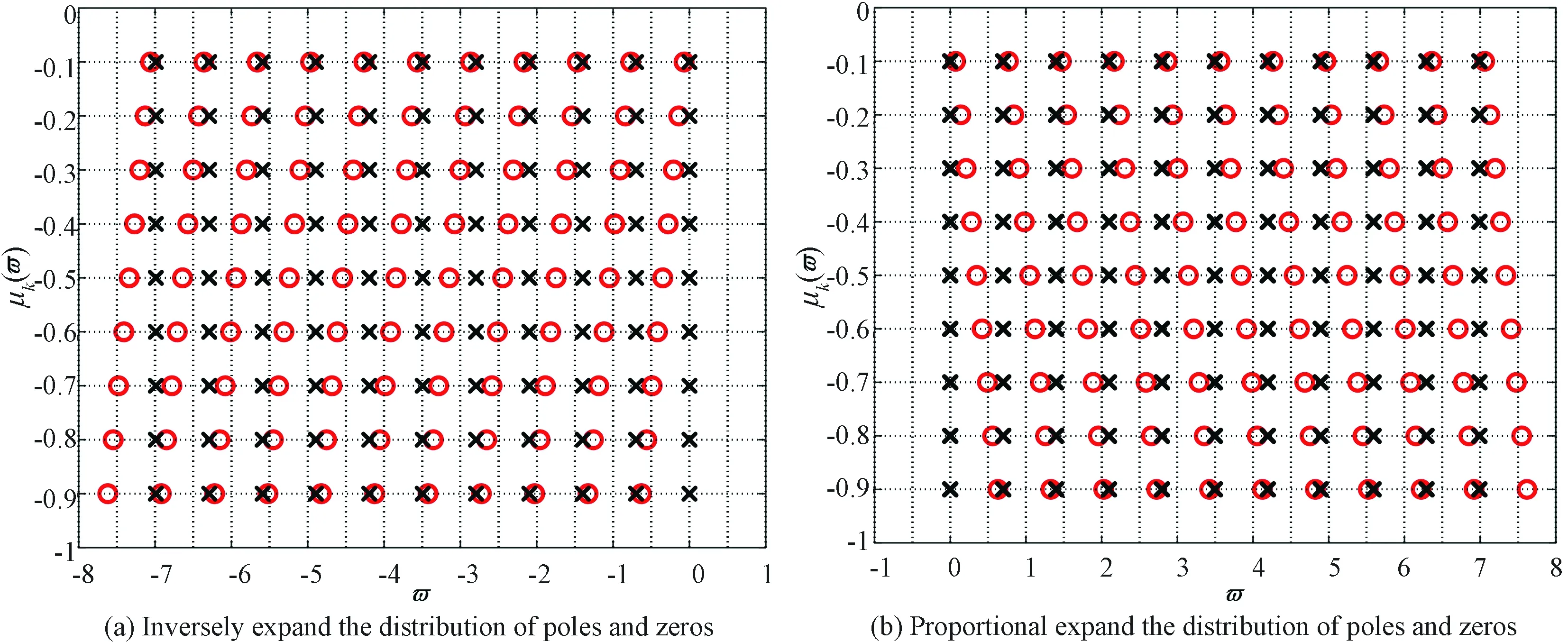
图7 正比和反比拓展时I型新颖标度方程不同阶数的零极点分布图(σ=5, σ=1/5, k=10)Fig.7 The distribution diagrams of poles and zeros of different orders of the I-type novel scaling equation with proportional and inverse expansion (σ=5, σ=1/5, k=10)

令阶数μΙ=-0.5，标度因子对数化lgσ分别取值为0.2、0.6、1.0、1.4，Ⅰ型新颖标度方程电路的节数k=15. 图8和图9分别是正比拓展和反比拓展在标度因子σ取值不同的频率指数分布. 根据施卜椿等[25]对标度分形分抗逼近电路的零极点分布规律的研究可知，零极点的值与节号i之间呈线性关系，此斜率与标度因子σ有关. 标度分形链与标度分形格电路等零极点的频率特征指数ϖk=-ilgσ.

观察图8和图9发现，不同的标度因子σ取值，零点频率指数与极点频率指数的斜率的确与lgσ相关.

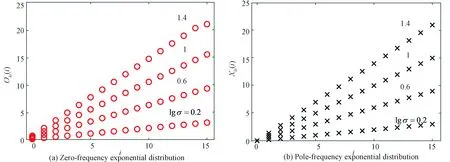
图8 I型新颖标度方程正比拓展不同标度因子σ零极点频率指数分布图(k=15)Fig.8 Type I novel scaling equation proportionally expands the exponential distribution diagram of zero-pole frequency with different scaling factors σ (k=15)

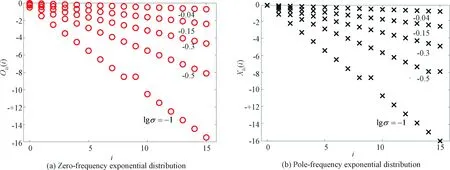
图9 I型新颖标度方程反比拓展不同标度因子σ零极点频率指数分布图(k=15)Fig.9 Type I novel scaling equation inversely expands the exponential distribution diagram of zero-pole frequency with different scaling factors σ (k=15)

根据仿真数据可得零极点线性分布规律的近似表达式如下式.

(31)

正比拓展或反比拓展的零极点分布都满足上式关系. 新颖标度方程取不同的σ值，其对应的零极点频率指数斜率为正标度因子的对数，与其他标度方程对应的斜率为负的标度因子的对数不相同，这是新颖标度方程的另一奇异性质的体现.

5 结 论

描述了分数算子的Charef有理逼近的具体逼近过程，用Z形逼近(递进分布的零极点对逼近)分形系统，将单分数幂极点传输函数重写成零极点对形式的有理函数. 单分数幂极点与幂零点系统的传输函数根据Charef有理逼近法以及零极点的分布关系，得到两个非正则的标度方程分别是Ⅰ型和D型新颖标度方程. 通过对新颖标度方程的运算性能的分析，近似求解发现Ⅰ型和D型新颖标度方程在高频范围内实现正或负任意阶分数算子wu有理逼近，在低频段都不具有分数阶特性. 发现这一有效频段不同以往典型的非正则标度方程的近似解结果，这是新颖标度方程的第一点奇异性质. 接着对新颖标度方程迭代生成的有理函数函数序列式(26c)求真实解，得到反比扩展的情况下在低频段具有运算有效性，这与近似求解的结论不符. 真实解与近似解的结果不符，这是新颖标度方程的第二点奇异性质. 进一步分析Charef 标度方程的零极点分布情况，发现在正比或反比拓展的情况下分别取不同标度因子的值，零极点频率指数分布的斜率为lgσ，这与其他典型标度方程的零极点指数斜率-lgσ不同，这是第三点奇异性质.

根据分数阶算子的Charef有理逼近过程获得的新颖标度方程，分析其奇异的性质只是研究的开端部分. 后续还有如下可以深入研究的内容以及问题善待解决：(1) 关于新颖标度方程反比拓展的近似解无法使用Liu氏粗解解释真实解的结果，本文目前无法解释该现象的原因，或许存在异于Liu氏粗解的关于非正则标度方程的新解法；(2) 通过阶频指标O、相频指标P和斜率指标K等，探寻新颖标度方程其他的奇异性质；(3) 根据新颖标度方程，给出一个具体的电路应用实例.