军航飞机流穿越民航航线冲突探测与解脱问题
吴明功, 蒋旭瑞, 温祥西,*, 陈彬
(1. 空军工程大学空管领航学院, 西安 710051;2. 国家空管防相撞技术重点实验室, 西安 710051;3. 中国人民解放军94116部队, 和田 848000; 4. 中国人民解放军军事科学院, 北京 100091)
近年来,随着民航运输量迅速增长,军航训练任务复杂繁重,军民航的防相撞工作越来越被人们关注[1]。通常情况下,民航飞机按照机场-终端区-航路航线飞行,军航飞机在各自训练空域内活动,军民航间空中交通安全压力不大;但在战斗机转场、重大演习任务、远程远海训练,甚至战时空域使用等特殊情况下,军航飞机穿越航路航线使飞行冲突的可能性大大增加,给空中交通安全带来了巨大压力。当前,航路航线上划设有固定穿越地带,当军航飞机流需要穿越航线时,军民航管制员需事先协调,在确保没有民航飞机使用时快速穿越。以上方式存在许多缺点:①多方人员协调,容易出错;②使用受限于固定穿越地带,灵活性差,与演习和战时高强度快节奏不相适应;③利用效率低,与空管安全高效的原则不符。为保证飞行安全,降低管制员工作负荷,寻找一种适用于以上场景的智能化冲突探测与解脱方法十分关键。
飞机流穿越航线飞行的冲突探测与解脱问题是一个复杂的系统工程,涉及到交通流理论、安全性评估和冲突探测与解脱技术等多领域交叉内容,本文主要针对这一场景展开建模分析,并提出了一种探测与解脱方法。在对飞机流的建模研究中,1981年, Hsu[2]提出了一种交叉航路飞机碰撞风险评估模型; Mao等[3-5]分析了汇聚飞机流采用平移解脱和航向解脱的稳定性,发现该方法鲁棒性较强,不产生多米诺效应,提出了紧凑配置的飞机流穿越方法;王莉莉和王坤[6]基于实际空管运行,从宏观和微观角度建立了纵向间隔的计算模型,提出了对航空器进行间隔调整的方案。其他以飞机流为研究对象的文献,从流量控制和容量评估角度研究得较多,对该飞行状态下的冲突探测与解脱问题研究得较少。韩松臣等[7]研究了交叉点两飞机之间标称距离随时间变化导致的碰撞风险,提出了一种航路交叉点处标称距离随时间变化的碰撞风险估计方法。在冲突解脱方法的研究中,主要有几何法、人工势场法、优化算法、控制论和博弈论等方法。博弈论方法因计算效率高、优化资源配置效果突出等优点被广泛采用。Tomlin等[8]使用非合作博弈论研究两机在最差航迹下保持安全间隔的初始状态;崔军辉等[9]使用微分对策理论对感知-规避问题给出了安全区域对无人机飞行策略和制导律的影响;朱衍波等[10]使用效益博弈解决双机飞行冲突,为博弈论在飞行冲突解脱中的应用提供了指导性思路;蒋旭瑞等[11]比较了航向机动下解脱方式与效益的关系,利用合作博弈方法计算解脱策略。
针对军航飞机流穿越民航飞机流模型特点,本文提出了一种基于滑动窗口的飞行冲突探测方法,对潜在冲突机进行分组。基于此,将存在冲突的飞机组考虑为一个联盟(coalition),提出了基于合作博弈的冲突解脱方法,通过调整飞机权重使民航飞机流以较小代价辅助避让,军航飞机以较大角度、较高速度机动避让。以航向-速度机动解脱边界条件为安全约束,以联盟福利最优解为解配置均衡各方效益,解算出避让策略。为满足解算的实时性要求,根据冲突区域不同的特点,利用免疫粒子群优化算法对搜索方向进行优化,加快收敛速度。希望通过以上工作,在保证飞行安全的前提下,提高军航飞机流穿越航线运行效率。
1 汇聚飞机流冲突探测模型
1.1 保护区模型
管制员一般通过比较两机间隔与安全间隔的大小判断冲突,而冲突探测与解脱问题中,应为飞机建立更加科学的保护区。目前,应用较为广泛的有E模型和V模型[12],本文采用椭球E模型。由于只考虑同高度层内的冲突问题,故保护区简化为半径为a的圆,如图1所示。
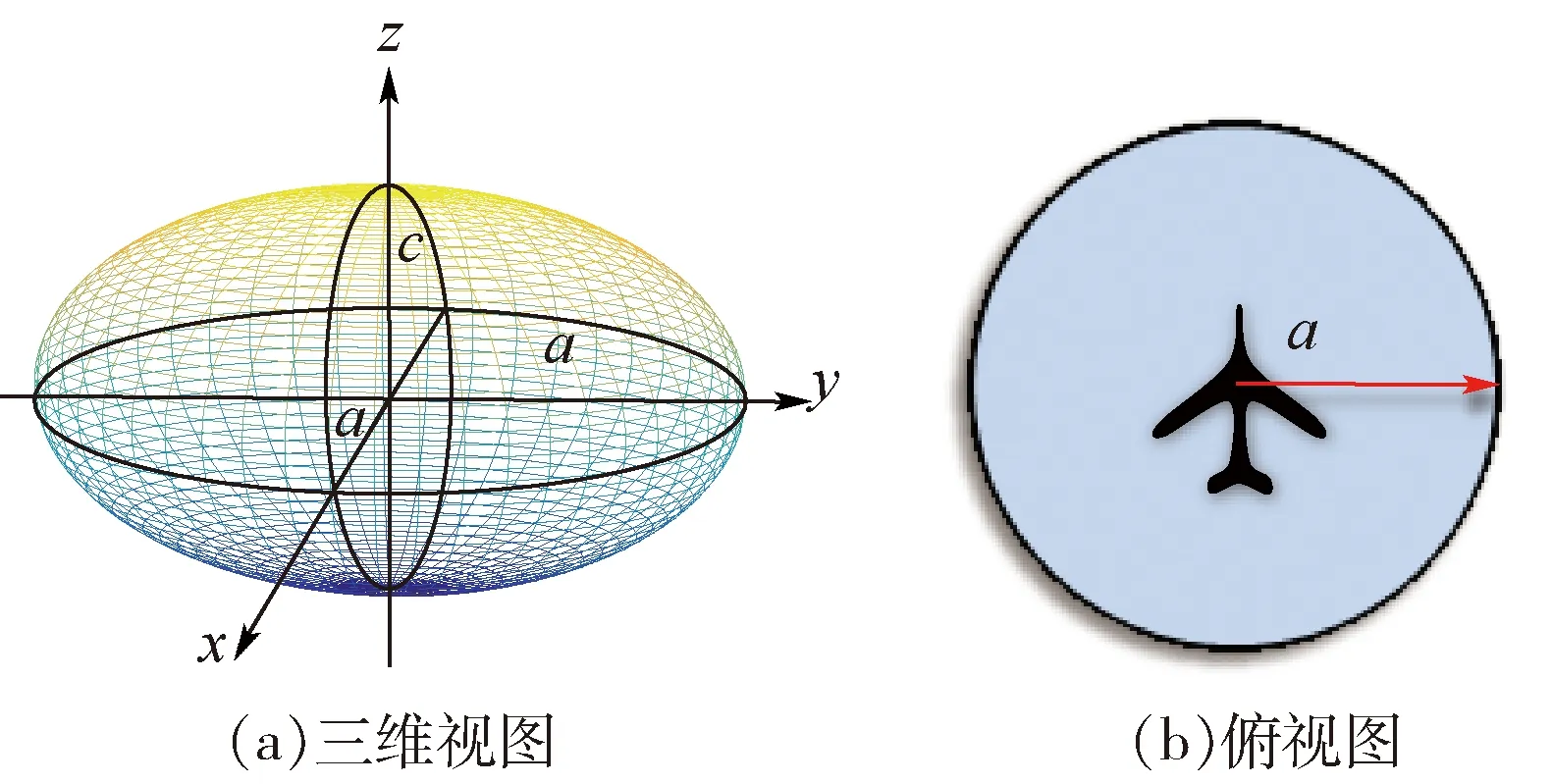
图1 保护区E模型Fig.1 E model of safe separation zone
根据安全间隔标准,取保护区半径a=2.5 n mile。若两机保护区重叠,则存在飞行冲突。
1.2 滑动窗口探测模型
军航飞机流按直线编队飞行,民航飞机流在宽度为L′=20 km的航路内飞行。在任意需穿越的航线上划设汇聚控制区,飞机流进入控制区后,军航飞机沿保护区投影出一条宽度为a(与保护区半径相等)的矩形滑动窗口(见图2中矩形阴影区域),并随飞机移动(平移),若探测窗口与民航飞机保护区重叠,则表示两机到达汇聚点时存在潜在冲突。军航飞机通过改航和调速进行冲突解脱,此时,滑动窗口也随飞机移动(旋转)。冲突探测场景可由图2表示。
为便于观察,图2中将飞机放大表示,且进入控制区后不进行机动。特别地,当两飞机流速度相等时,滑动窗口与水平方向夹角为45°。汇聚控制区半径R由保护区半径、飞机流速度以及飞机机动性能等共同决定。根据以上分析,可以得出以上各机之间的潜在冲突关系如图3所示。可以看出,各飞机流内部之间不存在预先冲突,军民航飞机流间冲突可以表现为单对单、多对单、单对多和多对多等多种形式。
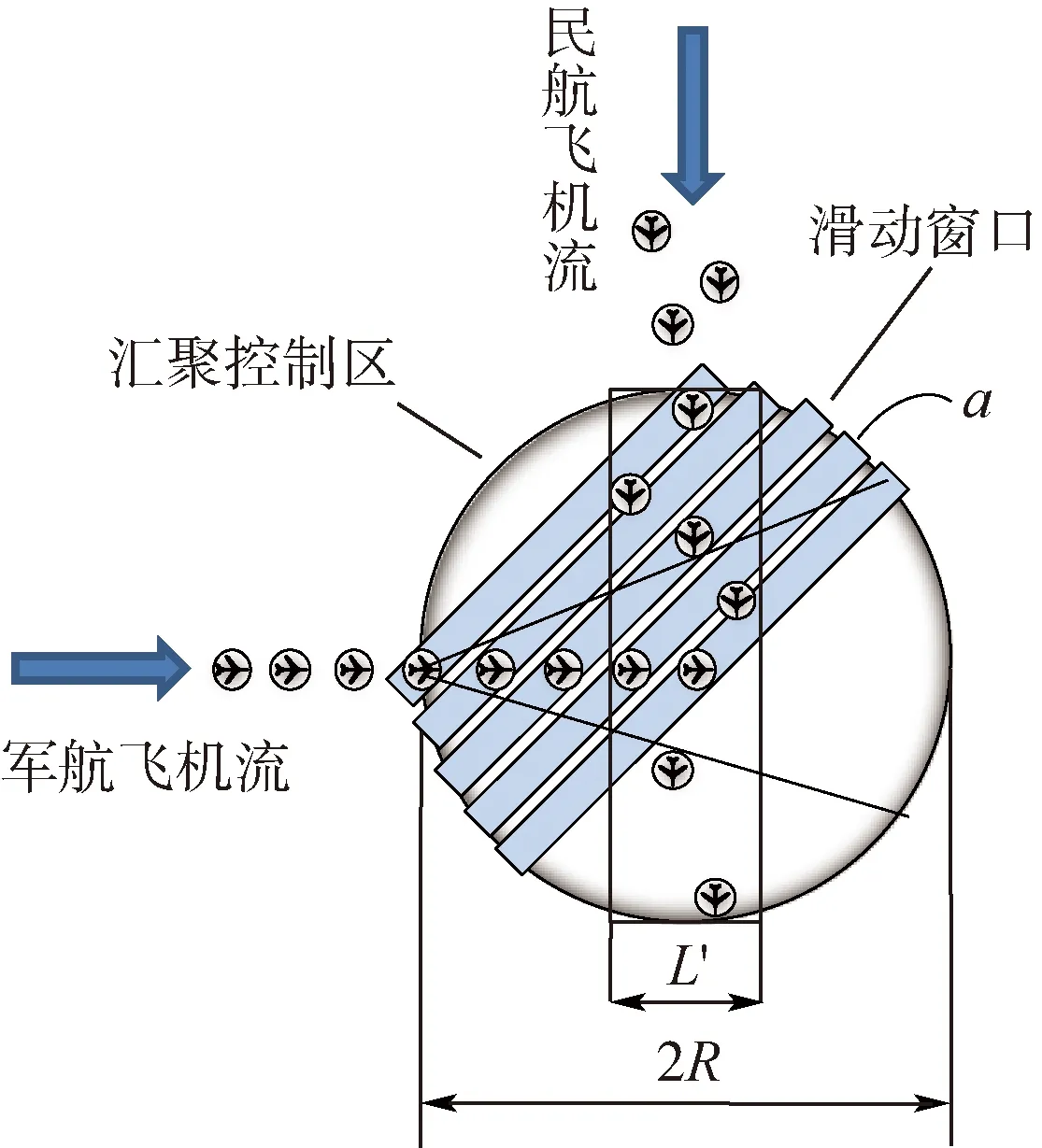
图2 冲突探测场景Fig.2 Conflict detection scenario
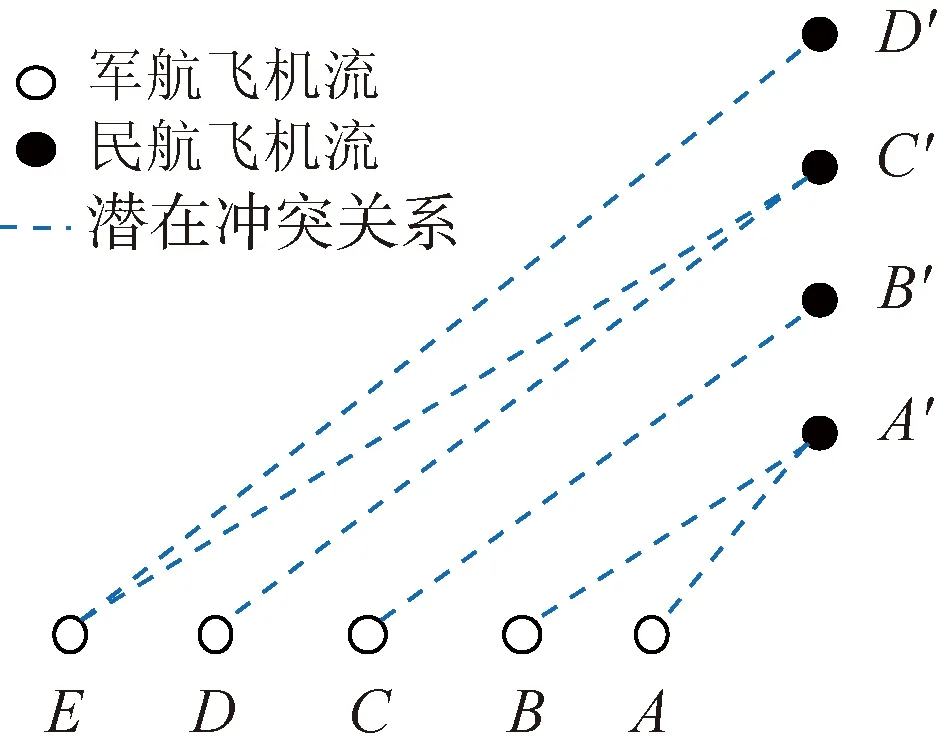
图3 飞机流之间各机冲突关系Fig.3 Conflict relationship within aircraft flows
1.3 冲突区域分析
从图2可以发现,飞机冲突时两机位置关系可以分为图4所示的2种情况。
尽管2种情况下两机均存在冲突,但两机位置稍有差异。图4(a)中,两飞机保护区投影右侧边界穿过对方保护区,存在右侧冲突,若沿虚线箭头方向(最优机动方向)向左机动,可快速解脱;图4(b)中,两飞机保护区投影左侧边界穿过对方保护区,存在左侧冲突,若沿虚线箭头方向向右机动,可快速解脱。
若飞机两侧均存在冲突,则需考察两侧飞机到滑动窗口长边的最长距离。
(1)
式中:dLmax≥di对于∀di∈DL都成立;dLmax≥dj对于∀dj∈DR都成立;Dmax为最优机动方向,1对应左转,-1对应右转,0对应不转;dLmax为左侧冲突的飞机集合中,到滑动窗口长边的最长距离;dRmax为右侧冲突的飞机集合中,到滑动窗口长边的最长距离。以最优机动方向解脱,飞机支付的代价最小。
最优机动方向的确定将为第3节中粒子群优化算法引入免疫机制提供指导思路。
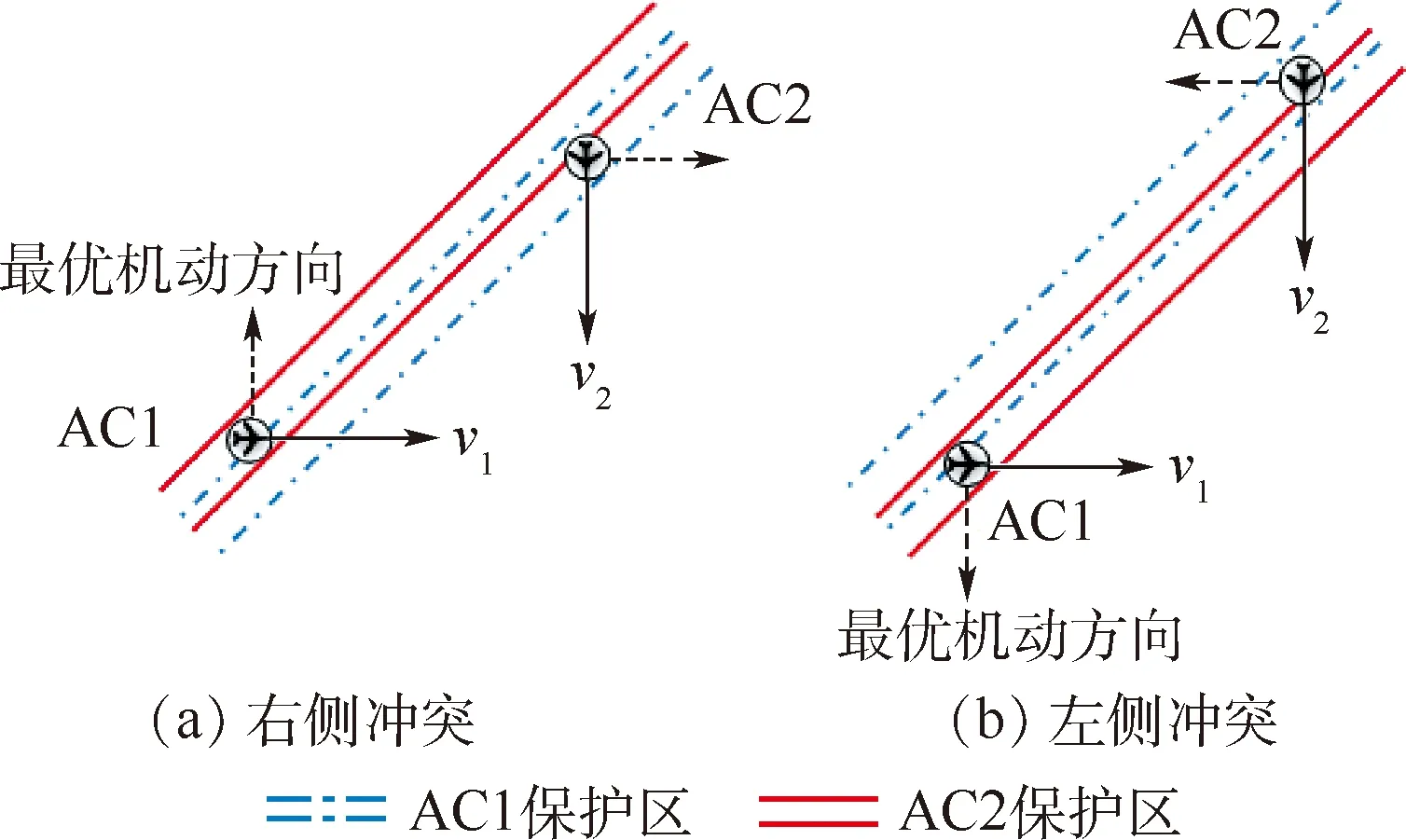
图4 两机冲突位置关系Fig.4 Position relationship between two conflicting aircraft
2 基于合作博弈的冲突解脱策略
2.1 合作博弈解的概念
合作博弈是指在协议的约束下各方利益都有所增加,或者在不损害任意一方利益的前提下,有参与者利益增加,从而整个联盟的利益有所增加。与非合作博弈相比,合作博弈更加强调集体主义和团体理性(collective rationality),主要研究了参与者达成合作时如何分配合作所得收益的问题。联盟内部的信息互通和存在有约束力的可执行契约是达成合作博弈的2个前提条件。
合作博弈在发展的过程中提出了众多的解概念,其基本思想就是要设计出一种公平解(fair allocation),促使参与者在不损害联盟利益的前提下获得更高的收益。以联盟福利最优解[13-14]为解配置均衡各方利益,联盟福利最优解要满足以下3个条件:
1) 联盟参与人具有为联盟整体谋求最大福利的行为。
2) 联盟参与人具有追求公平的偏好。
3) 联盟参与人追求个人利益和公平性不能以牺牲联盟福利为代价。
2.2 合作博弈冲突解脱模型
通过探测模型发现的潜在冲突飞机组构成一个联盟,联盟中各局中人I={i|i∈[1,N]}的所有解脱策略组成策略空间Yi(yij∈Yi表示参与者i的第j个策略),在安全间隔的约束下互相博弈,并支付相应代价u={u1,u2,…,un}。支付函数ui:Y→R,表示第i位参与者在不同策略组合下解脱行为需要支付的代价。由每个参与者的某一策略构成的策略组合{y1,y2,…,yn}对应支付{u1,u2,…,un}加权求和,得到联盟福利函数为
(2)
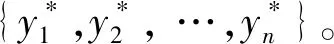
模型研究的主要对象是可能发生危险冲突的航空器联盟。参与者之间通过联盟获取更高的效用,而对于某个体航空器而言,其所选择的策略不一定是收益最高的,特别是在调整飞机权重系数ki后,军航飞机的解脱代价一定高于民航飞机。以联盟福利最优解为解配置,在保证航空器联盟安全的前提下,根据付出的总避让代价最小原则,确定出需要避让的飞机及其机动策略。
2.3 解脱策略与支付函数
因穿越高度层使问题更加复杂化,本文中选择航向-速度机动结合的方式。
1) 航向机动。规定民航飞机不作航向机动;军航飞机航向角改变范围为[-20°,20°],把航向角变化范围离散成相差5°的策略集合,共9种策略。
2) 速度机动。规定军民航飞机可加/减速10%、20%和30%,共7种策略。
机动后,若民航飞机脱离新的滑动窗口,则判定解脱成功。军民航飞机保持当前飞行姿态通过冲突区域,之后军航飞机按规定集合,民航飞机恢复航线飞行。
支付函数是参与者从博弈中获得的效用水平,表示避让支付的代价。支付代价取决于转角、速度改变量和解脱时间。该模型中,支付函数表示为
(3)
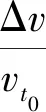
2.4 冲突解脱边界条件约束
飞机在解脱中支付越少机动成本将获得越高的效用,选择不避让的航空器将获得最高的收益。因此,为保证飞行安全,需设置约束条件,剔除掉策略组合中的不可行解。借鉴文献[3]中航向机动解脱判断方法,引入两机不同时到达的情况,推广到航向-速度机动的解脱边界条件判定中。模型示意如图5所示。
初始时刻t0,AC1和AC2分别位于初始位置S1和S2,速度分别为v和kv,AC2落后距离l,保护区半径为a,两机存在左侧冲突,解脱策略选择向右机动。解脱成功的充分条件可由以下推导得出。
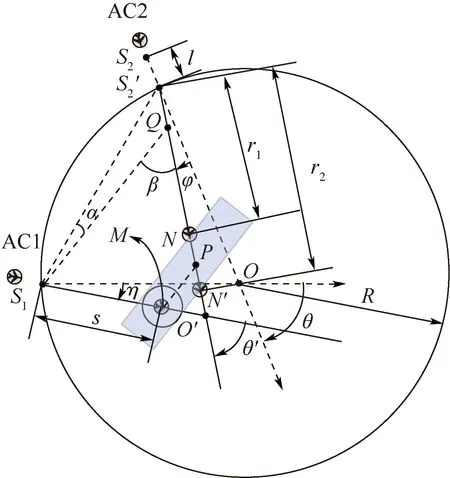
图5 两机冲突边界条件Fig.5 Conflict boundary condition of two aircraft
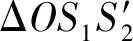
进入控制区后,两机右转解脱,转角分别为η和φ,交汇点从O变为O′,航向交叉角由θ变为θ′。
θ′=θ+φ-η
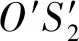
令d(O′,S1)=x,则d(O′,Q)=kx,上式可化为
sinβ=sinβcosθ′+cosβsinθ′
左右同除sinβ,得
又因P为N、N′中点,则
此时,AC2位于滑动窗口边缘位置恰好解脱。
(4)
或
(5)
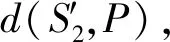
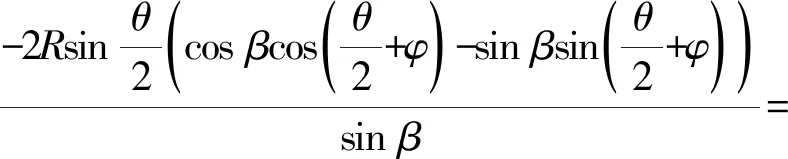
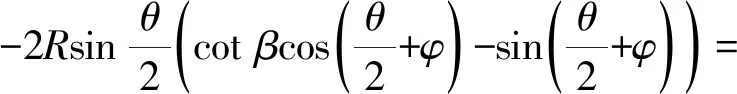
由于d(S1,M)=s,则d(Q,P)=ks。
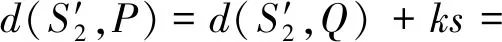
(6)
将式(6)代入式(4)、式(5),得到解脱的临界条件为
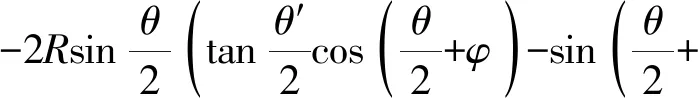
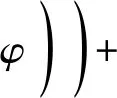
综上,在AC1前进距离s的情况下,只要AC2前进距离s′
3 基于免疫粒子群优化算法的冲突求解
在合作博弈冲突解脱模型中,遍历所有策略组合耗时过长,难以满足实时解算要求,这在工程实践中意义重大。为了解决这一问题,针对冲突区域不同的特点,把免疫机制引入粒子群优化算法。
粒子群优化算法是进化算法中一种用于优化的并行算法。初始化一群数量为N的随机粒子,在D维空间中通过重复迭代、更新自身的位置以搜索适应度值最优解[15]。在免疫机制生效过程中,机体针对不同抗原分别生成匹配抗体,抗体自动识别匹配抗原发挥免疫作用,同时若再遭遇此类抗原入侵,机体将快速进行免疫应答[16-17]。本节模拟免疫过程,在初始种群中注入抗原产生抗体,优化粒子搜索方向,提高算法收敛速度。整个免疫机理作用过程如图6所示。
在免疫作用过程中,抗原的选择直接影响算法求解速度,注入的抗原与目标解越相似,算法收敛越快。将1.3节中满足最优机动方向的策略集合作为抗原。算法的关键步骤如下:
1) 适应度函数
将联盟福利函数的倒数作为该问题的适应度函数,即
式中:k为某联盟中飞机架数。
2) 编码解码方式
按照表1所示方式编码与解码。表1中,Δv为速度改变策略,Δθ为航向角机动策略,策略pij=p(i,j)表示码表中i行j列的元素。
3) 免疫抗原注入
根据如下最优机动方向,为初始粒子群注入免疫抗原:
4) 约束条件
通过取整函数保证运算每一步粒子位置值均为整数。通过不断选择、改变超出边界的位置值保证解的可行性[18]。若粒子位置超出边界,将其置于边界位置,并将速度取反。
pij=10i+j
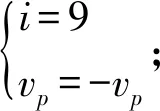
综上所述,针对军航飞机穿越民航航线问题的冲突探测与解脱方法设计可由图7表示。
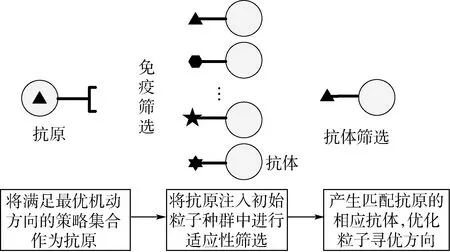
图6 免疫机理示意图Fig.6 Schematic of immune mechanism
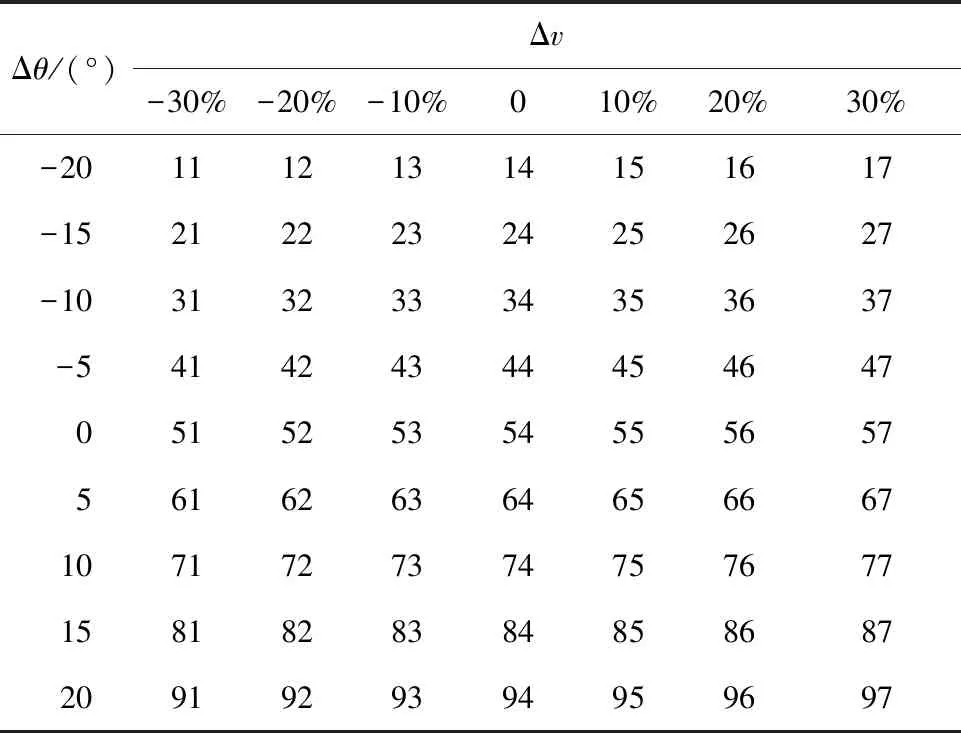
Δθ/(°)Δv-30%-20%-10%010%20%30%-2011121314151617-1521222324252627-1031323334353637-541424344454647051525354555657561626364656667107172737475767715818283848586872091929394959697
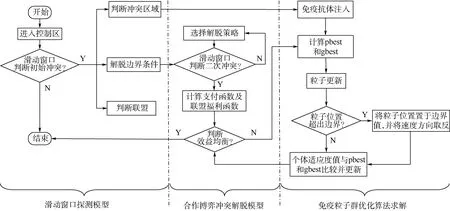
图7 冲突探测与解脱方法设计Fig.7 Conflict detection and resolution method design
4 仿真分析
民航飞机流数据由Flightware软件获取,某日23时15分A461航线某段航班信息如图8所示。
选取该段某高度层飞机流为民航飞机流初始位置,初始速度设置为700 km/h。控制区半径取R=50 km,保护区半径a=2.5 n mile,航路宽度L′=20 km。以MATLAB平台仿真产生1批7架军航飞机,以纵向间隔d=15 km沿直线编队飞行,初始速度大小按照规定调整为与民航飞机相同。设置军民航飞机权重系数分别为k1=1,k2=2;飞行角度改变权重系数w1=9,飞行速度改变权重系数w2=25。初始状态如图9所示。
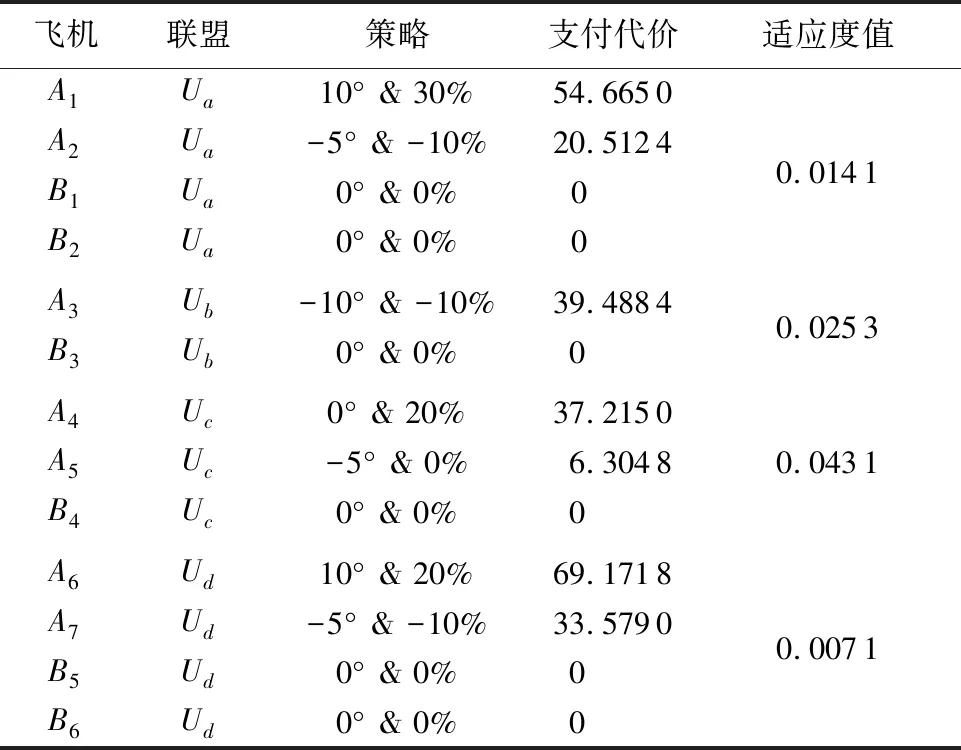
初始t0时刻,各机均满足安全状态。因初始速度大小相等,由倾斜角γ=45°的滑动窗口探测可知,联盟Ua由飞机A1、A2、B1、B2构成;联盟Ub由飞机A3、B3构成;联盟Uc由飞机A4、A5、B4构成;联盟Ud由飞机A6、A7、B5、B6构成。联盟内部各局中人围绕支付代价展开博弈。通过改进粒子群优化算法解算出的最优策略见表2。
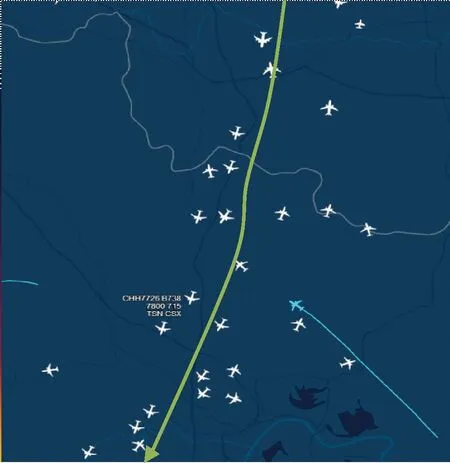
图8 民航飞机流信息获取Fig.8 Civil aircraft flow data acquisition
从表2可以看出,民航飞机流均不需机动;军航飞机中没有需要转向10°以上的策略,仅有1架飞机需加速30%,总体来说解脱支付代价较少。其航迹如图10所示。
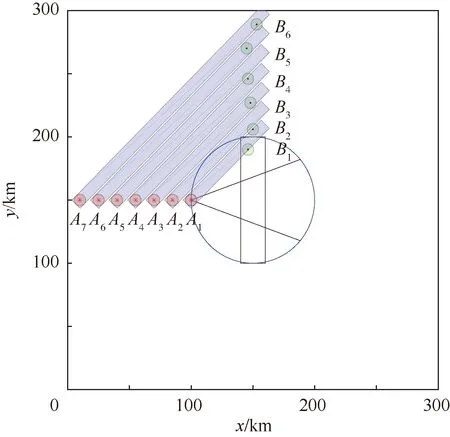
图9 初始状态Fig.9 Initial state
飞机联盟策略支付代价适应度值A1Ua10° & 30%54.6650A2Ua-5° & -10%20.51240.0141B1Ua0° & 0%0 B2Ua0° & 0%0 A3Ub-10° & -10%39.4884B3Ub0° & 0%00.0253A4Uc0° & 20%37.2150A5Uc-5° & 0%6.3048B4Uc0° & 0%00.0431A6Ud10° & 20%69.1718A7Ud-5° & -10%33.5790B5Ud0° & 0%0B6Ud0° & 0%00.0071
为了便于观察,将t=300,400,500,600 s时刻的空中飞机状态用快照形式展示,分别观察分析联盟Ua、Ub、Uc、Ud的避让策略,可以总结出启示性结论,如图11所示。
图11中,圆形、锥形和矩形分别为控制区(CZ)、机动区(MZ)和航路(AR)。图11(a)中,飞机A1与飞机B1存在右侧冲突,与B2存在左侧冲突,根据式(1)可知,右转为最优机动方向,飞机A1右转10°并加速30%快速规避冲突;飞机A2与飞机B2存在右侧冲突,左侧为最优机动方向,飞机A2左转5°并减速10%。图11(b)中,飞机A3与飞机B3恰好同时到达冲突点,在安全约束下,民航机B3不机动,军航机A3左转10°并减速10%恰能避免冲突。图11(c)中,A4与A5分别与B4存在左侧冲突和右侧冲突,最优解脱方向应分别是右转和左转,解算出的解脱策略为A4加速20%,A5左转5°,B4不机动。图11(d)中,A6与B5、B6存在潜在冲突,根据式(1)求解出最优解脱方向为右转;A7与B6存在右侧冲突。解算出的解脱策略为A6右转10°并加速20%,A7左转5°并减速10%,B5、B6保持原飞行状态。可以发现,联盟内部军民航冲突机之间加减速策略相反;军航飞机若需大尺度机动,左转与减速,右转与加速一般是同时执行的;该场景中所有民航飞机未机动。与管制运行中的规律相吻合,并达到了预期目的,验证了该方法的科学性。
在解脱过程中,每架飞机支付代价如图12所示。
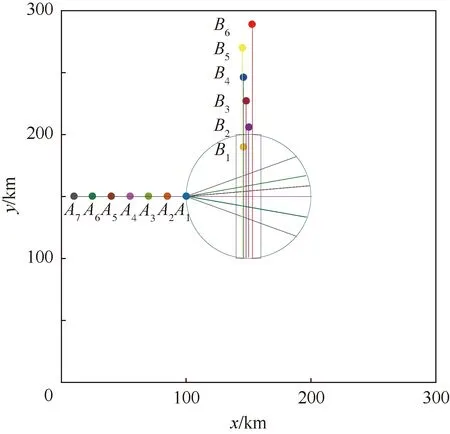
图10 飞机流汇聚飞行解脱航迹Fig.10 Resolution track of centering aircraft flow
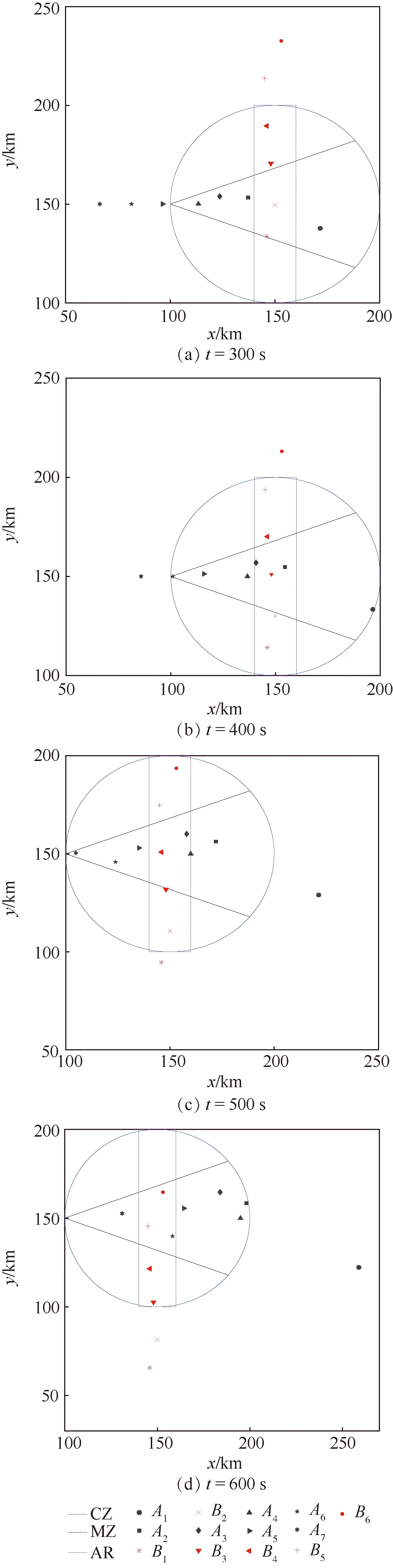
图11 飞行状态快照Fig.11 Flight status snapshot
图12中,民航飞机因未机动避让,支付代价均为零。从理论上而言,军航飞机中机动角度越大、速度变化量越大,支付代价应越高。A1增速虽然大于A6,但支付却更少。这是因为A1以较大速度脱离控制区,满足了联盟对于安全性的要求,进一步说明了支付函数的合理性。考察算法的收敛性,观察策略的适应度值随收敛代数的变化情况,结果如图13所示。
从图13中可以看出,免疫粒子群优化算法具有跳出局部最优的能力,并在40代后收敛,运算时间为3.36 s,满足实时性的要求。粒子群优化算法中适应度值随收敛代数变化情况如图14所示。
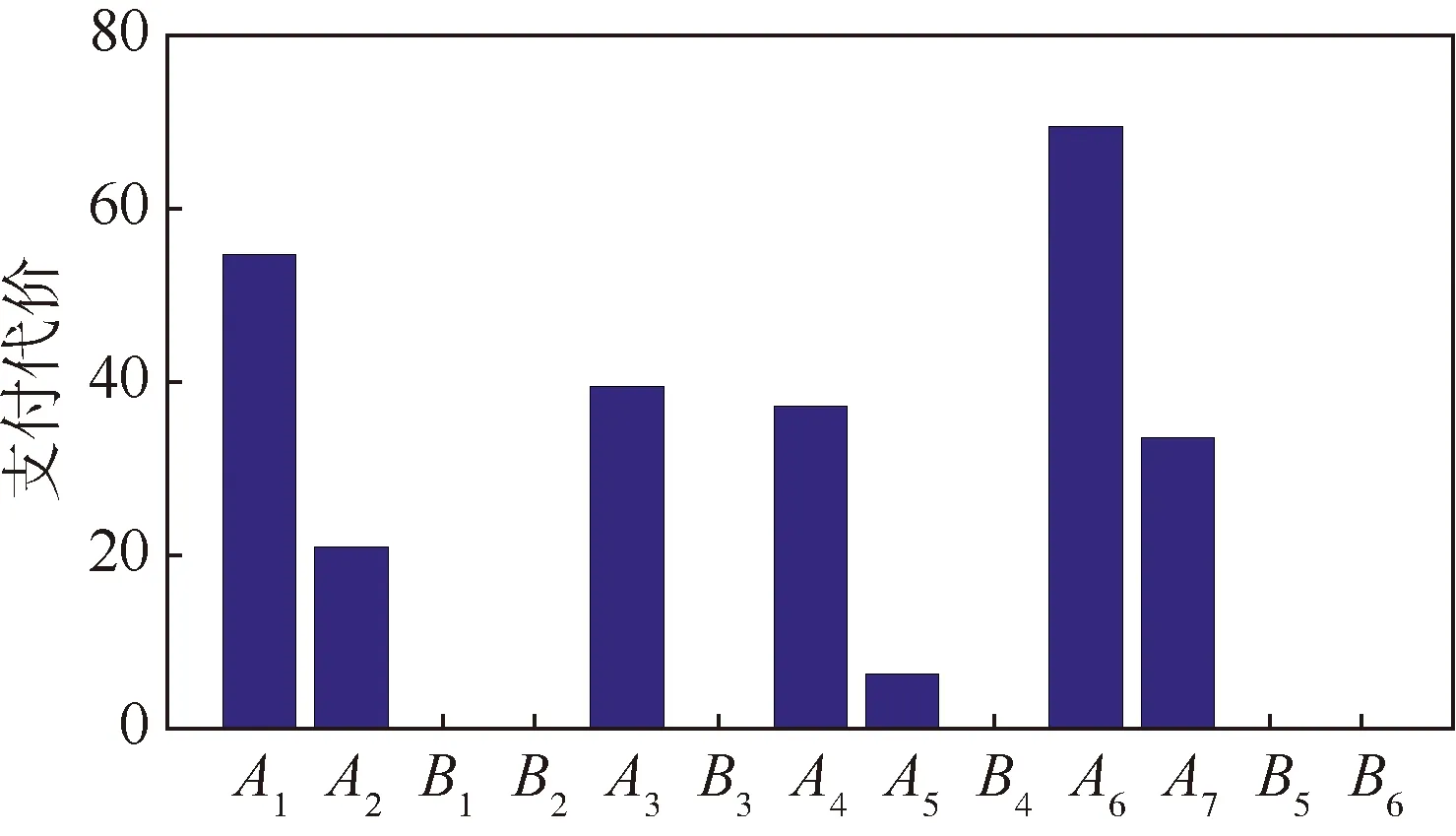
图12 各飞机解脱支付代价Fig.12 Resolution pay-off of each aircraft
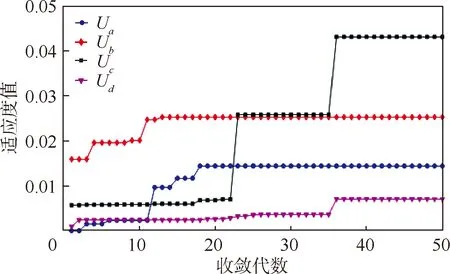
图13 免疫粒子群优化算法适应度值随收敛代数的变化Fig.13 Fitness value of immune particle swarm optimization algorithm changes with convergence algebra
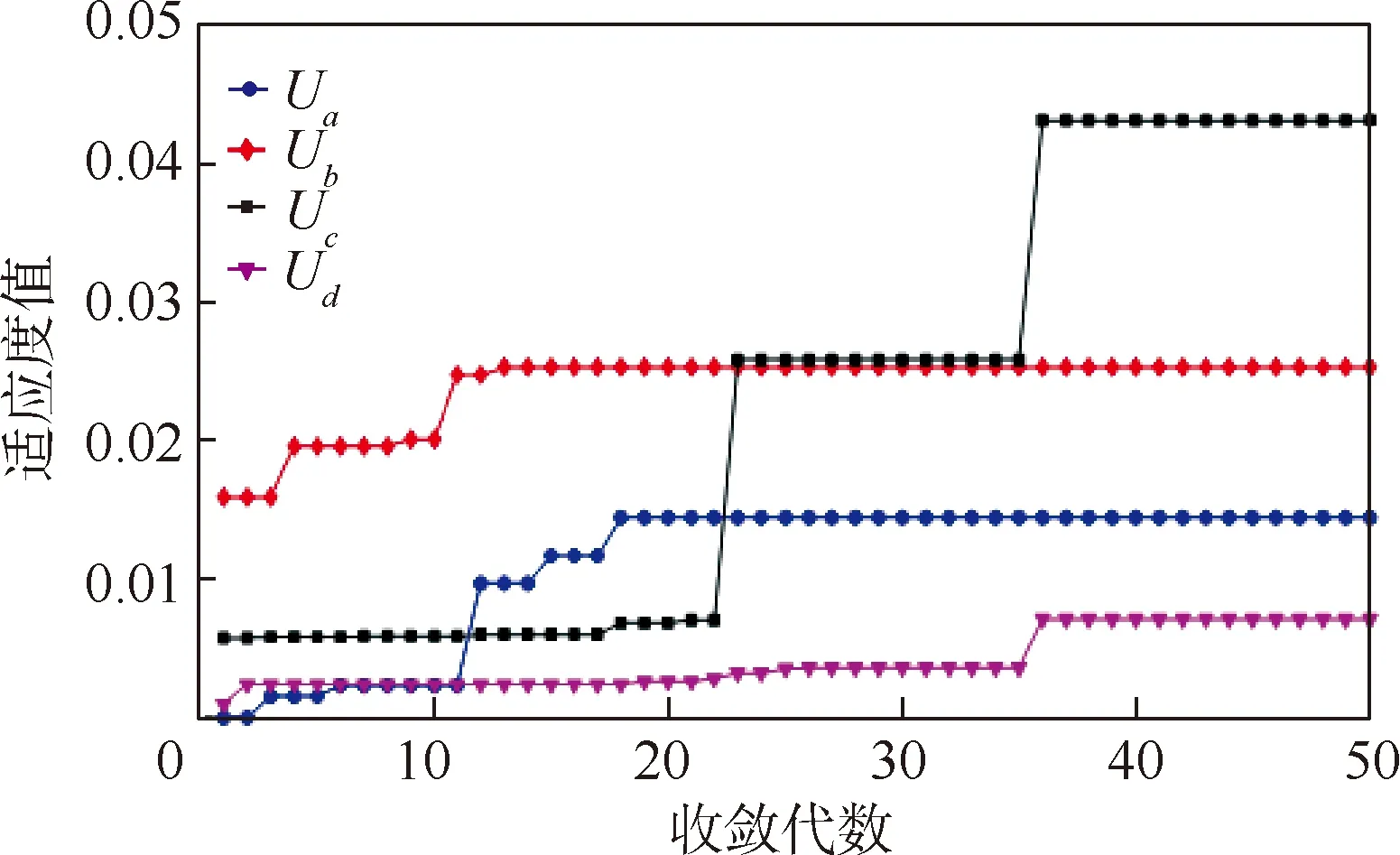
图14 粒子群优化算法适应度值随收敛代数的变化Fig.14 Fitness value of particle swarm optimization algorithm changes with convergence algebra
粒子群优化算法运行时间为12.87 s。对比图13与图14可知,免疫粒子群优化算法跳出局部最优的能力更强,且收敛于更高的效用水平。
5 结 论
1) 本文对飞机流穿越民航航路问题进行了建模分析,提出了基于滑动窗口的探测模型,提炼出飞机联盟、解脱边界条件与最优机动方向。
2) 提出的合作博弈冲突解脱模型能在保证安全间隔的前提下较好地均衡各飞机收益,通过增加民航飞机权重使客机尽量少机动避让。
3) 将存在潜在冲突的飞机划分联盟,进行分布式地解脱,可有效降低算法复杂度,缩短了解算时间;免疫粒子群优化算法能快速计算出满足安全间隔要求的冲突策略。
在下一步工作中,将分析飞机流汇聚角度、飞机初始间隔和控制区域大小对于解脱效果的影响,总结出军航飞机穿越航线飞行的一般规则。

