高空太阳能无人机三维航迹优化

王少奇， 马东立， 杨穆清， 张良

(北京航空航天大学航空科学与工程学院, 北京 100083)

近年来，能源危机和环境污染已经成为人类社会面临的主要挑战。太阳能无人机依靠铺设在机翼表面的太阳能电池将太阳辐射能转化为电能，通过电机驱动螺旋桨产生前进动力，具有可持续、无污染的特点。高空太阳能无人机能够在平流层飞行数天乃至数月，可以广泛应用于遥感、侦察、通信等诸多领域，成为近年来各国研究的热点[1-3]。

目前，太阳能无人机昼夜闭环飞行高度和载荷能力的进一步提升主要受太阳能电池效率和储能电池能量密度等因素的制约[4]。这些子系统技术水平的提升需要投入大量时间和经济成本。而由于能源系统的特殊性，飞行航迹优化为提升高空太阳能无人机飞行性能和载荷能力提供了一个重要途径，应当引起足够的重视[5]。

国内外针对太阳能无人机飞行航迹优化的措施主要集中在2个方面。一是通过改变无人机飞行姿态，增加净吸收能量。Klesh和Kabamba[6-7]利用极大值原理给出了水平面内点到点飞行任务最优航迹的解析解。Spangelo和Gilbert[8-9]采用周期性样条函数来表示航迹，研究了短时间小半径盘旋时的最优航迹。Ma等[10]推导了最优转弯过程的必要条件，并进一步得到了转弯过程中的最优滚转角控制率。Dai[11]考虑了天气因素，结合图谱法和Bellman-Ford搜索算法，研究了低空水平飞行的航迹规划问题。在此基础上，Vasisht、Mesbahi[12]和Wu等[13-14]针对地面目标追踪、多机联合监视等特殊任务开展了航迹优化。在这些研究中，无人机的运动限定在二维水平面内。另一个措施是通过改变飞行高度，利用重力储能代替部分储能电池的作用。Gao等[15-17]采用高斯伪谱法研究了下滑过程的最优航迹，分析了重力储能和二次电池的等价性，并提出了一种昼夜闭环能量管理策略。Xu等[18]基于锂电池的充放电特性，提出了相似的飞行策略。在这些研究中，无人机的运动限定在二维铅垂平面内。目前国内外学者针对太阳能无人机航迹优化的研究已经取得了很大进展。但同时采取上述2种措施对高空太阳能无人机在三维运动时的航迹优化研究还鲜见相关文献资料。

本文建立了高空太阳能无人机三维航迹优化模型，研究同时利用改变飞行姿态和飞行高度2种措施来提升飞行性能的效果。采用高斯伪谱法离散状态方程和约束方程，将最优控制问题转化为非线性规划问题。针对典型的点到点飞行任务，以储能电池剩余电量为目标函数，优化得到了能量最优飞行航迹，并与常规定高定速航迹进行了对比分析。

1 航迹优化建模

1.1 动力学模型

假设无人机具有纵向对称平面，如图1所示。无风条件下的质点动力学方程为

(1)

式中：x、y、z为地面坐标系下的无人机位置坐标；V为空速；γ为爬升角；χ为航迹偏角；φ为滚转角；m为无人机质量；g为重力加速度；L、D和T分别为升力、阻力和螺旋桨推力。阻力和螺旋桨推力平行于速度方向，升力垂直于速度方向。地面坐标系Og-XgYgZg和机体坐标系Ob-XbYbZb的定义如图1所示。

升力L和阻力D可以表示为

(2)

式中：ρ为空气密度；S为机翼面积；CL和CD分别为升力系数和阻力系数。

图1 地面坐标系和机体坐标系示意图Fig.1 Schematic diagram of earth-fixed coordinate system and aircraft body-fixed coordinate system

CL、CD受翼型、迎角α和雷诺数Re的影响，通过式(3)计算，式中系数Aij、Bij通过计算流体力学(Computational Fluid Dynamics，CFD)方法得到，数值见表1和表2。

(3)

飞行高度越高，侦察范围越广，对z坐标作如下限制。

z≥Hmin

(4)

式中：Hmin为执行任务所允许的最低飞行高度，取15 km。

表1 系数Aij的值Table 1 Value of coefficients Aij

表2 系数Bij的值

1.2 能源系统模型

1.2.1 太阳能电池模型

对于高空太阳能无人机，因其大部分时间飞行在云层之上，可以忽略云层的遮挡。太阳能电池输出电功率Psc为

Psc=PsdSscηscηMPPTcosκ

(5)

式中：Psd为太阳光谱密度；Ssc为太阳能电池面积；ηsc为太阳能电池效率；ηMPPT为最大功率点跟踪(Maximum Power Point Tracking，MPPT)控制器效率；κ为太阳入射角。

太阳入射角κ可以表示为

(6)

太阳能电池板单位法向量在地面坐标系中可表示为

(7)

入射光线单位向量在地面坐标系中可表示为

(8)

式中：αe和αa分别为太阳高度角和方位角，可通过式(9)确定。

(9)

式中：Φ为当地纬度；δ为太阳赤纬；ωt为太阳时角；nd为一年中的日子数(从1月1日开始计)；th为真太阳时。

1.2.2 储能电池模型

锂硫(Li-S)电池能量密度较高，具有作为太阳能无人机二次电源的应用前景[19]，其充电速率可以表示为[20]

(10)

式中：VOC为开路电压；RI为电池内阻；QB为电池容量；PB为电池放电功率；SOC表示储能电池的电量状态，定义为当前电量与最大电量的比值。

为使Li-S电池具有更长的循环寿命，将SOC的值限制在如下范围：

0.25≤SOC≤0.9

(11)

1.2.3 功率消耗模型

太阳能无人机的功率消耗部件包括电机和机载电子设备，其中机载电子设备的功率相对较小，在本文中忽略。电机提取功率为

(12)

式中：ηm为电机效率；ηp为螺旋桨效率。ηp受螺旋桨前进比λ和特征雷诺数Rep的影响，通过式(13)计算。

(13)

式中：系数Cij由CFD方法得到，数值见表3，λ和Rep的定义分别如式(14)和式(15)所示。

表3 系数Cij的值Table 3 Value of coefficients Cij

(14)

(15)

式中：Dp为螺旋桨直径；n为转速；c0.75R为桨叶75%半径处的当地弦长；μ为空气动力黏性系数。

电机提取功率需满足：

Pm-Psc-PB≤0

(16)

1.3 优化问题描述

以α、φ、PB、T为控制变量，以任务结束时刻储能电池的电量状态SOCf为目标函数，高空太阳能无人机三维飞行航迹优化问题可以描述为最优控制问题，即

(17)

并满足式(1)、式(10)组成的状态方程，同时满足式(4)、式(11)和式(16)组成的过程约束条件。

2 离散方法

第1节中的最优控制问题的时间区间定义在[t0,tf]，经式(18)变换到[-1,1]。

(18)

以N阶Legendre-Gauss多项式GN(τ)的零点τ={τ1,τ2,…,τN}作为配点，τ分布在区间(-1, 1)上，添加τ0=-1，以τ*={τ0,τ1,…,τN}作为离散点。

(19)

以N+1阶Lagrange插值多项式Li(τ)作为基函数，将状态变量近似为

(20)

式中：

(21)

类似地，将控制变量近似为

(22)

式中：

(23)

将状态变量的时间导数近似为

(24)

式中:k=1, 2, …,N。

初始时刻状态变量满足：

X(-1)=x0

(25)

结束时刻状态变量X(1)采用高斯积分估计：

X(1)=X(-1)+

(26)

式中：Ak为高斯积分系数，可表示为

(27)

通过采用高斯伪谱法，将最优控制问题转化成为非线性规划问题，待优化参数为：x(τi),i=0,1,…,N和u(τi),i=1,2,…,N。

3 优化结果分析

3.1 仿真参数

高空太阳能无人机参数见表4，各部件的能量转换效率见表5。考虑一种典型的点到点飞行任务，即从指定的初始点出发，在给定的时间到达指定的终点。假设无人机在北京(39.9°N)上空飞行，日期为3月21日，太阳光谱密度为1 352 W/m2。初始时刻为0 h，初始时刻无人机位置坐标为[0 0 0]Tm，储能电池电量状态SOC0=0.6；结束时刻为24 h，结束时刻无人机位置坐标为[0 0 0]Tm。

表4 高空太阳能无人机基本参数Table 4 Basic parameters of high-altitude solar-powered UAV

表5 各部件能量转换效率

3.2 结果分析

作为对比，首先给出一种常规飞行航迹。在这种航迹中，无人机以有利速度在任务允许的最低高度定高定速飞行。其能量管理策略为：

1) 当Psc=0且SOC>0.25时，令PB=Pm。

2) 当Psc>0且0.25≤SOC<0.9时，令PB=Pm-Psc。

3) 当Psc>0且SOC=0.9时，令PB=0。

取配点数量N为50，优化得到能量最优航迹，与常规航迹的仿真结果对比见表6。与常规航迹相比，优化航迹能使储能电池剩余电量提高18.8%，相当于可以使储能电池重量减小6.5 kg。这些重量可以省掉，也可以分配给任务载荷，将使得飞行性能进一步提高。此外，结果显示SOCf>SOC0，这意味着无人机可以在储能电池剩余电量不减小的前提下完成下一个昼夜循环，使数天乃至数月的超长航时飞行成为可能。

图2给出了常规航迹和优化航迹对应的太阳能电池输出电功率Psc、储能电池放电功率PB及电机提取功率Pm曲线。根据优化航迹的特点，将其分为4个阶段。在常规飞行航迹中，Psc的最大值为4 189 W，出现在t=12 h。而在优化航迹中，通过改变飞行姿态，Psc得到提高，其最大值为4 344 W，出现在t=12.9 h。在整个昼夜循环里，优化航迹使太阳能无人机的净吸收能量提高了9.2%。

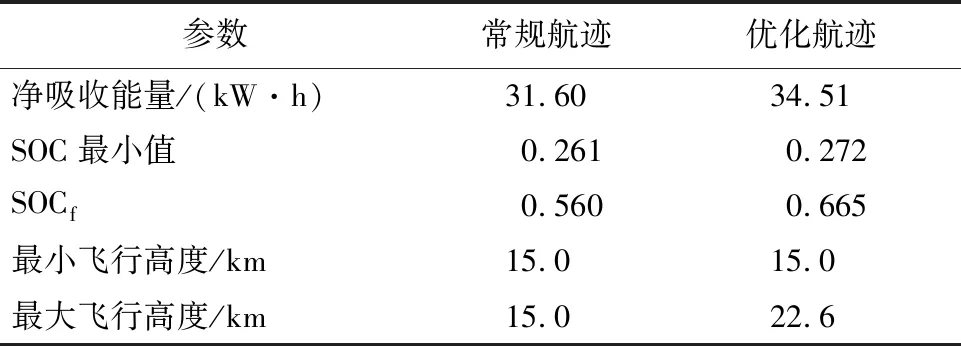
表6 仿真结果对比Table 6 Comparison of simulation results

图2 常规航迹及优化航迹功率Fig.2 Power of common flight path and optimized flight path

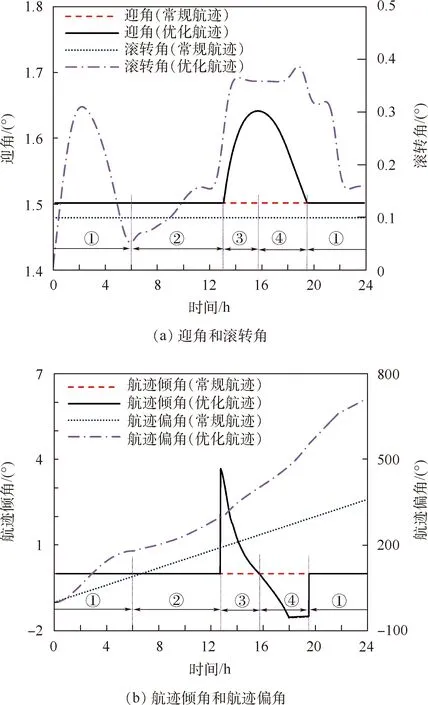
在常规航迹中，无人机定高定速飞行，电机提取功率始终为1 104 W。而在优化航迹中，自t=12.9 h开始，电机提取功率增大至和太阳能电池输出电功率一致。当12.9 h

常规航迹与优化航迹在水平面的投影如图3所示。

阶段①：定高巡航

由于Psc=0 W，常规航迹和优化航迹都旨在使功率消耗最小化，因而在这一阶段中，2种航迹的状态变量和控制变量几乎相同。如图4所示，无人机在任务允许的最低高度(15 km)以平飞最小功率对应的有利速度(23.3 m/s)飞行。迎角始终为1.5°，航迹倾角始终为0°，分别见图5(a)和图5(b)。螺旋桨推力约为34.4 N，储能电池放电功率为1 104 W。

图3 航迹在x-y平面内的投影对比Fig.3 Comparison of flight path projection on x-y plane

图4 常规航迹与优化航迹的飞行高度及飞行速度对比Fig.4 Comparison of flight altitude and velocity between common and optimized flight path

为了尽可能降低需用功率，滚转角本应为0°。但为了满足结束时刻的边界条件，同时为了在下一阶段获取更多的能量，无人机维持较小但不为0°的滚转角以改变航向(见图5(a))。在该阶段结束时刻，航迹偏角约为180°，如图5(b)所示。

该阶段结束的标志为：Psc>0。

阶段②：平飞充电

与阶段①相似，无人机依旧在任务允许的最低高度(15 km)以平飞最小功率对应的有利速度(23.3 m/s)飞行，如图4所示。当Psc>Pm时，利用剩余功率给储能电池充电。随着Psc逐渐增大，当t=12 h时，达到最大充电功率3 179 W，如图2(b)所示。

为了增加太阳能电池板吸收功率，无人机以较小的滚转角来改变航向，通过这一方式，太阳能电池获取的能量提高了0.99 kW·h。

该阶段结束的标志为：SOC达到最大值0.9，如图6所示。

图5 常规航迹与优化航迹的迎角、滚转角、航迹倾角和航迹偏角对比Fig.5 Comparison of angle of attack, roll angle, flight path angle and heading angle between common and optimized flight path

阶段③：爬升飞行

由于储能电池已经充满电，无人机利用剩余功率爬升，初始爬升率为1.5 m/s，初始爬升角为3.6°。随着Psc的减小及Pm的增大，爬升率逐渐减小，在t=15.7 h时刻，爬升率减小至0 m/s，无人机到达最大高度(22.6 km)。在爬升过程中，飞行速度接近于当前高度对应的有利速度。爬升过程持续2.8 h，无人机利用7.6 km的高度差储存了2.7 kW·h的重力势能。

值得注意的是，飞行高度越高，平飞需用功率越大，在总太阳能一定的情况下，飞行需用功率越小，剩余功率越大。因此，为了使储能电池剩余电量最大化，应在充满电之后再爬升，而不是爬升到一定高度之后再充电。

和阶段②类似，通过调整滚转角和航迹偏角，使得太阳能电池获取的能量增大了1.54 kW·h。

该阶段结束的标志为：剩余功率为0 W。

图6 常规航迹与优化航迹的储能电池电量状态对比Fig.6 Comparison of battery pack state of charge between common and optimized flight path

阶段④：下降阶段

太阳能不足以维持在当前高度继续平飞，无人机开始下降。在日落前，无人机保持有动力下降，充分利用太阳能以争取尽可能长的下降时间，在这段时间里，通过改变飞行姿态，太阳能电池获取的能量提高了0.38 kW·h。在日落之后，利用重力势能无动力下滑。整个下降过程持续3.6 h。

该阶段结束的标志为：无人机到达任务允许的最低高度。

在阶段④结束后，阶段①重新开始，形成一个完整的循环。

在阶段③和阶段④，无人机存储并利用重力势能，代替了部分储能电池的作用。在这4 个阶段里，无人机不断调整滚转角和航迹偏角以满足结束时刻的边界条件，更重要的是通过这种方式，太阳能电池吸收功率得到了提高。

4 结 论

本文提出了高空太阳能无人机三维航迹优化方法，针对一种典型的点到点飞行任务进行了航迹优化，并与常规定高定速航迹进行了对比。主要结论如下：

1) 高斯伪谱法适用于高空太阳能无人机航迹优化问题。

2) 通过调整飞行姿态，可以使高空太阳能无人机的净吸收能量提高9.2%。

3) 结合调整飞行姿态和改变飞行高度两种措施能够获得更大的能量优势，使储能电池剩余电量提高18.8%。

4) 为了使储能电池剩余电量最大化，应在储能电池充满电之后再爬升。