基于多子块协同单尺度Retinex的浓雾图像增强

高原原， 胡海苗

(1. 中国电子科技集团公司信息科学研究院， 北京 100086； 2. 北京航空航天大学计算机学院, 北京 100083)

随着计算机性能的提高和多媒体技术的快速发展，以及人们对社会公共安全的日益关注，大量的监控摄像头应用在智能车辆、停车场、社区监控、海陆交通监控、城市安保和军事侦察等重要场所[1-3]。然而，视频监控系统对天气条件非常敏感，尤其是在出现频繁且分布区域广泛的雾天。雾天情况下，图像容易出现对比度降低、细节特征被覆盖、色彩严重失真等现象[4]。这些低质量的图像因为信息量不足，严重影响了户外计算机视觉系统的效用。退化的雾天图像不仅会影响目标的观测，还会使识别、取证、事件分析变困难。因此，研究如何利用图像处理技术消除雾天对成像系统的不利影响是计算机视觉领域中一个非常有意义的问题，具有广阔的应用前景。

现有图像去雾算法从是否利用物理模型的角度，可粗略分为2 类：基于图像恢复的方法和基于图像增强的方法。基于物理模型的雾天图像恢复是考虑雾天图像退化原因，利用大气散射模型通过求解模型中的相关参数，反解出无雾图像，从而改善图像质量，其目的在于还原真实无雾场景。基于图像增强技术的去雾是不考虑图像退化的原因，仅考虑图像呈现的低对比度、低饱和度等特征，通过对图像有用信息进行增强同时抑制或者去除不需要的信息，来改善图像质量、提高图像的清晰度。

基于物理模型的雾天图像恢复方法主要包括基于偏振特性的方法[5-8]、基于偏微分方程的方法[9-10]、基于深度信息的方法[11-14]、基于先验知识或假设的方法[15-20]和基于深度学习的方法[21-23]。

基于偏振特性的方法是以光的偏振特性为基础，依靠硬件的支持且需要多幅图像才能完成模型参数估计，具有局限性。而基于偏微分方程的方法和基于深度信息的方法通常需要一定程度的人工交互操作，无法做到自动处理。因此，日常监控系统的工程实践中并不常用。

基于先验知识或假设的方法是利用单散射模型中参数的特性，人为设置一些约束条件，从而使得参数可解，目前已取得了突破性的进展[15-20,24]。基于深度学习的方法不需要人工设计特征提取器，而是由机器自动学习获得，典型的工作包括：Cai 等[21]提出DehazeNet 网络结构，利用特殊设计的卷积神经网络来学习雾天图像的特征，解决手工特征设计的难点。Ren 等[22]考虑雾天图像的多尺度特征，提出多尺度卷积神经网络学习雾天图像的特征估计透射率。Li 等[23]利用变形的大气散射模型，提出All-in-One去雾卷积神经网络，它可从有雾图像直接估计无雾图像。

基于物理模型的雾天图像恢复方法虽然在解决问题的思路上存在区别，但是最终目标都是通过单散射模型求解无雾的图像。然而，单散射模型假设场景光辐射充足且非常均匀，适合描述薄雾条件下的场景成像过程。浓雾情况下，悬浮颗粒的浓度变大时，可见光的穿透能力变弱，地表场景光辐射出现衰减，若仍利用单散射模型进行去雾处理，图像会出现亮度偏低、细节凸显不明显的情况。

可见，浓雾图像更适合使用增强方法进行处理。图像增强方法忽略图像降质原因，主要以提升图像细节来改善图像清晰度。典型的雾天图像增强方法包括直方图均衡化方法(Histogram Equalization，HE)[25-29]、曲波变换[30]和Retinex算法。

直方图均衡化方法可对图像的像素值进行非线性重映射，从而重新分配像素值，使其尽可能地均衡分布，实现对比度的增强。典型的直方图均衡化方法主要包括全局直方图均衡化方法[25]、局部直方图均衡化方法[26]、限制对比度自适应直方图均衡化方法(Contrast Limited Adaptive Histogram Equalization，CLAHE)[27]、广义直方图均衡化方法[28]和内容自适应的直方图均衡化方法[29]。直方图均衡化方法以合并数量较少的像素为代价完成像素值的重新分布，这会造成细节信息的丢失或图像模糊。

曲波变换是在小波变换基础上发展起来的多尺度分析方法。Eriksson[30]利用曲波变换的优势，采用基于曲波的消失点检测对雾天图像进行了自动去雾处理。然而，该类方法将整幅图像作为一个整体进行操作，不能保证一些关注区域得到所需要的增强效果。

Retinex 算法通过分离图像的低频分量和高频分量，然后移除低频分量，调整高频分量动态范围，实现对高频分量的放大，来完成细节的突出显示。从单尺度Retinex(Single Scale Retinex，SSR)算法到多尺度Retinex (Multi-scale Retinex，MSR)算法，再到带颜色恢复的多尺度Retinex (Multi-Scale Retinex with Color Restore，MSRCR) 算法[31-33]。Retinex算法在图像浓雾去除中的应用取得了一定的成果。Retinex 可以在灰度动态范围压缩、细节增强和颜色恒定3方面达到平衡，对各种场景的雾天图像都适用，因而一直受到国内外学者的广泛关注[34-36]。

然而，Retinex 用于浓雾图像增强时，通过全局均值统计量来对高频分量的动态范围进行截断量化[31-32]，对浓度分布均匀的雾天图像处理效果较好。当浓度分布不均匀时，由于每个区域的最优动态截断并不统一，无法保证每个区域的增强效果。因此，本文提出多子块协同单尺度Retinex算法，通过结合局部统计信息，获取多个局部最优的增强图像，再融合多个局部最优的图像获得最终的增强图像。实验结果表明，本文方法能够有效去除图像中浓雾的影响，并保证去雾后图像的亮度保持在适合人眼观察的范围。

1 单尺度Retinex算法及其问题分析

1.1 单尺度Retinex算法

Retinex算法中，图像可表示为低频分量和高频分量的乘积形式：

I(x,y)=L(x,y)R(x,y)

(1)

式中:I为采集设备获取的图像信息；L为不受关注的低频分量；R为能够体现物体真实细节特征的高频分量；(x,y)为像素的位置。利用Retinex算法实现图像对比度增强和色彩复原过程中，如何去除低频分量获取图像高频分量是其中一个关键环节。

应用最为广泛的单尺度Retinex是由中心/环绕理论发展而来，核心思想是：每个像素所包含的不受关注的低频分量是通过赋予其邻域像素不同的权重来进行估计的，权重的取值由一个函数来确定。数学表达式形式为

L(x,y)=I(x,y)*G(x,y)

(2)

式中：“*”表示卷积运算；G(x,y)为中心/环绕函数，通常采用高斯函数，公式如下：

(3)

∬G(x,y)dxdy=1

(4)

式中:κ为归一化因子；c为高斯函数的尺度参数。

为便于计算，将式(2)两边取对数，单尺度Retinex提取高频分量rSSR过程可表示为

rSSR(x,y)=log(R(x,y))=

log(I(x,y))-log(G(x,y)*I(x,y))

(5)

经过式(5)的处理，图像高频分量被提取，但对将其作为最终的增强结果并不适合观察，如图1(b)所示。接下来，还需对高频分量进行截断量化拉伸。首先，计算出高频分量的均值Mean和均方差Var，得到动态范围的截断值Min和Max：

Min=Mean-Dynamic·Var

(6)

Max=Mean+Dynamic·Var

(7)

式中：Dynamic为动态范围控制参数。然后，对高频分量进行线性映射，获得最终增强后的图像Value：

(8)

量化拉伸后结果如图1(c)所示，显然，与图1(b)比较，其动态范围更合理，更适合观察显示。

1.2 问题分析

传统的单尺度Retinex算法易于实现，且具有较好的图像增强效果，但其仍具有如下的缺陷：利用全局均值统计量来进行高频细节信息动态范围调整并不适合所有图像，因为当雾气浓度分布不均匀时，每个区域的均值差别较大，最优动态截断范围并不一致。

图1 单尺度Retinex处理结果Fig.1 Processed result of single-scale Retinex

如图2所示，当利用浓雾区域(图2(a)中下方矩形区域)的均值统计量计算动态截断范围时，浓雾区域去雾更为彻底(例如：图2(b)中工人的腿部)，但薄雾区域却出现了过增强(例如：图2(b)中图像顶部)。当利用了薄雾区域(图2(a)中上方矩形区域)的均值统计量计算动态截断范围时，薄雾区域未出现过增强，但浓雾区域去雾却不彻底。

图2 利用不同局部均值统计拉伸量化后结果Fig.2 Stretched quantization result using different local mean statistics

2 多子块协同单尺度Retinex算法

针对第1节关键问题，本文提出基于多子块协同单尺度Retinex 算法，该算法将图像划分为多个子块进行均值统计并计算动态截断值，再利用各截断值分别获得多个局部最优的增强图像，最后，融合各增强图像获得最终的增强结果。算法流程如图3所示。下面对关键部分的实施细节进行介绍。

1) 高频细节信息分解：本文将图像分解为低频分量和高频分量所采用方法与传统单尺度Retinex思想一样。只不过，为了抑制光晕，所用低通滤波器选用保持边缘滤波器-引导滤波器[37]，获取的高频细节分量为rSSR。

2) 多子块划分：雾气的浓度通常具有一定的规律性，呈现连续变化的趋势。为了使不同浓度的有雾区域尽可能地聚集到同一个子块且不影响运行速度，本文在水平和垂直方向上将图像划分为M行和N列。值得注意的是，划分子块越多雾气浓度划分越准确，但子块过小又会影响动态截断效果，因此，一般情况下M和N的取值应满足：

图3 基于多子块协同的单尺度Retinex算法流程Fig.3 Flowchart of multi-block coordinated single-scale Retinex algorithm

(9)

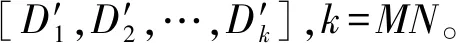
3) 多个动态截断值获得多幅增强图像：对每一高频细节分量子块rSSRn，n=[1,2,…,k]，统计其均值Meann和均方差Varn，并计算出动态范围的截断值Minn和Maxn：

Minn=Meann-Dynamic·Varn

(10)

Maxn=Meann+Dynamic·Varn

(11)

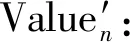
(12)

4) 图像融合：为了在图像细节增强和图像过增强之间寻找平衡点，本文最后将多个局部最优的增强图像进行线性加权组合，其数学表达式为

(13)

式中：r为多子块协同单尺度Retinex的输出结果；wn为第n个局部最优增强图像的权重，满足条件：

(14)

一般情况下w1=w2=…=wk=1/k。

3 实验结果与分析

为了验证本文算法的效果，本节将展示与典型图像去雾算法的对比结果。现有基于图像增强的图像去雾方法效果较好的主要有基于直方图均衡化的方法和Retinex算法。由于基于直方图均衡化的方法对浓雾图像的清晰度提升有限，本文取经典Retinex算法进行对比。此外，本文还提供了基于引导滤波的暗原色(Dark Channel Prior based on Guided filter，GDCP)算法[37]、Haze-line算法[20]和DehazeNet算法[21]的结果。GDCP算法是暗原色算法的改进，利用局部先验知识进行图像去雾，公认效果较好，使用最为广泛。Haze-line是利用全局先验进行去雾的算法，有利于图像去雾后防止色彩过饱和。DehazeNet是基于深度学习的去雾算法，由机器自动学习获得雾天图像特征完成去雾，解决了手工设计特征的问题。另外，为了验证本文算法改进单尺度Retinex的必要性，还提供了经典Retinex算法的结果进行对比。

主观评价方法的结果完全由人眼的主观感受决定，能够比较准确地反映视频的质量，但却无法定量测量。本文算法主要用于提升图像细节和边缘，因此，为了验证去雾结果的客观效果，本文利用信息熵(h)[38]、新增可见比(e)和可视边缘梯度信息(γ)[39]来对增强后图像进行客观质量评价。去雾效果对比示例如图4～图6所示。

图4 去雾效果对比示例1Fig.4 Example 1 of defogged result comparison

图5 去雾效果对比示例2Fig.5 Example 2 of defogged result comparison

图6 去雾效果对比示例3Fig.6 Example 3 of defogged result comparison

GDCP算法基于单散射模型，场景光辐射的衰减被忽略，较适合薄雾图像，处理浓雾图像时，图像亮度无法得到保证。如图5(c)所示，图像虽然实现了去雾，但是亮度明显变低，细节难以辨识。Haze-line算法根据雾天图像中相同颜色的像素分布在一条直线的规律，通过聚类找到许多雾线，并假设半径最长的点透射率为1，反解出无雾图像。然而，半径最长的点透射率不一定是1，所以会残留较多雾气，如图4(d)、图5(d)所示。DehazeNet算法对大量有雾和无雾图像对进行训练，利用了深度学习的优势，但其仍基于单散射模型。因此，利用DehazeNet算法进行浓雾图像的去除会出现去雾失败的情况，如图4(e)和图6(e)所示。经典Retinex算法和本文算法不考虑退化因素，从增强的角度对图像进行清晰化，从灰度动态范围压缩、细节增强和颜色恒定几个方面展现出了优势。而且，由于本文算法考虑了不同区域动态截断值不同的特性，进行了多个子块协同处理，因此，去雾效果较Retinex算法更好，如图4(f)和图6(f)所示。

上述主观评价反映了图像增强的视觉质量。为了对图像质量进行定量的比较，还需对处理后图像进行客观评估。客观质量评估主要用于对图像的某些重要特征进行定量的描述。表1～表3给出了上述信息熵(h)、新增可见比(e)和可视边缘梯度信息(γ)的计算结果，每幅图像的最优结果已加粗标注。其中，新增可见比和可视边缘梯度信息是专门用于去雾结果盲评估的评价指标。

信息熵用来描述图像的平均信息量，在不引起失真的情况下，其值越大代表所含的细节越丰富。从信息熵的对比结果中可以看出，本文算法的信息熵并非最高，这是因为，Retinex算法采用动态截断的方法进行量化拉伸得到最终的增强结果，会有部分信息量的损失，但仍优于对比的大多数算法。

新增可见比和可视边缘梯度信息是衡量细节增强情况的指标，通常，其值越大表明去雾后图像可视边缘和细节的强度越大、数量越多。从表1～表3的结果可以看出，本文算法要明显优于其他对比算法。这意味着，虽然部分算法增强后细节要多于本文算法，但可视能力却要弱于本文算法。

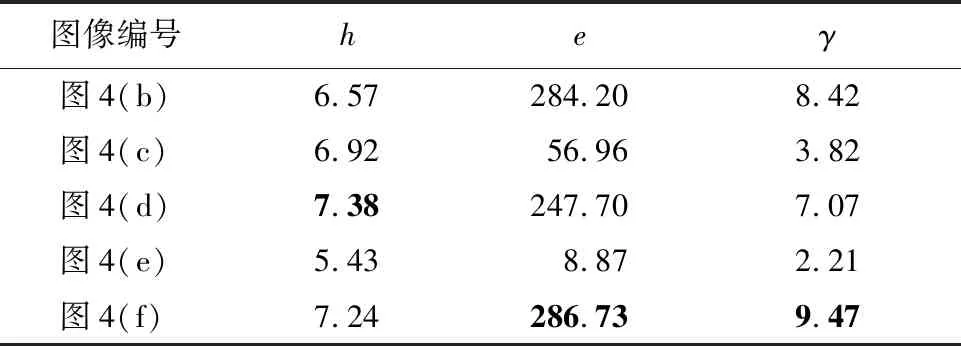
表1 图4去雾后客观指标评价结果Table 1 Objective indicator evaluation results of defogged images in Fig.4

表2 图5去雾后客观指标评价结果Table 2 Objective indicator evaluation results of defogged images in Fig.5

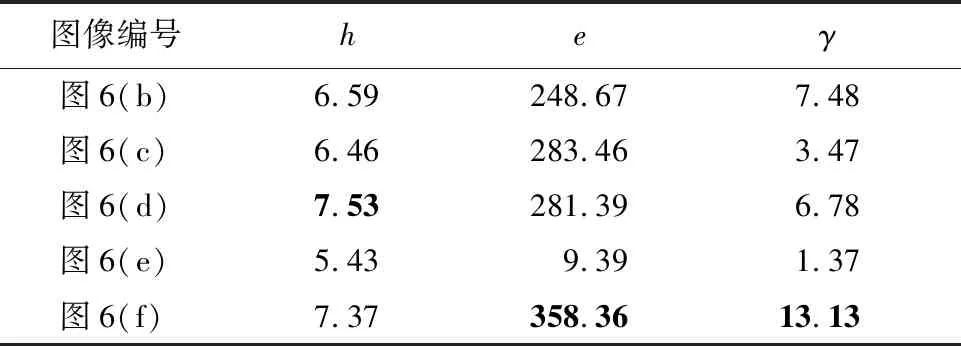
表3 图6去雾后客观指标评价结果Table 3 Objective indicator evaluation results of defogged images in Fig.6

4 结 论

本文在单尺度Retinex算法基础上提出了多子块协同单尺度Retinex浓雾去除算法。经实验验证，得到：

1) 本文算法考虑了雾气不均匀的浓雾图像特征，针对每个局部的均值统计量不一致的情况，改进了经典单尺度Retinex量化拉伸的过程，从而增强了Retinex算法的鲁棒性。

2) 本文算法可以实现较优的去雾性能，与其他典型去雾算法相比有所提高。

通过实验验证，本文算法的图像去雾效果得到了提升，一定程度上提高了图像的清晰度。在未来，可以改进该算法，增加多个增强图像融合的自适应性，从而取得更好的去雾效果。