解后反思辨明结构，变式再练反馈学情——以一道期末卷几何综合题为例

☉江苏省如皋市搬经镇初级中学 丁广峰

研究解题是很多数学老师的兴趣，特别是对各地中考或者优秀地区期末试卷的研究是教研热点.近期我们在《中学数学（下）》关注到不少文章以一些地区的2018—2019学年度第一学期期末试卷考题为例，给出解题思路的突破，问题结构的回顾与反思，并有独到的教学设计和立意的解读，为深入开展解题教学研究提供了很好的视角.受到启发，本文也以某市八上期末试卷上一道几何综合题为例，先解析思路，并跟进教学建议，供研讨.

一、考题思路解析与回顾反思

考题：（某市八上期末试卷，最后一题）已知∠ABC=60°，AB=BC，D是BC边上一点，延长AD到点E，使得AD=DE，连接CE，过点D作BC的垂线，交CE的垂直平分线于点F，连接BF.

（1）如图1，当点D与点C重合时，证明：BF=2DF.

（2）如图2，当点D不与B、C两点重合时，（1）中的结论是否还成立？请说明理由.

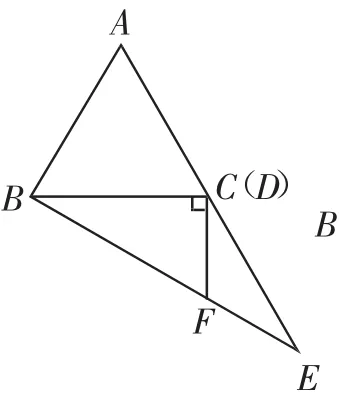
图1

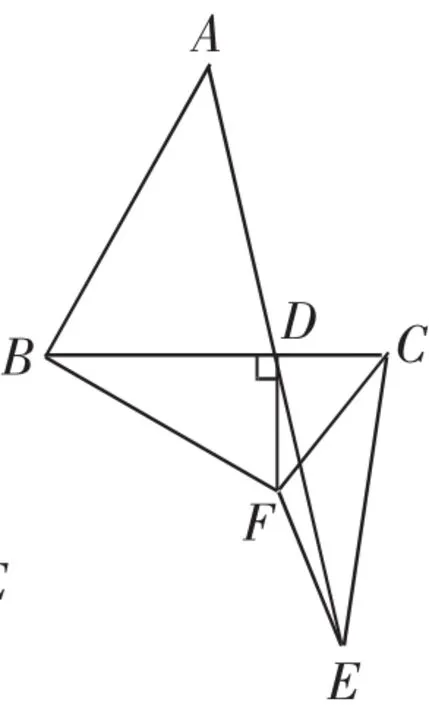
图2

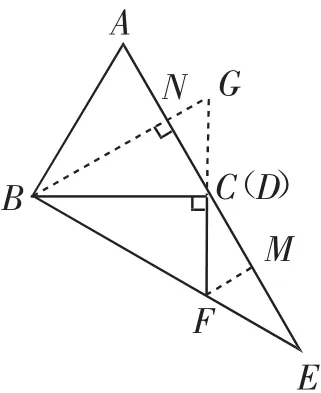
图3

思路解析：（1）这一问因为点D与点C重合，所以证法较多，下面概述三种证法.

证法1：容易得到△ABD是等边三角形.AB=BD=AD，∠ADB=60°.由AD=DE，可得BD=DE，所以∠BED=∠ACB=30°. 由DF⊥BD于点F，得∠BDF=90°，则∠FDE=30°.由点F在DE的垂直平分线上，得DF=EF，故∠FED=∠FDE=30°.所以∠FED=∠BED.又由题意知点B、F在AE的同侧，所以B、E、F三点共线，所以∠FBD=∠BED=30°，即在Rt△BDF中，BF=2DF.

证法2：如图3，过点B作BN⊥AD交FD的延长线于点G，过点F作FM⊥DE于点M，可得∠GNC=∠FMC=90°.同样先证得△ABD是等边三角形，得到AB=BD=AD，ND=AD，AN=ND，∠ABG=∠DBG=∠ABC=30°.结合点F在DE的垂直平分线上，有DM=DE.由AD=DE，得ND=MD，进一步证得△NGD △MFD，则GD=FD.由DF⊥BD，得BG=BF且∠BDF=90°，则∠DBG=∠DBF=30°，即BF=2DF.

证法3：如图4，延长FD至点G，使得DG=DF，连接BG、AG.

由于DF⊥BC于点D，∠BDF=90°，所以BC垂直平分FG，则BG=BF，∠DBF=∠DBG.又AD=ED，∠ADG=∠EDF，可证得△ADG △EDF，于是AG=EF.由于点F在CE的垂直平分线上，点D与点C重合，所以DF=EF，DF=AG.再结合已知AB=BC，可得出关键结论：△ABG △DBF，所以∠ABG=∠DBF，∠ABG=∠DBG=∠ABC=30°，则∠DBF=30°，从而BG=2DG，即BF=2DF.

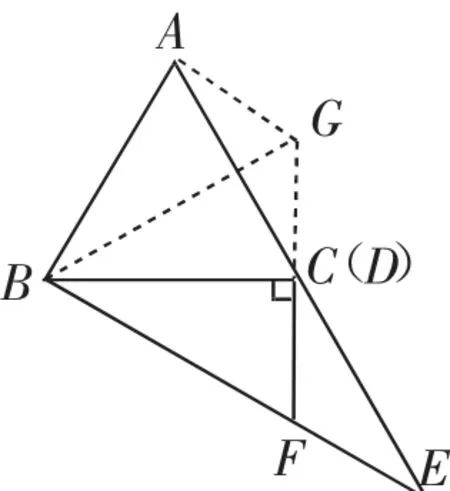
图4

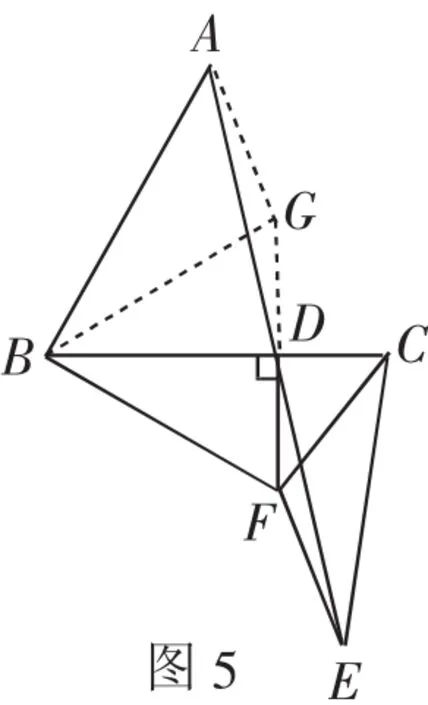
图5

（2）由（1）中“证法3”可以获得证明思路，如图5，延长FD至点G，使得DG=DF，连接BG、AG.由题意易得∠BDF=90°，BG=BF，∠DBF=∠DBG.又AD=ED，∠ADG=∠EDF，可证得△ADG △EDF，则AG=EF.结合点F在CE的垂直平分线上，所以FC=FE，AG=CF.又AB=BC，所以可得关键步骤△ABG △DBF，则∠ABG=∠CBF，∠ABG=∠DBG.结合∠ABC=60°，得∠GBD=30°，所以∠DBF=∠GBD=30°，即BG=2DF.

回顾反思：这道考题主要难点在第（2）问，虽然延续第（1）问“证法3”获得一种证明，但这道考题的深层结构还有待深入探究，以下再提供一些研究角度.

思考1：点F的运动路径是什么？

解析：结合（1）、（2）的证明可以发现，∠DBF=30°，可见点F在一条线段上运动，这条线段就是图1中的BF.

思考2：问题还可以怎样的方式呈现出来？

如图6，等边三角形ABC、BEF有公共顶点B，且BC平分∠EBF.设边EF交BC于点D，连接AD并延长到N，使DN=AD，延长AC到M，使CM=AC.连接FC、FN、FM.

经过推证，我们可以得到与考题等价的一些结论，如点B、F、M在同一直线上，FC=FN（可以连接AE分别证△ADE△NDF，△ABE △CBF），CD为△AMN的中位线，等等.

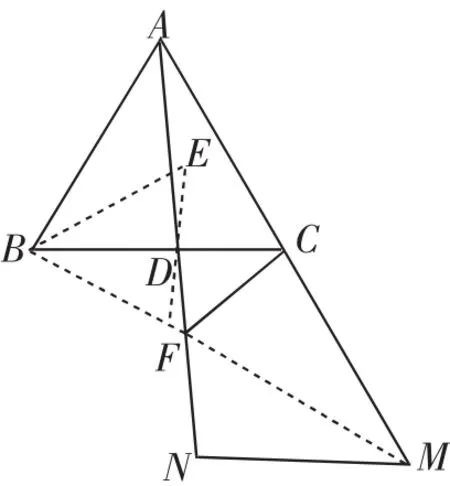
图6

二、关于几何综合题的教学思考

1.注重审题教学，明辨题设结论

几何解题教学的关键是在审题阶段对问题的条件与结论想清辨明，比如，题中有了哪些确定的条件？求解目标或方向是什么？以上面的考题为例，有哪些确定的条件或元素，都需要认真看清想明，条件中能解读出一个等边三角形ABC，而点D则是线段BC上一个动点，另外能确定的还有AE=2AD，点D、E的位置都是不确定的，但是它们又有一定的运动轨迹，如相应的E点在与BC平行位置上的一条线段上运动，而F点的运动路径是一条线段，这些都需要在审题、解题进程中得到明确.

2.加强解后反思，看清问题结构

罗增儒教授在解题研究的诸多论述中都十分重视“回顾反思”环节，有时一个看似简单的数学习题能写出几千字的回顾反思，并将原问题的深层结构、可能拓展等做到让人叹为观止的地步，罗教授常常说：解题之后缺少必要的回顾反思常常是“入宝山而空返”.这也就是我们在上面解后回顾阶段提出两个“思考”的原因，特别是“思考2”，将问题的生成重新构思，从两个共顶点的等边三角形出发，生成考题结构，而考题则是在此基础上删减、隐藏一些非必要的线条，改头换面，使得问题以另一种方式渐次呈现.这事实上也是很多几何综合原创命题的一种常用技术.教师也可以在平时的试题命制中进行尝试，训练自己的命题能力，对于教学设计中的例题改编、习题变式、作业设计也是非常有益的.

3.重视变式再练，有效反馈学情

根据课堂观察，很多试卷讲评课、专题复习课常常因为教学时间所限，缺少对本课内容的变式检测与及时反馈学情.我们认为，备课打磨时，要充分考虑教学时间的分配，将变式再练习题的时间预设到教学进程中，对本课所讲评的重点内容、主要方法、转化策略在最后变式检测环节进行训练，知易行难，下面给出本文考题的一个变式问题，可以作为讲评之后的跟进反馈.

变式问题：如图7，已知等边三角形ABC，点D在AC的延长线上，且CD=AC，点H是边BC上一动点，点E在射线AH上，且EH=AH，连接BD、DE，过点H作HG⊥BC，交BD于点G，连接GC、GE.

（1）求证：BG=2GH；

（2）求证：GE=GC.

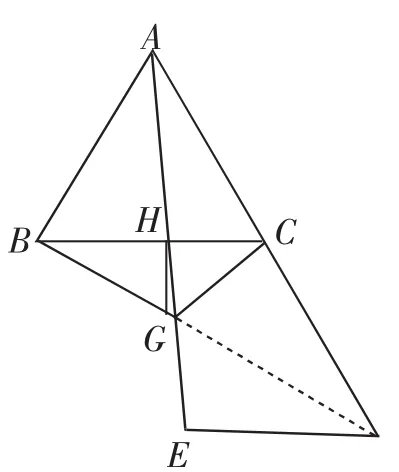
图7

三、写在后面

2011年颁布的义务教育阶段课程标准中，对第三学段平面几何教学内容做出明确的要求，可以发现平面几何教学内容和要求是非常低的，弱化繁难几何内容与证明技巧是国家要求.然而我们注意到不少地区以所谓不能弱化平面几何教学的片面理解和个性化执行，在本地区的中考或期中（末）考试中随意拔高平面几何习题的难度，使得本地区师生不得不投入大量精力训练一些繁难偏怪几何习题，而平面几何的学习成本并不一定会与繁难几何习题证明能力的提升成正比，因为较难的平面几何习题的解题能力确实与每个研习者个性适应性高度相关，让“全样本”学生都在地区平面几何难题的引领下钻研平面几何习题，是值得商榷的命题导向，也是值得一些地区命题专家们反思的.