根据教材例题，开发一题一课

☉安徽省合肥市行知学校 吴子赟

近日，在研读中学数学专业期刊过程中，发现刊发了大量的基于中考压轴题的“一题（图）一课”的设计案例，即首先在认真分析的基础上给出该中考试题难点的突破方法及求解思路，然后开发设计成可以在一个课时内完成的教学案例，读后受益匪浅.笔者在近期教学中思考：上述方式针对中考专题复习有效，那么，能否在日常教学中（比如一个知识点讲完后的综合复习课或单元复习课）中适用呢？带着这样的想法，开展了基于教材例题的“一题（图）一课”设计的有益尝试.下面简单介绍，并给出一些初步的思考，不当之处，敬请指正.

一、教材例题

如图1，E是正方形ABCD中CD边上任意一点，以点A为中心，把△ADE顺时针旋转90°，画出旋转后的图形.

说明：上述例题是在学生自主探究得出旋转的三条基本性质后教材中出示的一道例题，主要考查学生对新知的掌握程度和灵活应用情况，教材中的方法是：首先运用“对应点与旋转中心所连线段的夹角等于旋转角”确定了点A和点D旋转后的对应点，然后运用“旋转前、后的图形全等”这一性质作出了点E的对应点E′，进而将问题解决，显然对旋转的另一性质“对应点到旋转中心的距离相等”没有涉及.

二、“一题（图）一课”设计

1.解答例题

在上述例题的题干后面增加提示语：你能想到几种作法？每种作法的依据是什么？先独立思考，再与同伴交流.

设计意图：从教材例题出发，引导学生多角度思考问题.一题多解需要用到旋转的不同性质，进而加深学生对新知的认识.同时，在学生回答后，引导学生积极进行解题后的反思，比如，例题的解答依据是什么？解答本题你还有什么方法？依据是什么？引导学生深刻认识知识的本质，进一步加深学生的印象.

教学预设：还可以过点A作AE的垂线，截取AE′=AE（如图2），应用“对应点到旋转中心的距离相等”这一性质将问题解决，弥补教材的不足.

图1

图2

2.变式练习

（1）如图3，四边形ABCD是正方形，E、F分别是DC和CB延长线上的点，且DE=BF，连接AE、AF、EF.

①填空：△ABF可以由△ADE绕旋转中心点，按顺时针方向旋转_____度得到；

②若BC=8，DE=6，则△AEF的面积为_______.

（2）如图4，在四边形ABCD中，∠BAD=∠BCD=90°，AB=AD，AE⊥BC于E，若AE=4，则四边形ABCD的面积为_____.

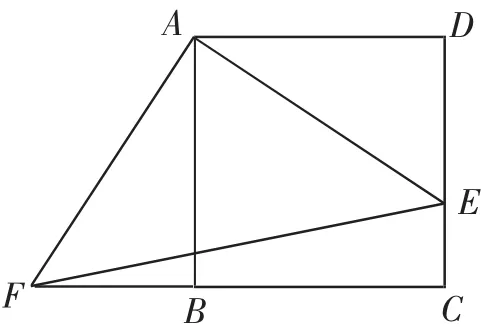
图3

图4

设计意图：上述变式练习针对教材例题采用变式设计的典型方法（变条件）进一步巩固学生对图形中所蕴含结论的理解，其中变式练习第（1）题第①问直接针对教材例题给出，第②问考查学生简单的推理能力（在△ADE △ABF的基础上，进一步得到∠FAE=90°，从而发现问题的本质，即△AEF是等腰直角三角形）；第（2）题考查学生一定的逆向推理能力及转化意识，将未知问题转化为熟悉的问题进而解决问题.

3.自主探究

（1）如图5，在正方形ABCD内作∠EAF=45°，你能得到哪些结论？

设计意图：通过增加特殊角的形式改变条件，进而引发图形的变化，随之而来的是一系列结论的变化.同样，开放式的问题设计引导学生多角度思考问题，培养学生良好的思维能力，为培育学生的理性思维进行一定的尝试.

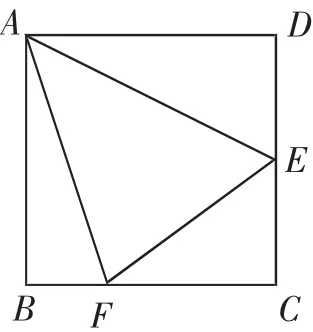
图5

图6

教学预设：

①三角形全等：△AEF △AHF；

②角：∠AFH=∠AFE（AF平分∠HAE）、∠AED=∠AHF=∠AEF；

③线段：EF=DE+BF；

④面积：S△ABH+S△ABF=S△AEF.

（1）—1：如图7，在正方形ABCD内，∠EAF=45°，AG⊥EF，求证AG=AB.

（1）—2：如图5，若正方形ABCD的边长为1，∠EAF=45°，则△CEF的周长为_____.

设计意图：加强学生对上述四个结论的理解和灵活运用，比如（1）—1需要用到结论②（也可以从面积相等的角度得出结论），（1）—2需要用到结论③.

图7

图8

（2）如图8，在正方形ABCD内，∠EAF=45°，对角线BD分别交AE、AF于点M、N，试探究BN、MN、DM的数量关系，并证明你的结论.

设计意图：采用变式的另一种方式，增加特殊线段：对角线；巩固教材例题的典型方法：旋转.

教学预设：将△ADM绕点A顺时针旋转90°，得到△ABM′，进而得到一个直角三角形M′BN，再结合三角形全等可以得到BN2+DM2=MN2（如图9）.

（3）追问：第（1）题中第③个结论的逆命题成立吗？第（2）题得到的结论的逆命题成立吗？

设计意图：提出更具有挑战性的问题，使“不同的学生在数学上得到不同的发展”.

图9

三、两点思考

1.教材例题要具有生长性

通过上述案例的介绍可以看出，围绕一道教材例题，从变条件、变结论、变图形三个角度开展变式练习，设计形成“一题（图）一课”，这需要所选的教材例题具有生长性，否则的话不能达到预期的教学效果.

从教材例题出发，各变式练习渐次生长，互为依托，使课堂教学逻辑连贯，思路清晰，实现了课堂教学的优质、高效，同时，这样的设计为学生后续开展自主学习打下了基础，与中国学生发展核心素养中提出的“学会学习”是不谋而合的.

2.问题设计要具有开放性

在上述案例中，通过设计开放性的问题，达到锻炼学生思维能力的目的，比如，所提问题中的：你能想到几种作法？你能得到哪些结论？等等.这样的尝试给学生打开了一扇窗，开阔了学生的思路，让学生的回答具有开放性，比如，学生针对教材例题给出的第二种方法，以及（1）—1的两种不同思路，这使课堂教学具有了一定的开放性，实现了课堂教学的“百花齐放”.