在游戏中学习，在学习中提升——以“算24”引导有理数混合运算为例

☉浙江省桐庐县实验初级中学 王良弟

作为数学教师，经常碰到这样一种现象：许多学生对一些题目感觉会做，但就是不能得出正确的答案，特别是有些涉及计算类的题目，感觉很可惜，老师称之为“低级错误”，不少学生则将其归咎为“粗心大意”或“一时疏忽”，误以为只要在解题时细心一些就可以避免，然而我认为错误背后的原因是概念不清，如-32与（-3）2是不一样的，或是算法、算理没有牢固掌握.因为计算不过关，不仅极大地影响了学生的学习成绩，也严重地挫伤了学生学习的积极性，制约了数学教学质量的提高和学生数学素养的发展，所以七年级上学期有理数的运算非常重要，但学生总认为非常简单，不重视，而且嫌烦.在课间，我偶然发现学生在玩计算“24”的游戏，笔者也产生了浓厚的兴趣.作为备课组长，在集体备课时向学科组成员提出，安排上一节示范课.在学科组成员热情洋溢的研讨中，认为本节课堂教学活动课，可以安排多个活动场景以达成解决有理数混合运算的目的.在讨论过程中，学科组成员一致认为，一是在课堂上设计计算24点的游戏情境，让学生体会有理数混合运算符号和顺序的关键性，通过游戏活动，有效开启学生多种感官的活动，如视觉、听觉，营造一种和谐、愉快、宽松的探究氛围，激发学生强烈的学习欲望；二是创设一种方式，能够通过课堂教学让学生明确掌握本节课要学习的知识点，完成教学目标，本节课的一个重要内容就是加入乘方运算，让学生在数的运算的二级运算基础上拓展到三级运算.

学科组成员各抒己见，对本节课提出了不同的看法，最终达成了共识，并提出了一系列的课堂设计方案，通过磨课，笔者上了一节公开课，将一些值得推广的教学过程记录在案，并做了一些肤浅的解读，旨在让广大一线同行共同探讨.

一、用游戏“算24点”创设情境，激发学生探究新知的欲望

师：同学们，今天大家先来做一个游戏“算24点”，以前玩过的举手，知道游戏规则吗？

有很多学生积极举起手来，说明这点燃了学生的探究热情，让课堂气氛热闹非凡.

师：现在就来赛一赛，看谁的计算速度快，谁的方法多.

拿出一副扑克中的一种花色，抽出四张扑克的点数：课前准备好的2、3、5、8.在集体备课时，成员就可以设计一些简单的方案，如：

（1）8×2+3+5=24；

（2）（5+3）×2+8=24；

……

学生积极行动起来.

师：如果加入乘方运算，你还有其他的计算方法吗？

课堂的质疑会让热闹的课堂平静下来，聪明的学生也会提出：（8-5）×23……学生有这样的想法不足为奇，在集体备课时可以预测到有些学生可能写出很多算式.

师：（赞扬）我们的学生给出的算式中出现了乘方运算，你们知道加入乘方后，有理数混合运算又会有什么样的法则吗？今天我们一起来探究“有理数的混合运算”.

设计解读：通过一种棋牌类益智游戏，根据数学运算符号的加入，让计算结果等于24，规则简单，学生自然而然会进入“套路”，这样能够大大激发学生的求知欲.创设这样的课堂情境是导入新课最有效的方式.

二、通过课堂中师生之间的互动，引导学生步入探求新知征程

1.师生之间互动得出有理数的混合运算法则

师：我们已经学过的数的加减是第一级运算，乘除是第二级运算，目前我们接触到的乘方就是第三级运算.为什么运算在不断升级呢？打个比方说，我们都玩过手机游戏，手机和游戏软件也会不断升级.在玩游戏时，升级的手机和没有升级的手机你会选择哪一种？

课堂上又有了学生的笑声、议论声.

生：喜欢用升级后的手机去玩游戏.因为升级后的手机比没有升级的玩起游戏来更过瘾、速度更快.

师：在多款手机中你会优先选择升级最高的那款进行游戏，有理数的混合运算法则也是如此.

有学生点头，并开始思考.

师：根据刚才提出的看法，谁能来说一说有理数的运算顺序？

教师展示运算法则的填空，学生举手抢答.

师：倘若算式中出现括号，括号内的算式就是升级后的手机，必须先进行运算.

2.通过课堂的例题引导，让学生熟知有理数的混合运算法则

再次强调有理数的混合运算法则，让法则植于学生的脑海.然后用电子白板出示例题.

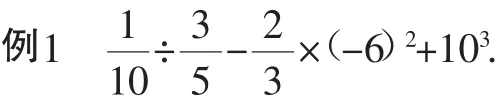
师：同学们，看一看：这个算式中包含了几种运算？想一想：最先该算什么？然后算什么？

学生思考，并有举手回答的，有的学生开始跃跃欲试.

师：其他同学还有不同想法吗？好，请同学们根据上面学过的有理数的运用法则，计算该式的结果，好吗？

学生着手进行计算.

师：（在巡视中进行说明）这个算式可以看成由三个部分组成，各组成部分通过加号或减号连接，各组成部分可以同时进行计算，运算乘方时底数和指数要清楚.

用电子白板出示.

师：同学们看看这道题与例1有什么区别，请同学们自己在纸上完成.

师：谁能解答这道题？

学生做完后，举手上台利用投影仪进行展示.

师：（当一个学生展示完后）还有没有同学与他的解法不同？也可以来展示.

学生举手上台利用投影仪进行展示，教师通过计算方法的对比进行课堂评价.

师：从以上的展示可以看出，根据题目特点选择最适宜的解法，尽量采用简便运算，而不一定要生搬硬套.

设计解读：通过两个例题让学生充分认知有理数的运用法则，有层层递进的关系.通过例2的解题方法，还可以让学生明确：可以按照今天给出的有理数运算法则，也可以按照乘法分配律，循规蹈矩是不可取的，要采用合理的运算，方法越简单越好.

3.通过课堂的小组对抗赛，让学生巩固有理数的混合运算法则

通过前面的两个例题，学生对有理数的运算法则有了基本的认识，然后可以通过课堂练习进行巩固.

［课堂练习］

设计解读：小组对抗赛可以激发学生探究的热情，可以凝聚团队力量，在取得成功的同时学生会自然产生自豪感、荣誉感，从而达到巩固知识获得运算技能的目的.

4.通过课堂的习题改错，让学生深化有理数的混合运算法则

精心设计4道改错题，放在四张扑克牌的背后，展示在电子白板上.

师：今天老师只给大家带来了扑克，看看白板上的扑克，后面都有一道改错题，哪位学生敢于挑战？

学生举手，请求挑战，上台翻开改错题进行讲解，教师及时纠错.

设计解读：此类改错题的计算较为复杂、易混，学生做题时出错几率较大，目的是对有理数混合运算法则的常见问题的警示，有利于学生扬长避短.

5.通过课堂小结归纳，让学生系统化掌握有理数的混合运算法则

通过例题、课堂练习和改错题的训练，学生对有理数混合运算的步骤有了较深刻的认识，但仍然需要教师对步骤进行进一步强化.

通过ppt播放解决有理数混合运算计算题的步骤：

（1）首先厘清算式中含有的项是什么.

（2）遵循法则考虑各项的运算顺序.

（3）同时计算的各项要结果同步，暂不计算的项应照搬不误.

（4）同级运算必须从左到右.

设计解读：课堂小结归纳是课堂巩固的重要环节，是知识潜移默化的有效途径，将有理数混合运算系统化和理论化，属于知识系统构建不可缺失的环节.

6.回到游戏“算24点”的原点，固化学生应用新知的思维

再次拿出扑克，抽出四种扑克，分别是（课前准备好）2、3、4、5，让学生在有理数式子中出现乘方的形式.

学生思考，同桌交流.

设计解读：激发学生在用中学数学的热情，将数学知识延伸到课余，形成数学大课堂，为生活服务.

三、写在最后

集体备课是一种集思广益，对课堂环节的推敲出现争执是不可避免的，但最终的尘埃落定还是要由不同班情和学情所决定，教师需要有驾驭课堂的能力.“算24”游戏为数学课堂带来的是妙趣横生的探究环境，让枯燥的有理数的运算变得丰富起来，在课堂结束时又再次回到“算24”的游戏，使课堂设计鲜活起来.在对三级运算进行说明时提出了“升级版”，与时代接轨，与学生的爱好接轨，使得知识更加清晰、自然.运算能力是一项基本的数学素养，通过贴近学生的素材情境，让学生掌握算法，理解算理，必将整体提升学生的数学素养，为学生的发展奠定坚实的基础.