中考几何探究性问题研究
☉江苏省宜兴市实验中学 刘 媚
中考数学中,几何问题几乎占据“半壁江山”.在几何试题中,几何探究性问题最引人注目,在中考中主要出现以下三类问题:图形变换问题、动态几何问题和类比探究问题.本文分别加以举例说明,供大家参考.
一、图形变换问题
图形变换问题主要包括图形的轴对称、图形的平移及图形的旋转.在涉及图形变化的考题中,解决问题的方法较多,关键在于解决问题的着眼点,从恰当的着眼点出发,再根据图形变换的特点发现变化的规律很重要.近几年各地的中考试题中,有较多问题需要利用图形变换进行思考和求解.这类问题能更好地综合考查考生的思维品质,并具有很好的选拔与区分功能,是一个炙手可热的中考数学命题热点.
例1(1)如图1,在直角三角形ABC中,∠ABC是直角,先绕着点B将△ABC逆时针旋转90°后,得到△A1BC1;再绕着点C将△ABC顺时针旋转90°后,得到△A2B1C.最后连接C1B1,那么C1B1与BC的位置关系为______.
(2)如图2,当△ABC的最大角为锐角,且∠ABC=α(α≠60°)时,把△ABC仿照(1)中的变换方法旋转α,再连接C1B1,这时C1B1与BC具有怎样的位置关系?请证明你的结论.
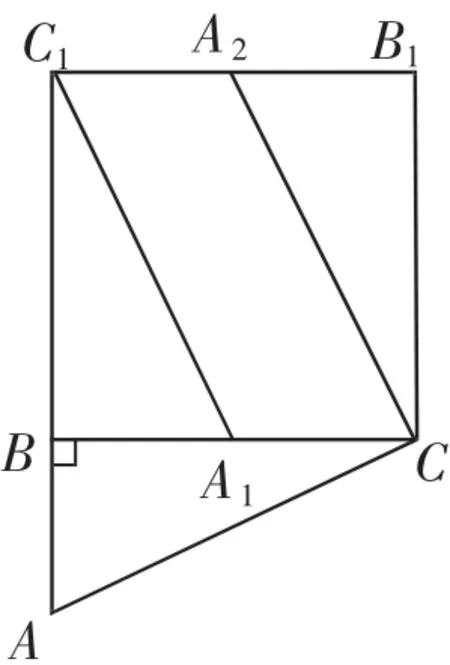
图1
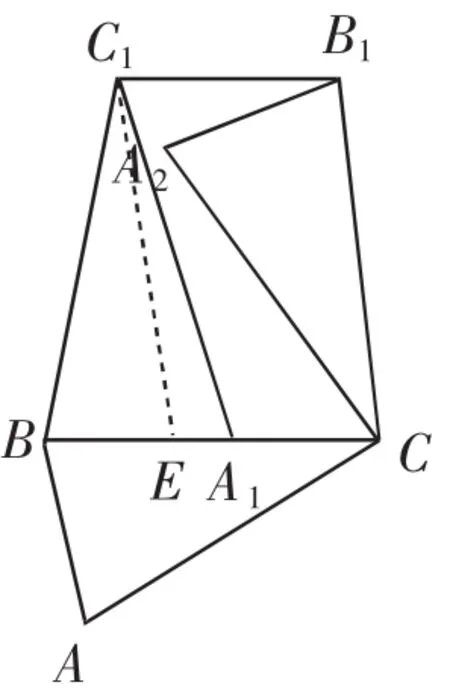
图2

图3
解析:(1)由旋转的有关性质,可知∠C1BC=∠B1CB=90°,BC1=BC=B1C,于是可推出CB1∥BC1,进一步可推知四边形BCB1C1是平行四边形,再由平行四边形的性质定理就可以推知所求的结论了.
(2)经过点C1作C1E∥B1C交BC于点E,由此得出∠C1EB与∠B1CB相等.根据旋转的有关性质知BC1=BC=B1C,且∠C1BC与∠B1CB相等,于是∠C1BC=∠C1EB.因为等角对等边,故C1B=C1E,进而C1E=B1C,于是四边形C1ECB1是平行四边形,最后由平行四边形的性质定理就可得到所求结论.
(3)设C1B1与BC之间的距离为h,根据已知条件就可得到相似比与面积比都等于底边的比,这样结论就容易得出了.
评析:本题考查旋转变换.图形变换是中考命题中的热点问题,也是难点问题,尤其是旋转变换.在具体问题的解答过程中,我们应恰当应用旋转变换的性质,抓住图形特征,开阔思路,化难为易.从本题可以看出,对于图形的旋转变换问题,我们不仅要学会借助推理,更要借助直觉和观察,在分析问题时要变换视角,让数学直觉更敏锐,观察更入木三分.
二、动态几何问题
动态几何问题,是探究几何图形(如点、直线、三角形、四边形)运动变化过程中与图形相关的某些量(如角度、线段、周长、面积及相关的关系)的变化或其中存在的函数关系的一类开放性题目.解答这类问题的关键是“动中求静”,并灵活运用有关数学知识加以解决.这类问题形式多样,难度较大,在中考中往往以压轴题的身份出现.
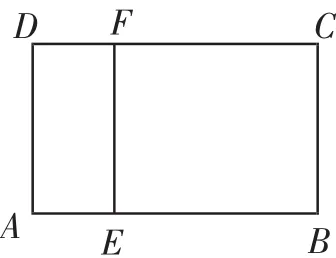
图4

图5
例2如图4,矩形ABCD的边AB上,有一个动点E从A出发,沿AB→BC方向移动,一旦点E与点C重合,马上停止移动,过点E作FE⊥AE,交CD于F点,令点E移动路程的长度为x,FC=y,图5所表示的是y与x的函数关系的大致图像,当点E在BC上移动时,FC的最大长度是,那么矩形ABCD的面积是( ).
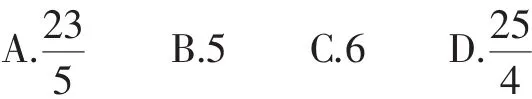
解析:点E在BC上时,如图6,由∠EFC与∠AEB互余,∠FEC与 ∠EFC互 余 ,得∠CFE与∠AEB相等.
在△CFE和△BEA中,∠CFE=∠AEB,∠C=∠B=90°,所以△CFE △BEA.

图6
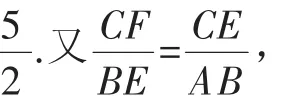
评析:几何与代数的综合,体现了数形结合思想,历来是中考命题热点.本题不仅考查二次函数的图像与性质,同时考查相似三角形的判定和性质及矩形面积的计算,试题体现了逻辑推理与数学运算的核心素养.
三、类比探究问题
类比是伟大的引路人.类比思想是数学探究中经常用到的思想方法,类比探究,也成为中考命题的重要考点.在中考试题中,类比探究问题的知识跨越大,综合性较强,命题立意高,题意新颖,构思精巧,追求考题深度和难度.解答这类问题,考生必须有扎实的基本功,以及善于思考、乐于钻研的创新能力.应在平时加强综合能力训练,只有这样,才能以不变应万变,才能在中考中顺利攻克这类问题.
例3(1)刘刚同学特别喜欢数学,尤其喜欢钻研数学竞赛题,下面这道题请你也不妨来做做看:
假如已知圆内接六边形ABCDEF的六条边长分别为3个3和3个5,那么该六边形ABCDEF的面积你会求吗?
刘刚同学采用“同圆中相等的弦所对的圆心角相等”,把六边形进行分割重组,得到图9.能求出六边形ABCDEF的面积等于______.
(2)继续类比探究:假如圆内接八边形各边长度分别为4个2和4个3.试求这个八边形的面积.同学们,请你仿照刘刚同学的做法,求出这个八边形的面积.

图7
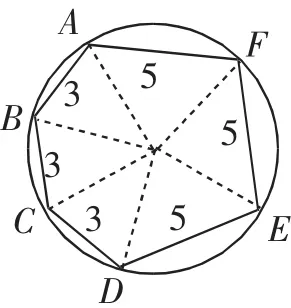
图8
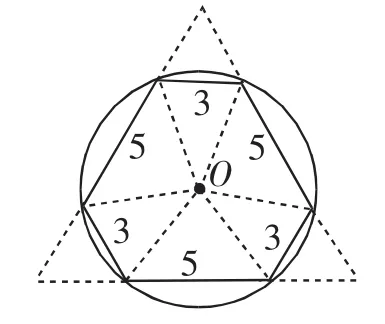
图9
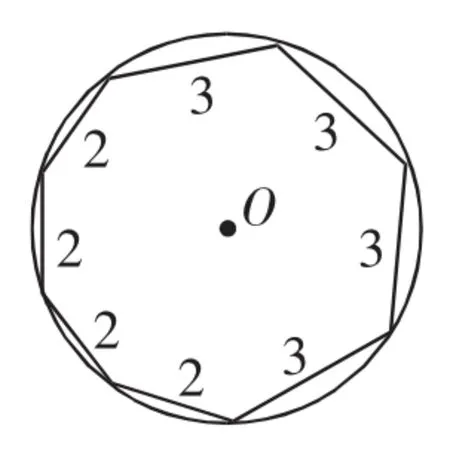
图10
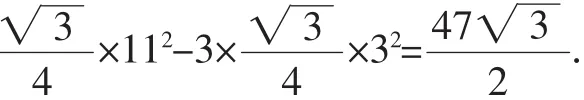
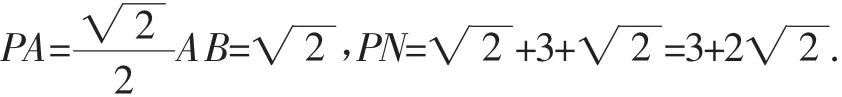
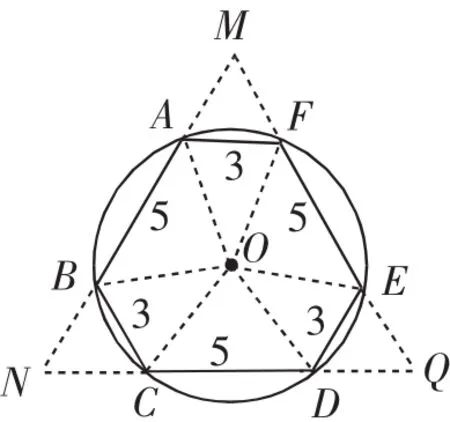
图11
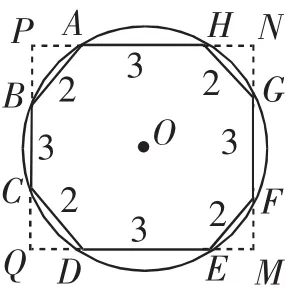
图12
评析:本题主要考查几何图形的旋转变换和类比推理能力,考查三角形面积的计算.本题新颖独特,又具有一定的思维量,能全面考查考生分析问题与解决问题的能力,区分度较强.
几何探究题年年变化,年年出新.在平时复习时,我们应抓住典型问题,深入研究,这样我们才能悟出其中的方法,才可以不变应万变.W

