高考数学最值问题的求解方法*

☉内江师范学院数学与信息科学学院 胡生兵

☉内江师范学院数学与信息科学学院 赵思林

最值问题是高考的热点和难点问题.历年的高考试题中都包含着大量的最值问题，如函数最值、数列最值、几何最值等问题.最值问题的解决有利于培养学生发现问题、提出问题、分析问题和解决问题的能力，同时也是培养学生数学核心素养的好素材.最值问题的求解方法有很多，如配方法、判别式法、三角代换法、不等式法、函数单调性法、向量极化恒等式法等，下面通过一些典型问题来说明这些方法的应用.

一、配方法

配方法主要是运用于二次函数或者可以转化为二次函数的函数最值问题中.在解题过程中一定要注意自变量的取值范围.

例1已知函数y=（ex-2）2+（e-x-2）2，求函数y的最小值.

解：由y=（ex-2）2+（e-x-2）2去括号可得y=e2x-4ex+4+e-2x-4e-x+4=（e2x+e-2x+2）-4（ex+e-x）+6=（ex+e-x）2-4（ex+e-x）+6.

令t=ex+e-x，则t≥2.所以y=t2-4t+6=（t-2）2+2，从而ymin=2.

点评：解决此问题的关键在于换元和配方.

二、判别式法

判别式法是根据已知条件和求解目标来构造一个一元二次方程，根据构造过程可知，二次方程有根，所以判别式大于等于零，进而使问题获解.

例2已知实数a，b，c成等比数列，a+6，b+2，c+1成等差数列，则b的最大值为______.

解：因为实数a，b，c成等比数列，所以b2=ac.

因为a+6，b+2，c+1成等差数列，所以2（b+2）=a+6+c+1，化简得2b-3=a+c.

所以a，c是方程x2-（2b-3）x+b2=0. 所以Δ=（3-2b）2-

点评：根据已知条件，得到a+c，ac的值，从而联想到根与系数的关系，进而想到构造一元二次方程.此题有利于培养学生的观察、联想、猜想等数学思维品质.

三、三角代换法

三角代换法是运用三角函数进行换元，它是求解最值问题的常用方法.三角代换法主要是运用三角函数的有界性.这种方法可以减少运算量，从而降低问题难度.

例3（2018年全国卷Ⅲ文科第8题）直线x+y+2=0分别与x轴，y轴交于A，B两点，点P在圆（x-2）2+y2=2上，则△ABP面积的取值范围是（ ）.

点评：取值范围问题的实质就是求最大值和最小值.因为AB长度固定，所以只与点P到直线的距离有关，而点P的轨迹为圆，所以选择三角换元，直接运用三角函数的有界性，使问题轻松获解.

四、不等式法

不等式主要是指基本不等式、几何不等式、算术平均值、柯西不等式等等.当“和”或“积”为定值时，常常运用基本不等式来处理.在运用的过程中，一定要检验能不能取等号.

例4（2018年江苏卷第13题）在△ABC中，角A，B，C所对的边分别为a，b，c，∠ABC=120°，∠ABC的平分线交AC于点D，且BD=1，则4a+c的最小值为______.

解：因为S△ABC=S△ABD+S△BDC，

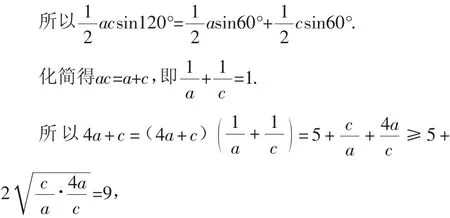
所以4a+c的最小值为9.

五、函数单调性法

函数的单调性有着广泛的运用，可以用来求方程的根、函数的零点、解不等式、求最值等等.函数的单调性是求解函数最值问题最基础的方法.

例5（2018年全国卷Ⅰ理科第16题）已知函数f（x）=2sinx+sin2x，则f（x）的最小值是______.

解 ：f ′（x）=2cosx+2cos2x=2cosx+2 （2cos2x-1）=

点评：此方法就是从函数的视角来看待这个问题，体现了求函数最值的通法.此方法的关键在于因式分解.此处的因式分解考查了学生敏锐的观察力以及丰富的解题经验.

六、向量极化恒等式法

在解决有关向量的最值问题时，当已知条件包含中点时，绝大可能是使用极化恒等式.通过极化恒等式不仅可以减少未知量的个数，而且可以将动态问题转化为静态问题，同时还可以得到一个恒等式，从而避免讨论参数，降低问题难度.

例6（2018年天津卷理第8题）如图1，在平面四边形ABCD中，AB⊥BC，AD⊥CD，∠BAD=120°，AB=AD=1.若点E为边CD上的动点，则的最小值为（ ）.

图1

图2

解：如图2，取AB的中点F，则有

如图2，过点F作FM⊥DC，垂足为M，过点B作BN⊥DC，垂足为N，连结AC.

又因为在梯形ABND中，AD=1，FM为梯形的中位线，所以