基本不等式复习课三步曲
☉江苏省宜兴市阳羡高级中学 孙 玲
基本不等式在高考中属于C级要求,即要求学生熟练掌握,并能灵活应用.而在新授课时,如何灵活运用基本不等式解决有关问题,一直是学生的弱点与难点.因此,在基本不等式的复习课上,教师应该引导学生克服弱点与难点,并温故知新.为此,笔者设计了基本不等式复习课三步曲,供参考与斧正.
一、引导学生梳理知识,并完成基础训练
作为复习课,这一步必不可少,既起到“温故”的作用,又起到承上启下的作用.
(一)知识梳理
1.几个特殊的平均值
2.基本不等式
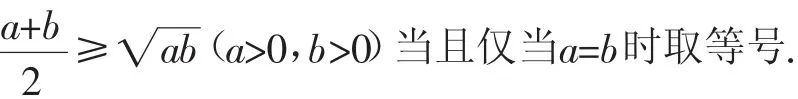
3.不等式的几个变形

4.利用基本不等式求最值问题
已知x>0,y>0,(1)如果积xy是定值p,那么当且仅当x=y时,x+y有最小值是;(简记:积定和最小)(2)如果和x+y是定值p,那么当且仅当x=y时,xy有最大值是(简记:和定积最大)
应用注意点:一正,两个未知数为正数;二定,两个未知数的积定或和定;三相等,当且仅当两个未知数(或整体)相等时取等号,注意定义域.
5.证明基本不等式的方法有分析法、综合法和比较法
点评:复习课必须围绕课题梳理知识点,梳理应做到全面且重要,应提取课本精华并加以深化.如果用不等式链来高度概括a+b,ab,a2+b2三个量之间的不等关系会更加简洁明了.
(二)基础训练
1.已知a,b∈R,a+b=1,则a2+b2的最小值为______.
4.用长为4a铁丝围成一个矩形,则矩形的面积最大值是______.
5.下列函数中,最小值是4的有______个.

点评:以上题目涵盖了基本不等式的简单运用、实际应用和运用基本不等式求最值时的条件,达到了夯实基本概念和基本知识的目的,而且大部分学生都能顺利解决.
二、通过例题引导学生进一步明确并掌握基本不等式的应用
例题讲解一直是复习课的主旋律,因此例题的选择十分重要,因为它是引导学生掌握知识并形成能力的载体,所以例题的选择必须典型,同时要注意进行适当变式,以培养学生思维的灵活性.
1.证明不等式
例1(1)已知a,b,c均为实数,求证:a2+b2+c2≥ab+bc+ac;
变式1:已知a,b,c是不全相等的正数,求证
变式2:已知a,b,c是不全相等的正数,求证:lg
变式3:已知a>b>c,求证
点评:学会从不等式的特征分析,巧用基本不等式进行不等式的证明.注意轮换对称式的识别,并应用叠加或叠乘法解决问题,同时学会拆、凑等技巧来构建基本不等式.
2.求最值或取值范围
例2 已知正实数a,b满足ab=a+b+3,
(1)求a+b的最小值;(2)求ab的最小值;(3)求2a+b的取值范围.
变式4:已知实数x,y满足4x2+y2+xy=1,求2x+y的最大值.
点评:解决双元代数式最值的两条解题途径:一是把a+b和ab看作两个量,利用基本不等式及其变形构建不等式,通过等式消元,解不等式即可求解;二是把a、b看作两个量,通过等式消元,构建函数关系,再利用基本不等式或函数的单调性解决问题,同时注意消元的等价性.
3.在实际问题中的应用
某村计划建造一个室内面积为800m2的矩形蔬菜温室.在温室内,沿左、右两侧与后侧内墙各保留1m宽的通道,沿前侧内墙保留3m宽的空地.当矩形温室的长、宽各为多少时,蔬菜的种植面积最大?最大种植面积是多少?
点评:学会根据题意列出相应的等量关系,并通过消元或构建不等式求最值.
图1
三、引导学生了解基本不等式的高考动态
学习的目的虽然不是为了高考,但对于每一位学生来说,高考不可回避.在复习课上,教师让学生了解基本不等式的高考命题趋势,或高考真题回顾,能激发学生的求知欲,并能让学生从“温故”走向“知新”.
1.最新考纲
(1)了解基本不等式的证明过程;
(2)会用基本不等式解决简单的最大(小)值问题.
2.高考命题趋势
在高考中,对基本不等式的考查一般不以知识点的形式出现,而是考查它的“工具性”,即利用基本不等式解决有关最值问题与不等式问题,其常与其他知识综合在同一考题中,以此来考查不等式应用的综合性与灵活性.
3.高考真题
例3(2018年天津高考)已知a,b∈R,且a-3b+6=0,则的最小值为______.
解析:由a,b∈R,且a-3b+6=0得,3b=a+6,

上述解法采用了代入消元法,把两元最值问题转化为一元最值问题,然后再利用基本不等式求最值,这是求多元最值问题最基本的方法之一.
变式5:(2018年江苏卷)在△ABC中,角A,B,C所对的边分别为a,b,c,∠ABC=120°,∠ABC的平分线交AC于点D,且BD=1,则4a+c的最小值为______.
解析:如图2,因为∠ABC=120°,且BD为∠ABC的平分线,
所以∠ABD=∠CBD=60°.
又因为角A,B,C所对的边分别为a,b,c,且BD=1,
由S△ABC=S△BDC+S△ABD得,


图2
故答案为:9.
点评:高考真题体现了高考命题的方向,不仅可以让学生感受基本不等式的高考要求,又能感受基本不等式应用中体现的数学思想,进而从高考的角度去理解基本不等式.
常言道:学无定法,教无定法.但有规律可循.笔者认为复习课也应遵循学生的认知规律,尤其是在高考的一

