妙用图像规律 巧解函数问题
☉江苏省苏州市苏州高新区第一中学 陈 瑜
函数是高中数学的核心内容,对于绝大多数学生而言,函数的学习是具有较大难度的,再加上函数部分涉及的知识点较多,因此有部分学生会存在畏惧心理.在考试中,函数试题变式繁多,涉及许多函数的性质及变化,在很多的压轴题中,函数方法或思想是常见的考点,如果学生的函数学习基础不扎实,对函数方法掌握得不到位,那么在分析、解答这些问题时就会遇到困难,甚至是毫无思路.借助函数图像,学生能够理解函数的各种性质以及变化规律,是辅助学生学习、答题的工具.
一、函数图像的教学意义
(一)理解函数概念
函数的定义为:对于定义域中任何一个自变量,值域中都有唯一确定的值与之对应.学生对于这个概念缺乏直观的认知,理解起来比较困难.借助函数图像,学生就会发现,如果x在定义域内任意取一个值,表示的是x=m这一条直线与函数值域曲线至多有一个交点,如果出现了2个甚至多个交点,那么就不符合函数的定义.
(二)描述函数性质
函数图像的变化规律、周期性、对称性可以直观地反映函数的单调性、周期性等性质,学生通过观察图像,可以更加直观地感受到函数的这些性质.在教材中,函数性质的教学也都是借助函数图像进行的.
(三)辅助解题
在解决函数问题时,图像是一个很好的辅助手段,可以将函数的变化特征、性质等直观地反映出来,在填空题的解决过程中,借助函数图像可以省去复杂的推算过程,既化繁为简,提高了正确率,又节省了答题时间.
二、函数图像解题技巧
(一)巧解小题,节省时间
在考试中,时间是有限的,数学学科题目多,难度大,因此在日常的训练中教师要引导学生发现、总结常见题型的最优解答方法,通过简便的解题方法来快速、准确地解决问题,尤其是最前面的填空题,为难度大、分值高、解题步骤要求高的解答题争取更多的时间.
在解答填空题时,我们经常会遇到比较复杂的题目.这时,我们就需要选用最为简便的解答方式,因为填空题不要求书写过程,答案正确就能拿分,所以要避免在这一题型中花费大量的时间,因小失大.具体来说,特殊值法、图像法都是可以简化解答过程的方法,需要我们转换思维,将题目的有用信息提炼出来,尽可能地结合函数图像快速获解.
例1曲线与直线l:y=k(x-2)+4有2个不同的交点,则实数k的取值范围为______.
解答:由图1可知,当直线l在AM和AN之间时,和半圆存在两个不同的交点.不难求解,直线AM的斜率此时直线与半圆相切,有且仅有1个交点,是临界状态;直线AN的斜率为因此,如果直线l和半圆有两个不同的交点,那么直线l的斜率的取值范围为],即k的取值范围为
分析:这是一道常见的函数问题,对于这类题,从代数角度直接运算是很困难的,在时间有限的考试中几乎不可能准确求解.因此,我们就需要结合函数图像进行分析与解答.显然,曲线y的形状为一个半圆,直线l:y=k(x-2)+4的解析式不确定,但是过一固定点(2,4).通过以上分析,我们就可以大致绘制出题干信息中所描述的图形关系,如图1所示.
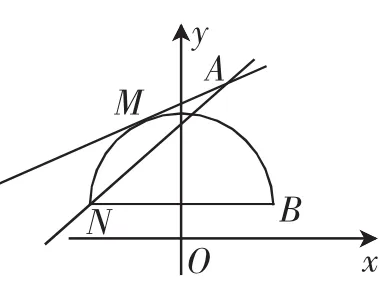
图1
(二)绘制图像,分类讨论
在解决一些函数问题时,从题干信息我们并不能确定解题思路,需要深入分析.比如,在判断函数图像时,对于给定的函数关系式,我们不能确定唯一解,对于其他潜在的答案又不能直接否定,这时我们就需要借助函数图像,结合函数性质来分类讨论.
例2如果函k不为0)以及函数y=k(1-x)在同一个图中,请绘制出符合条件的函数图像.
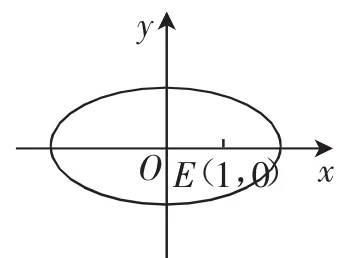
图3
分析:面对这样的一种函数图像问题,首先要做的不是去判断图像,而是去分析题干信息中的两个函数解析式.y=k(1-x)=-kx+k,这是一个一次函数表达式,如果想要确定函数图像就需要对k的取值情况进行讨论.因为这个问题中两个函数的k值是统一的,因此我们的解题思路就以该函数为主,以这一函数为辅,通过对前一个函数的图像分析就可以确定这两个函数图像的整体状态,不仅节约了时间,简化了解答过程,而且提高了解答的正确率.
解答:对于函数y=-kx+k而言,如果k>0,那么函数图像必定经过第一、第二、第四象限,令x=0,y=k>0,则函数与y轴的正半轴相交.函数的图像经过第一、第三象限;如果k<0,那么函数图像一定经过第一、第三、第四象限,令x=0,y=k<0,则函数与y轴的负半轴相交.函数的图像经过第二、第四象限.根据以上分析,可以确定两种情况符合题目要求,如图2所示.

图2
(三)数形结合,值域求解
在高中函数问题中,值域求解是常考题型,形式多样,常与解析几何、向量等考题共同出现.如果从代数角度着手求解,那么计算量会很大,也很难求出正确结果.如果结合函数图像,那么值域的求解就会简便很多.
例3已知A,B为椭圆y2=1上的两个动点,点E的坐标为(1,0),如果满足EA与EB垂直,试求向量数量积的范围.
分析:这道题表面上是解析几何以及向量问题,但是设问为向量积的取值范围问题,我们就需要对题目进行转化,将其变成函数值域问题.
解答:假设点A的坐标为(a,b).由题目已知条件可知,EA与EB垂直,那么向量又因为A点在椭圆上,满足,其中a的取值范围为[-2,2],所以可知,问题就转化成了求解关于a的二次函数在区间[-2,2]上的值域,不难求解出的取值
三、结语
函数图像的应用很广泛,除了本文所述之外,在求解方程近似解、确定函数值域等方面也有重要的应用.借助函数图像解决函数问题的实质就是数形结合的思想方法.要想在考试中能够熟练应用这种方法,教师就需要在初等函数的教学过程中训练学生的数形结合能力,归纳总结出常见函数图像问题的解题思路,让学生在遇到这类考题时能从容应对.

