优选问题,挖掘本质
——基于深度思维的数学教学
☉四川省德阳外国语学校 顾有良
一、问题的提出
美国数学家哈尔莫斯说过:“问题是数学的心脏.”而思维源于问题,数学教学是一个数学思维活动的切入、分析、归纳与总结的过程,集中体现为提出问题、分析问题与解决问题的过程.因此数学教学必须从问题开始,以问题为载体,以问题的解决为中心,引发和指导学生的思维活动,真正调动起学生的全面思维,激发学生的深度思维,使其充分参与并揭示相关知识的发生过程、方法的形成过程以及问题的解决过程.这样的数学教学一定能充分体验到数学知识的美妙,培养出数学素养,步入数学幽境,真正使学生在数学教学的过程中优学、好学、乐学.
在数学教学过程中,针对数学课本、配套练习、课后练习、模拟试题、各类考试试题以及历年高考真题等众多的数学习题,以及各层面各类型的考试及其对应的试题,教师讲不过来,学生也做不过来,那么在课堂上优选问题并展开讨论,从而达到深度思维才是有效的课堂.
二、问题的分析
如何优选数学问题作为数学教学的媒介,是教师必须考虑的重点问题,特别是在高三复习阶段,如何在较短的时间内进行有效复习与全面提升?优选问题就显得更为重要.优选问题可以有效地节约时间,有针对性地进行讲解与训练,还可以在一定程度上保障深度思维的展开,从而得以真正有效地掌握知识,提升能力.
当然,作为数学教学过程中优选出来的典型问题,必须要具备典型性、代表性、知识性以及拓展性等相关的性质,通过讲评优选出来的问题,既可以讲清所要掌握的知识点,又可以与已有的知识加以有效联系与复习,在一定程度上还可以进一步拓展与提升,从而真正达到深度思维,形成学生固定的知识体系与思维习惯,这才是最终的目的.
那么如何有选择性地选取相应的数学问题,并进行针对性的数学教学,深化数学知识,拓展深度思维呢?
三、问题的解决
其实,可以进行有效的深度思维并优选出相应的数学问题主要存在于三个地方:课本中的例题与习题、各地有代表性的模拟题、历年的高考真题等.当然,在具体的教学过程中,要有意识地加以积累,并有针对性地加以总结、归类、反思、更新.
1.细选课本例题(习题)
数学教材中各部分的例(习)题具有典型性、代表性、示范性、迁移性与拓展性等特点,是几代数学专家、学者集体智慧的结晶,历经考验.课本上一些例(习)题,看似平淡无奇,但都隐藏着深远的背景,闪烁着智慧的光芒,有着意想不到的功能.因此通过细选这部分数学问题,在充分讲解并深刻理解的基础上,还要进一步拓展与提升,才能真正做到深化思维.
普通高中课程标准实验教科书《数学·选修2-3·A版》(人民教育出版社,2009年4月第3版)第35页探究与发现:“杨辉三角”中的一些秘密.
问题1:对于“杨辉三角”,探究与发现中给出4点规律.
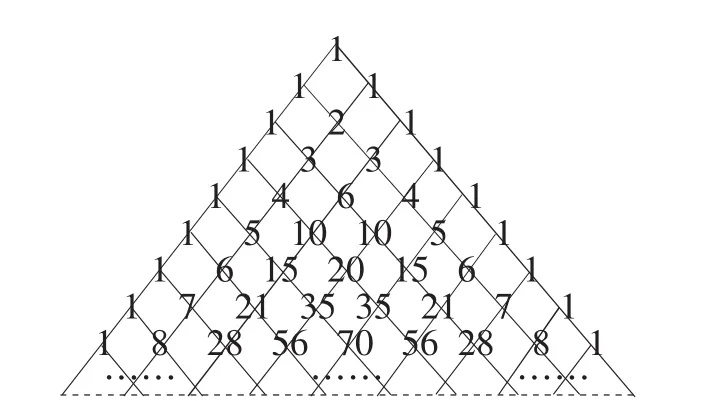
图1
通过进一步拓展与探究,还能发现什么规律?这才是深度思维的进一步拓展与应用.
通过分析可以进一步归纳出众多的规律,比如:(1)在杨辉三角中,第2n-1(n∈N)行的整行均为奇数;(2)在杨辉三角中,若第p行(n∈N)除1外,p整除其余的所有整数,则行数p是质数(素数);(3)在杨辉三角中,同一行中存在相邻的三个数成等差数列所满足的条件是:且k≥3)等等.
其实,借助“杨辉三角”,通过三角形数表形式,还可以拓展到其他类型的数表形式,其实质都是二项式定理、数列、函数、推理与证明等相关的数学知识的综合与应用,充分体现了高考大纲对数学文化的展示以及创新应用,从而起到扩大知识面,提升能力,深化思维的目的.
2.优选高考模拟题
高考模拟题是一线教师与一线数学教研员们在一线教学过程中的体会、反思与总结,其中包括对课本知识的领会、高考大纲的理解、高考命题的剖析以及学生情况的反馈等众多方面,具有极高的应用性.当然对高考模拟题要有针对性地选取,应选取相应教学时段所对应的问题,并加以合理应用与深化思维.
问题2:(2019届江苏省靖江高级中学高三12月月考)已知圆O:x2+y2=1,定点A(3,0),过A点的直线l与圆O相交于B,C两点,B,C两点均在x轴上方,如图2,若OC平分∠AOB,则直线l的斜率为______.

图2
本题以解析几何中的圆为问题背景,通过直线与圆的位置关系的建立,结合角平分线条件的介入,最终落到直线斜率的求解上.巧妙地把解析几何、平面几何加以交汇,把圆的方程、直线的方程、直线的斜率、角平分线等相关知识加以链接,进而达到知识交汇与能力拓展的目的.
常规思维方式——(交点法)结合角平分线定理的转化得到|AC|=3|BC|,过点C作CD∥BO交x轴于点D,结合平行性质得到点C所在的圆并结合点C在圆x2+y2=1上确定点C的坐标,再利用直线的斜率公式求解即可.
解析:由于OC平分∠AOB,所以由角平分线定理可得,则知|AC|=3|BC|.


图3
通过深度思维,可以与三角形面积加以结合,利用三角形面积转化法来处理;也可以与角平分线定理加以结合,利用角平分线定理转化法来处理;还可以直接回归到坐标法,结合平面向量等相关知识来处理;又可以通过题目条件进行深度分析,并借助三角参数,利用三角参数法来巧妙解决.
优选高考模拟题,从一个简单的基本问题入手,把解析几何问题与平面几何、平面向量、三角函数等相关知识加以有效整合,既拓广了思维以及应用,又提升了能力,培养了素养.
四、感悟与反思
我们关注数学教学中的深度思维,本质上就是关注学生数学知识的构建效率与效度,这与数学课程标准这一根本目的完全吻合,也充分体现了数学核心素养.
因此,打造数学教学的深度思维,需要清晰明确的学习目的、起点与终点,通过数学问题的驱动,架起新旧知识间的桥梁,使得数学思维真正走上“高速公路”,达到深度思维,往广处、深处等各个方面渗透、拓展.坚持这样的数学教学,有意识渗透深度思维,那么有深度的数学课堂与数学教学就有可能实现,学生的数学知识有可能得以掌握,学生的数学核心素养有可能得以养成.

