关注探究过程、结果、经验积累的实践探索
☉江苏省仪征市第二中学 俞仁宗
“试卷评析”是每个数学教师都必须完成的一个教学环节,帮助学生总结得失并根据学生的错误进行寻根思底是试卷评析最基本的任务,除此以外,教师还应在试题研析的基础上进行专题的开发,使学生能够在有意义的试题拓展和延伸中得到能力的发展.
以下面的典型试题为例进行试题评析如下:
题目:若不等式|2x-a|+|3x-2a|≥a2对任意实数x恒成立,则满足条件的实数a组成的集合为_____.
测试评析:
考查统计:528名考生中答对的仅有31人,得分率在6%以下.
错因分析:①时间紧迫而放弃此题的解答;②存在根据绝对值的意义求解的思路,但最终在系数问题上止步而无法求解;③分类讨论时觉得烦琐而欠缺条理致使解题半途而废.
教学反思:①教学趋于常态,对归纳、提炼、经验积累等环节较为忽略;②教学中未对学生进行探究的策略引导,致使学生的思维在低层次的训练中未能达到应有的深度;③对“通性通法”过于重视而忽略了“技巧”训练.
评析教学预设:①从最简单的入手并逐步深入,引导学生在对“区间套”的探索与思考中获得“最优点”;②引导学生在此题的评析、探索与反思中获得对此类题目的解题领悟,并因此获得经验的积累和持久的掌握.
教学过程:
教师:研究|x-1|+|x-3|的最小值有哪些方法呢?
学生2:借助数轴来研究也行得通,如图1,当x2∈[1,3]时,|x2-1|+|x2-3|是最小的.

图1
教师:大家能对其中的一般性结论进行总结吗?
学生3:(|x-a|+|x-b|)min=|a-b|.
教师:不错,事实上,闭区间[1,3]上所有的点都能令其取得最小值.那么如果我们将绝对值增加至3个,如|x-1|+|x-2|+|x-5|,是否还能得出一个结论呢?
学生讨论……
学生4:观察发现|x-1|+|x-2|+|x-5|=|x-1|+|x-5|+|x-2|,经过这样的调整,我们容易得出(|x-1|+|x-5|)min=4,2也正好在区间[1,5]之内,若把x=2代入即可获得最小值4.
学生鼓掌.
教师:若是4个呢?比如|x-m1|+|x-m2|+|x-m3|+|x-m4|?
学生5:从图2的观察中可以得出,闭区间[m2,m3]上的点既能令|x-m2|+|x-m3|取得最小值,同时也能令|x-m1|+|x-m4|最小.因此可得出以下结论:若是2n(n∈N*)个绝对值相加,当x=mn或x=mn+1时,均能取得最小值.
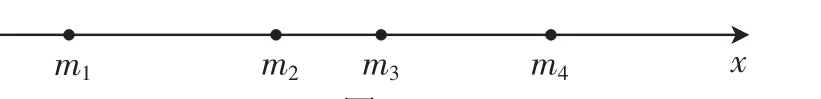
图2
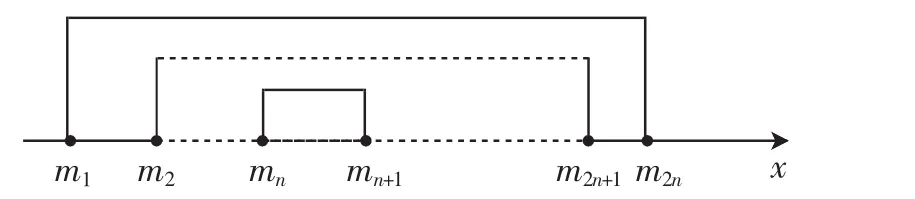
图3
学生6:可以发现x∈[mn,mn+1]时能取得最小值.
教师:若是奇数个绝对值相加又会怎样?
教师:还有其他一般性的结论吗?
学生进入再次的探究中…
学生8:从分析中可以得出,取闭区间上的点和取中间点均能归结为“特征点”问题,也就是说对于K个绝对值相加,第即为需要的“特征点”.
教师:非常好!我们在线性规划问题中曾经探寻过“尖点”来解决最值问题,这一“以点带面”的经典范例也是处理数学问题的重要举措.那么,绝对值前面的系数不是“1”的问题又应该怎样解决呢?例如:求3|x-1|+5|x-3|的最小值.
学生9:可以将3|x-1|+5|x-3|转化成3(|x-1|+|x-3|)+2|x-3|,从前面看,只要x∈[1,3],|x-1|+|x-3|总有最小值,|x-3|最小能令整个式子取得最小值,则令x=3即可,其最小值是2.
学生10:化归到上面的研究中也是可行的,将3|x-1|+5|x-3|拆成|x-1|+|x-1|+|x-1|+|x-3|+|x-3|+|x-3|+|x-3|+|x-3|,将前面3个“1”看成不同的点,原问题即转化成了“8个点”的问题,中间一个即为|x-3|,把3代入就解决问题了.
学生鼓掌.
教师:大家再来看看以下两个式子,大家能否以最快的速度求出其最小值呢?
①6|x-1|+5|x-2|+17|x-3|;
②|x+1|+2|x+2|+|x-1|+4|x-7|.
学生11:①(6|x-1|+5|x-2|+17|x-3|)min=6|3-1|+5|3-2|+17|3-3|=17.
学生12:②(|x+1|+2|x+2|+|x-1|+5|x-7|)min=|7+1|+2|7+2|+|7-1|+5|7-7|=32.
教师:大家在探究的过程中有什么体会?
学生13:我在探究时感受到了“重心”的味道.
教师:为什么呢?
学生13:我感觉在系数不同的情况下,系数较大能占据较大的主动权.
教师:太棒了!其他同学可有什么看法?
学生14:我的看法跟他不同,对于6|x-1|+5|x-2|+17|x-3|,三点的“重心”应该为:如果以2.5来代入运算,结果为20,还是比17大啊.
教师:大家能对其中的缘由进行解释吗?
学生15:“区间套”的最小子区间与“重心”并不一定是同一回事,略有“倾斜”的现象也不影响我们的判断.
教师:那么,在“区间套”和“重心”这两者之间,我们应看好哪个呢?
学生15:区间套.
教师:那么我最后作一下总结吧.
学生16:如果有2n-1(n∈N*)个绝对值相加,最中间的一个即为“特征点”;如果有2n个绝对值相加,将区域[mn,mn+1]的右端点作为“特征点”.
学生17:对于k1|x-m1|+k2|x-m2|+…+kn|x-mn|,首先求出k1+k2+…+kn,假如k1+k2+…+kn是奇数,选择第个点代入运算;假如k1+k2+…+kn是偶数,选择第+1个点代入运算.

学生19:绝对值内x的系数不是1又该怎么办呢?
学生20:将系数从绝对值里提出来就没有问题了.
教师:这一探究正好是华罗庚教授的一个观点的印证,我们在解决复杂问题时要能够“退”并“退”到最原始且又不失重要性的地方,这种足够的“退”也是解决数学问题的一个诀窍.正确的“退”有利于我们探寻问题的出处,不仅如此,合理的“退”还能对命题者的心理与意图进行准确的揣摩并因此在解题中顺利搭建思维台阶,最终发现题目中的基本原理而令问题顺利得解.大家要懂得复杂源于简单、抽象源于具体,并因此在解决问题时对问题进行拆解、类比、图示、列举并最终顺利获得解题的突破.
(多媒体投影)
解:由题意可得|2x-a|+|3x-2a|≥a2恒成立⇔(|2x-a|+|3x-2a|)min≥a2.问题立即转化成了求(|2x-a|+|3x-2a|)min问题.由
大家在上述探究之后还会一五一十地进行分类讨论吗?大家对于此题有没有感觉这甚至是一条心算口答题呢?我相信很多同学都能脱口而出,给一答案.W

