论教材中向量习题编排之“用心良苦”

☉江苏省连云港市海滨中学 宋丽萍

☉山东省济南市莱芜区雪野镇中心中学 张光发

《平面向量》是苏教版必修4第二章的内容，它不仅是高中数学中非常重要的知识点，也是我们解决诸多数学问题时常用的数学工具之一.平面向量是每年高考的必考内容，它的考查内容主要集中于向量的线性表示、向量的坐标运算以及向量的数量积这几个方面，且在选择题、填空题和解答题中都有出现过，难度不算大，以基础题和中档题为主，这类考题应该是考生比较容易得分的题目，因此，在平时的学习过程中，我们要认真研读教材，弄清教材编写者的意图，只有对一类问题穷追不舍、举一反三，才能在考试时做到“万无一失”.本文就和大家一起来体会教材在处理向量的线性表示这一基本问题时的“用心良苦”.

【教材原题1】教材第69页练习题第8题：如图1，在△OAB中，C是AB的中点，设

【教材解读】这个练习题安排在向量的数乘这一小节后面，我想编者的意图应该是希望学生可以借助于向量的数乘的知识来表示并加深对向量的数乘的理解，因此我们可以这样来解：

图1

其实，如果我们对题设条件中“C是AB的中点”仔细推敲，不难发现，可以借助这个中点将图形补成一个平行四边形，如图2所示，然后根据向量加法的平行四边形法则，

图2

【教材原题2】如图3，在任意四边形ABCD中，E、F分别是AD、BC的中点.求证

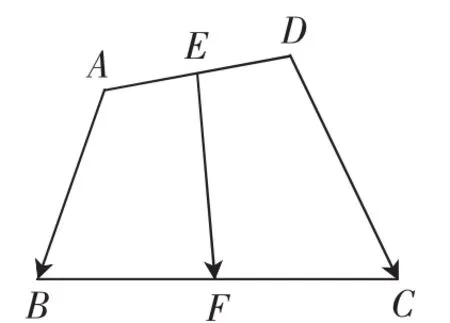
图3

图4

【教材解读】教材在此处安插本题，是对上面一道练习题的跟进，此题中隐含了原题1中的基本图形：连接EB、EC，如图4所示，根据原题1中的结论，我们就能迅速将向量，然后再由向量加法的三角形法则，得

另外，此题也是对教材第64页的思考“如果平面内有n个向量依次首尾连接组成一条封闭的折线，那么这n个向量的和是什么？”的实践，根据这个思考的结论：这n个向量的和是0，那么在封闭折线EFBA和封闭折线EFCD中，我们就有0，将两式相加，有2

以上两道教材原题都是从中点的角度来考虑，那么如果点不是中点，又该如何呢？教材在第71页练习题第7题中给出了这类情形：

【教材原题3】如图5，在△OAB中，C是AB上一点，且

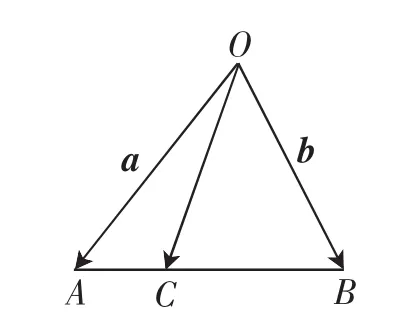
图5

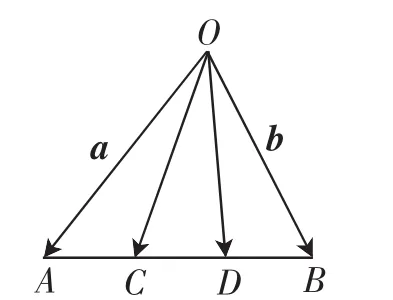
图6

【教材解读】本题是将教材原题1中的中点C修改为三等分点C，虽然图形稍有变化，但是仍然没有摆脱原题1中的基本图形的影响，我们可以取CB的中点D，构造向量OD，如图6所示，根据原题1中的基本图形和结论，在△OAD中，有而这种解法所涉及的图形在教材中又进一步加强，如教材第72页习题2.2中第10题：

【教材原题4】如图7，设点P、Q是线段AB的三等分点，若试用a，b表示向量

图7

这里我们就不再重复解答此题了，其解法和上题类似.

由此可以看到在教材原题1、原题3、原题4中，都是将点O与线段AB上某个定点之间所对应的向量用不共线的向量来表示，而且我们发现向量前的系数之和为常数1，在这里我们自然就要思考这样的问题：如果将点O与线段AB上的任意一点之间所对应的向量用不共线的向量来表示，是不是向量前的系数之和也为常数1呢？教材上考虑到了这一点，我们一起来看课本第71页例4：

【教材原题5】如图8，在△OAB中，C为直线AB上一点，■

图8

【教材解读】此题只要将中的向量用向量表示即可解出，即，整理得（.有没有发现向量前的系数相加为.从教材的编排顺序上，我们不难看出编者的“用心良苦”，由直线上的定点逐步过渡到直线上的动点，这就把定向量问题转变到动向量问题上来，这种潜在的转变，符合学生学习数学知识时的认知规律，体现了我们数学中的从熟悉到陌生、从特殊到一般的转化思想，至此，我们不难得出以下结论：

【结论】已知向量不共线，C为直线AB上任一点，若那么s+t=1.

上述结论是教材原题5的结论的延伸，其证明思路与方法和教材原题5类似，根据C为直线AB上任一点，得共线，再据平面向量共线定理，有而后用向量表示向量即可得到.读到这里，你会不会问：如果将向量用两个不共线的向量且s+t=1，那么A、B、C这三点是否共线呢？对于这个问题，我们教材在习题上也有了安排，请看教材第73页第15题：

【教材原题6】已知向量不共线，设实数，且满足a+b=1，求证：A，B，P三点共线.

【教材解读】此题主要还是为了增强学生对向量共线定理的理解，在此处证明三点共线，其本质就是向量共线，即证明以点A，B，P中的任意两点构成的具有公共点的两个向量共线，而向量共线的证明正是向量共线定理的作用所在，只要将b=1-a代入，化简即可得到共线得证，因此实施有效的转化是解决本题的关键.

向量的线性表示是向量的一种重要的表达形式，是向量部分的入门知识，也是后续学习向量知识的基石，因此我们在平时的学习中要对教材认真研读，细细品味，体会编者在教材中安排相关习题的意图，并适时加以小结、归纳，如果我们对每个知识板块都能如此用心，那么高中数学的学习就会变得顺畅起来.