高考题怎么改编（六）——数列篇

苏 玖

真题展现

（2018年北京卷第9题）设{an}是等差数列，且a1=3，a2+a5=36，则{an}的通项公式为__________.

思维延伸

由于等差数列对应的函数图象是直线上一群孤立的点，本题实质就是已知直线上两点坐标，求直线方程，于是就对应通项公式.（改编1）已知数列{an}满足an=pn+r（p，r为常数），a3=5，a7=13，求数列{an}的通项公式及其前n项和Sn.

本题的条件中没有说明数列{an}是等差数列，仅仅给出通项公式的一个代数式，于是利用待定系数法求出通项公式，再求其前n项和.如果已知数列的前n项和Sn的待定代数式，又怎样求其通项公式呢？

（改编2）已知数列{an}前n 项和Sn=f（n），f（n）=an2+bn+c（a，b，c为常数），若函数f（n）的图象经过点A（1，1），B（2，6），C（4，28）.

（1）求Sn以及an；

（2）求证：数列{an}为等差数列.

先利用待定系数法求出Sn的解析式，再利用an=Sn-Sn-1（n≥2），但不要忘记检验n=1，a1=S1的特殊情形，最后再利用等差数列定义证明.本题实质就是已知和式求通项公式，于是又可以改编为含有指数类和式问题：

（改编3）函数f（x）=c·ax+b（a＞0且a≠1，a为常数）的图象经过点A（1，1），B（2，3），设数列{an}的前n 项和为Sn，Sn=f（n）.求{an}的通项公式并判断{an}是否为等比数列.

本题的指数函数的底数是含有参数a的问题，而且首项为1，通项公式是分段函数类型，于是要对a进行讨论.当然也可以底数为定值，函数图象只过一个定点，于是又可以有：

（改编4）函数f（x）=c·2x+b的图象经过点A（1，1），数列{an}的前n 项和为Sn，Sn=f（n）.求{an}的通项公式并判断{an}是否为等比数列.

判断一个数列是否为等比数列，必须根据定义来确定，但对于含有参数的指数类数列问题，还是要利用分类讨论思想求解，要注意首项和公比均不为零.如果数列的前n项和满足一个分式类型的等式，又怎样研究呢？于是可以改编为：

（改编5）已知数列{an}的前n 项和为

（1）求Sn；

（2）求证：数列{an}为等差数列.

本题仍为已知和式研究通项公式，已知Sn之间的关系式，但是以分式形式给出的，于是要先求Sn，再求an.如果将等式右边分式中设置含有指数类型的项，可以改编为：

（改编6）数列{an}的前n项和为Sn，满足求an.前面几道题都是已知数列{an}的前n项和Sn，再求an.能否研究{Sn}的前n项的和呢？或者已知{Sn}的前n项和，再研究数列{an}呢？于是改编为：

（改编7）已知数列{an}的前n 项和为An，数列{An}的前n项和为Bn，

（1）求{Bn}的通项公式；

（2）求数列{an}的通项公式，并判断{an}是否为等比数列.

本题先通过和式求出Bn，再通过Bn求出和An，再通过An求an，最后再判断{an}是不是等比数列.

联想：（2018年浙江文科卷第20题）已知等比数列{an}的公比q＞1，且a3+a4+a5=28，a4+2是a3，a5的等差中项.数列{bn}满足b1=1，数列{（bn+1-bn）an}的前n项和为2n2+n.

（1）求q的值；

（2）求数列{bn}的通项公式.

点拨解析

真题展现：利用基本量法计算出公差d=6，于是通项公式为an=6n-3.

改编1解析：因为a3=5，a7=13，

因此an+1-an=2n+1-（2n-1）=2，由等差数列定义知，数列{an}是等差数列，

改编2解析：（1）由题可得，解得：所以Sn=f（n）=2n2-n.

①当n≥2时，an=Sn-Sn-1=（2n2-n）-[2（n-1）2-（n-1）]=4n-3；

②a1=S1=1也符合上式.所以an=4n-3.

（2）因为an+1-an=4，所以数列{an}为等差数列.

改编3解析：由题可知，所以

②n=1时，an=a1=S1=1.

（i）当a=2时，{an}是等比数列.

（ii）当a＞0且a≠1，2时，{an}不是等比数列.

改编4解析：由题可知，2c+b=1，所以b=1-2c，所以f（x）=c·2x+1-2c.

所以Sn=f（n）=c·2n+1-2c.

①当n≥2时，an=Sn-Sn-1=c（2n-2n-1）=c·2n-1；

②n=1时，an=a1=S1=1.

（i）当c=1时，an=2n-1，数列{an}是等比数列.

（ii）当c≠1时，数列{an}不是等比数列.

改编5解析：①-②得到：

所以Sn=n（n+1）.

（2）证明：①当n ≥2时，an=Sn-Sn-1=n（n+1）-（n-1）n=2n；

②a1=S1=2符合上式.

所以an=2n.

所以an+1-an=2，所以数列{an}为等差数列.

改编6解析：

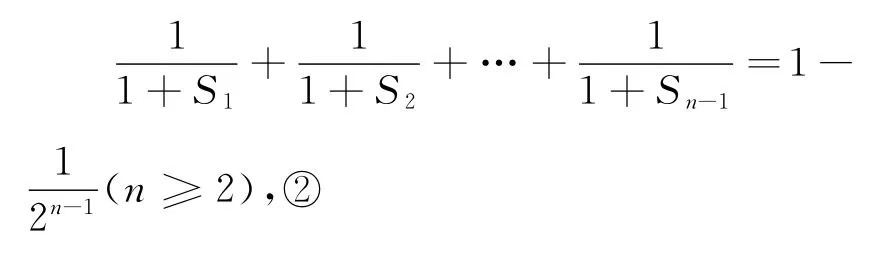
所以Sn=2n-1.

①当n≥2时，an=Sn-Sn-1=2n-2n-1=2n-1；

②n=1时，an=a1=S1=1.

所以an=2n-1.

改编7解析：（1）

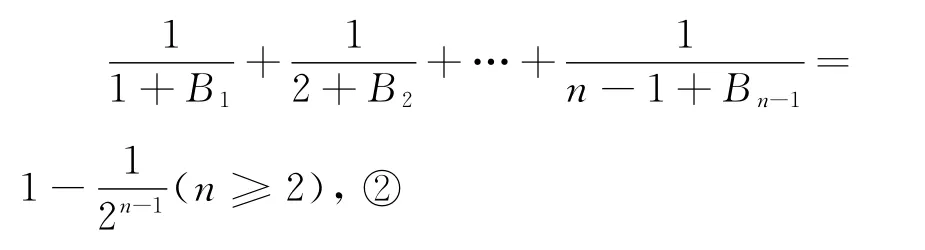
所以Bn=2n-n.

（2）①当n≥2时，An=Bn-Bn-1=2n-2n-1-1=2n-1-1；

②n=1时，A1=B1=1.

所以当n=1时，an=a1=A1=1；

当n=2时，an=a2=A2-A1=1-1=0；

当n≥3时，an=An-An-1=2n-2.

所以数列{an}不是等比数列.

联想题答案：（1）q=2；（2）bn=15-

回顾悟道

通过对一道简单高考题的分析和改编，可以看出，高考中对数列{an}问题的考查，主要是等差数列和等比数列，这既是重点也是热点；主要题型：一是求通项公式an，二是求数列的前n项和Sn，三是由Sn求an，主要利用四是数列与不等式整合的问题，要么证明不等式，要么求相关等式或不等式中的参数取值范围问题，但这类题型都是建立在前三种题型的基础上.因此改编高考题时，根据上述几点进行尝试.

题目：（2018年全国一卷文科第17题）已知数列{an}满足a1=1，nan+1=2（n+1）an，设

（1）求b1，b2，b3；

（2）判断数列{bn}是否为等比数列，并说明理由；

（3）求{an}的通项公式.

若将数列的递推关系如同前面讨论的改编题，用函数给出，你会改编吗？

（改编1）______________

（改编2）______________

原题答案：（1）b1=1，b2=2，b3=4.

（2）{bn}是首项为1，公比为2的等比数列.

（3）an=n·2n-1.

（改编1）已知函数f（x）=c·ax+b（a＞0且a≠1）的图象经过点A（1，1），B（2，2），C（4，8）.数列{an}，an=f（n），求{an}的通项公式.

解析：由题可得，解得：

所以an=f（n）=2n-1.

（改编2）已知函数f（x）=c·ax+b（a＞0且a≠1）的图象经过点A（1，1），B（2，2），C（4，8）.数列{an}的前n项和为Sn，Sn=f（n）.求{an}的通项公式并判断{an}是否为等比数列.

解析：由上题可知，f（x）=所以Sn=f（n）=2n-1.

①当n≥2时，an=Sn-Sn-1=2n-1-2n-2=2n-2；

②a1=S1=1.

所以an=

所以{an}不是等比数列.