牵牛要牵牛鼻子

上海 常文武

大家平日里解函数方程的题，常感无从下手.要想拨开迷雾，必须认清关键条件！那就是如标题所言，“牵牛要牵牛鼻子”.

来看一道题目：

显然第二个条件内涵更丰富.它虽然只是一个等式，但是可以一当十.因为只要取一些特殊的x，y 值代入它，就能得到函数在一些点上的特殊值.

可是取什么值呢？

一定要取到与第一个条件有关的值.让我们试试x=-1，y=0.效果不错啊，我们得到了

你会问，这一对特殊值怎么想到的啊？

无非是联系到第一个已知条件以及在第二个条件中，等式右边取y=0时会归于统一.

当然也可取其他途径.比如你也可能这么算：令x=y=0，得到4f（0）2=2f（0）.约去一个f（0）就得到同一个答案不过可得当心，万一约去的是个0呢？所以稳妥起见还是采用前一个方法.

现在让我们来扩大战果吧.

如果只令x=0，会怎样呢？这次我们得到f（y）=f（-y）.哈哈，原来这是个偶函数啊！则有f（1）=f（-1）=

仍然会有人问，为何想到令x=0呢？

其实这个想法也是很自然的，因为f（0）经过探索已知其值了嘛！

有了以上的摸索成果，我们可以向目标发起猛攻了！

如何能找到f（-2019）的值呢？

首先利用奇偶性，f（-2019）=f（2019）.接下来大概递推可以奏效吧？取y=-1，得到f（x）=f（x+1）+f（x-1）.这可以转化为一个递推式：f（x）-f（x-1）=f（x+1）.也就是说，前两项的差等于第三项.这样的话，我们总算看到了希望.满足以上递推式的f（x）在整格点上是个周期的数列：a，b，b-a，-a，-b，a-b，a，b，b-a，-a，-b，a-b，a，…，它的周期为6.所求的f（2019）=f（3）=-f（0）=

勤于思考的你又会问，怎么想到用递推来解题呢？

其实第二个条件中x+y和x-y都是在x的基础上平移了y.提示我们将y 取为-1来得出一个递推式.

问题解完了，可是我们仍然不知道函数f（x）的真面目.好奇的你也许还会问，这个f（x）可有解析式？

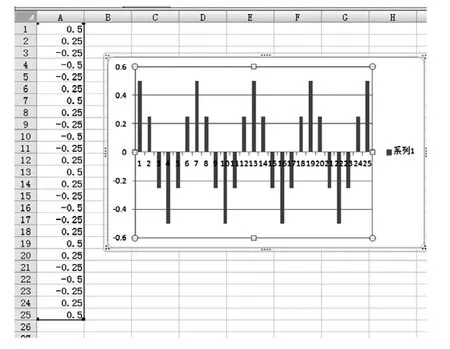
我们想到了数值模拟.请看上图，把一系列的f（n）在Excel中画出直方图，发现很像是余弦函数的图象.于是令f（x）=Acosωx，将f（0）=，周期T=6代入得：f（x）=

验证一下题设的两个条件，第一个显然对了.第二个条件：左边=右边.哈哈哈！我们貌似猜出了这个函数的庐山真面目！不过是否还有其他表现形式呢？我们还是不敢打包票，留给读者继续探索吧！

综上所述，我们发现尝试对问题进行求解的过程充满了艰辛.运气好的时候，我们可以势如破竹地前进.运气不好的时候，也就只能屡败屡试下去了.只有当你顺利牵到了题目的“牛鼻子”，题目才能迎刃而解.