简单直观≠正确

韦知辰

思考一道“无穷层指数塔”方程

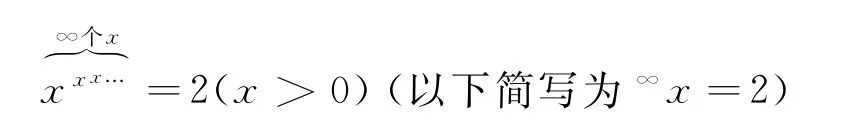
有的小伙伴看到这题可能会觉得没有思路.那么，先来看一道简单点的题目，把0.333…转化为分数.

因为0.333…×10=3.333…，

首先设A=0.333…，

即10A=3+A，

则

对于方程∞x=2也可以利用此方法.

首先，设∞x=A，

所以A=2.

注意到底数x的指数还是一个相同的“无穷层指数塔”，

于是有xA=2

所以x2=2，

最后x=.

那么，大家来试试手，解一下∞x=4，

设∞x=A，

所以A=4，

所以xA=4，

x4=4，

x=

一气呵成.等等，不知道大家有没有发现问题，这两道题的答案都是也就是说且也就是2=4.

这明显违背了我们的常识，问题到底出在哪？为什么会得出这么离奇的结论？

来看一下问题出在哪里，对于m 个x（x＞0）组成的指数塔方程，我们把方程左边（非常数项）记为mx，先取一些x的值，计算从1x到25x的值，探究它们的递变规律.

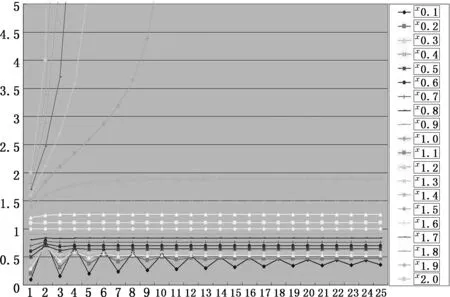
图1

可以发现，当x在一定范围的时候，随着m 从1增大到25，mx越来越接近一个值，而超过一个值之后，就会趋于无穷大.所以我猜想，在这两种情况中，存在一个x0，使得当x＞x0时，∞x为无穷大，而0＜x ≤x0时，∞x无限趋于一个定值N0.

假设∞x=N，由我们之前的算法可以得到

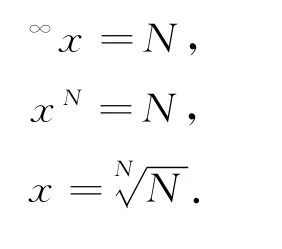
图2

可以发现F（N）确实是有上确界的，也就是x是有范围的，超过了这个范围的x都是不可取的.

看看这个函数的极限：

由洛必达法则，

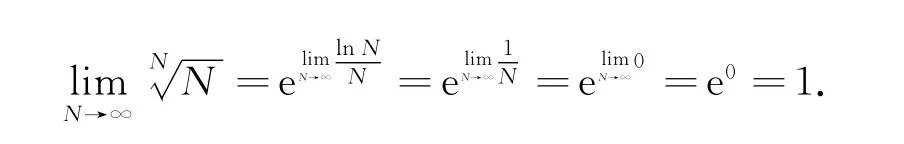
由此看来，该函数先增加到一个最大值，再逐渐递减至1.

我们对该函数求导：

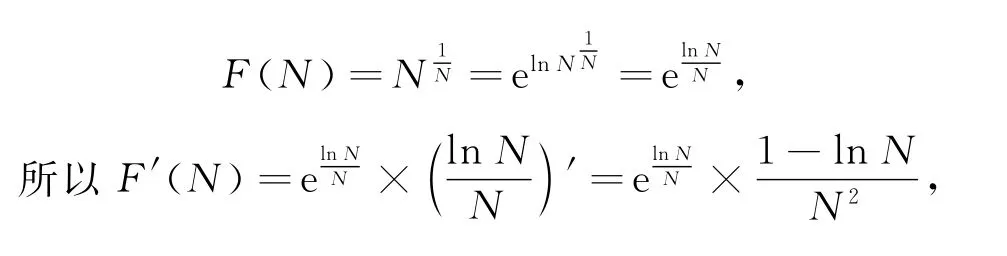
当F′（N）=0时，解得N=e，

进一步解得

其实不难理解，就如同x2=N 取N 为-1一样，我们便一眼就能看出来方程对于x∈R是无解的.那么对于∞x=4也是如此，当N=4时，方程也无意义.

可以看到由于简单直观的方法，使很多人误入了陷阱，忽略了小小的定义域从而得出了2=4的荒谬结论.祸患常积于忽微，不要为了图方便就去忽视一些看起来正确的东西，毕竟“简单直观≠正确”！