一题一世界 平淡蕴传奇—核心素养视角下的2018安徽压轴题的深度剖析

安徽省马鞍山市小马教育培训学校(243000) 范宏业

在整理安徽省2018年中考数学第23题(压轴题)的证法时,发现了一个比较神奇的情况,当我们将这些证法集中在一起时,这些证法,竟然分布于义务教育阶段所学的“图形与几何”全部内容中,几乎是覆盖了“图形与几何”的所有知识点;再透视这些证法时,除了用几何综合法外,还有“代数法”和“解析法”,也有学生用“同一法”,既有“直接法”,也有“间接法”,可以说,本题的证法,是义务教育阶段数学证明方法的大展览.透过这些证法,我们可以从中领悟到如何去进行几何证明的教学;如何去进行几何证明的复习.

1.原题及解答

(2018年安徽省中考数学试卷第23题)如图1,Rt△ABC中,∠ACB=90°,点D为边AC上一点,DE⊥AB于点E,点M为BD中点,CM的延长线交AB于点F.

(1)求证:CM=EM;

(2)若∠BAC=50°,求∠EMF的大小;

(3)如图2,若△DAE～=△CEM,点N为CM的中点,求证:AN//EM.

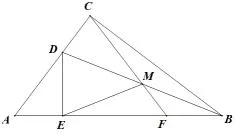
图1

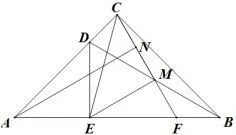
图2

1.1问题(1)典型的证法

证法一(利用“直角三角形斜边上的中线等于斜边的一半”)

因为在Rt△DCB中,∠ACB=90°,M为BD中点.所以同理所以MC=ME.

证法二(利用“四点共圆”)

因为∠ACB=90°,DE⊥AB,所以B、C、D、E四点在以BD为直径的圆周上;又点M为BD中点,所以MC=ME.(如图3)

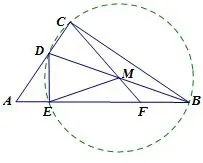
图3

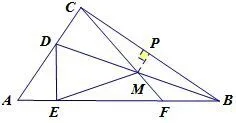
图4

证法三(利用“线段的垂直平分线的性质”)

过点M作MP⊥BC于点P,如图4.因为∠ACB=90°,所以MP//CD.又DM=BM,所以CP=BP.所以MP垂直平分BC.所以CM=BM.同理EM=BM,所以MC=ME.

(此证法是在阅卷过程中记录下的学生证明.马鞍山市的市区(花山区、雨山区)使用的数学课本为上海科学技术出版社出版的“义务教育教科书数学”,在八年级下册第81页例6后有“经过三角形一边中点与另一边平行的直线必平分第三边”.此证法虽然有点“舍近求远”,但思路清晰,过程流畅.)

1.2问题(2)典型的解法

证法一(利用等腰三角形及三角形外角的性质得出二倍角,再利用邻补角性质求之,体现整体代入的思想.)

因为∠BAC=50°,∠ACB=90°,所以∠CBA=40°.因为CM=MB,所以∠MCB=∠CBM.所以∠CMD=∠MCB+∠CBM=2∠CBM. 同理,∠DME=2∠EBM.所以∠CME=2∠CBA=80°.所以∠EMF=180°-∠CME=100°.

证法二利用“四点共圆”及圆周角推论证明.

由于B、C、D、E四点共圆(在(1)的基础上,也可以是“一中同长”得出此“四点共圆”),所以∠EMC=2∠EBC;又∠BAC=50°,所以∠CBA=40°;∠CME=2∠CBA=80°;因为∠CME+∠EMF=180°,所以∠EMF=180°-∠CME=100°.

1.3问题(3)典型的证法

根据题意,△DAE～=△CEM.所以∠CME=∠DEA=90°,DE=MC,AE=EM.

思考不能停止.若在此停止了,后面就做不下去了.此处的进一步的深入思考,是整过解题的基础.思考的越多,形成的新结论就越多,后面使用就越方便,证法就越多.真所谓是“横看成岭侧成峰”,从不同的视角,可以给出不同的解决方法.这种顺向推理,在进行几何证明训练时,一定要要求学生“多想一步”,不仅是现在的解题需要,也是创新意识培养的需要.

由(1)已证,MC=ME,所以DE=MC=AE=EM.所以△DAE,△CEM为等腰直角三角形,∠DAE=∠ADE=∠CEM=∠ECM=45°;Rt△ABC也为等腰直角三角形∠CBA=45°.又CM=DM=EM,所以DM=DE=EM.所以△DEM是等边三角形.∠MEF=∠DEF-∠DEM=30°;∠MBA=MCB=15°,∠BDC=75°

还有一些结论在后面的证明过程中展示;同时,推理得出的结论,在后面使用时,限于篇幅,就不一一证明了.下面根据证明方法根据所用的知识展现的.

1.3.1 利用平行线判定方法

这是解决本问题的最为直接,最为基本证法,思路明确.下面的证法是主要运用平行线的判定方法中的“同位角相等,两直线平行”进行展开的.对本问题来说,由于有两组“同位角”(“∠NAF与∠MEF”和“∠ANF=∠EMF”),都可以进行证明.

1.3.1.1 解直角三角形

若选择∠NAF与∠MEF作为同位角,因为∠MEF=30°,所以只要证得∠NAF=30°.

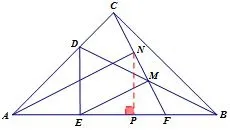
图5

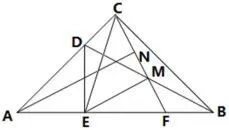
图6

证法一如图5,作NP⊥AB于P.设MF=a,则EF=2a,ME=MC=AE==在Rt△ANP中,tan∠NAP所以∠NAP= 30°. 因 为∠MEF=30°,所以AN//EM.

1.3.1.2 相似法.(先证相似得到有关的角相等,再用同位角相等证平行.)

1.3.1.2.1 构造A字型相似

证法二如图6,设MF=a,则EF=2a,ME=MC=AE=MN=所以所以因为∠EFM=∠AFN(1),所以△EFM∽△AFN(2).所以∠MEF=∠NAF(或∠FME=∠FNA)(3). 所以AN//EM(4).

也可以采用以下证法:

证法三 如图6,易证在Rt△MEF中,∠MEF=30°,有因为N是MC的中点,所以因为△DAE～=△CEM,所以所以所以后面同证法二的(1)-(4),此处略.

1.3.1.2.2 构造子母相似形

证法四如图7,设MF=a,则EF=2a,ME=MC=AE==AF=EF+AE=2a+所以又因为且∠AFN=∠NFP,所以△AFN∽△NFP,所以∠NAP=∠PNF=30°=∠MEF(∠ANF=∠NPF=90°=∠EMF),所以AN//EM.

此法也可证△APN∽△NPF.

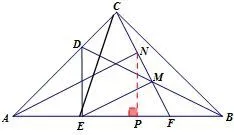
图7

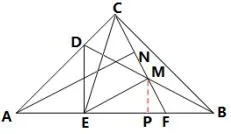
图8

证法五如图8,过点M作MP⊥AB于P,设PF=a,MF=2a,则EM=AE=CM=NM=所以因为∠MFP=∠AFN,所以△MFP∽△AFN,所以∠MPF=∠ANF=90°,所以∠ANF=∠EMF=90°,所以AN//EM.

1.3.1.2.3 面积法

利用面积法证线段成比例,得到相似,从而证明平行.

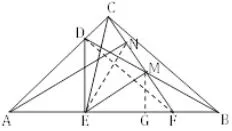
图9

证法六连接NE,DF,作MG⊥AB,垂足为G,如图9.因为N是中点,所以S△CEM=2S△MEN.易证MG=DE,所以S△DEF=2S△MEF.因为=后面的证明过程就不再赘述了.

上面的证法主要是围绕∠MEF=∠NAF展开的.

若选择∠ANC与∠EMC作为同位角,因为∠EMC=∠AED=90°,所以只要证得∠ANC=90°.根据已知条件证得“AM=AC”,而点N为CM中点,由等腰三角形“三线合一”即可得到AN⊥CM.进一步∠EMC=∠AED=90°,从而AN//EM.下面围绕证明“AM=AC”这一思路进行证明.

在证明“AM=AC”可采用“代数法”与“几何法”,代数法即利用勾股定理等方法将AM与AC用含相同参数的表达式表示出来,几何法:(1)若两条线段不在同一三角形中,常通过证明全等得出结论;(2)若两条线段在同一三角形中,可以通过“等角对等边”加以说明.

1.3.1.2.4 等腰三角形

在证明AM=AC得到△ACM位等腰三角形时,也有着多种证法,先用“代数法”.

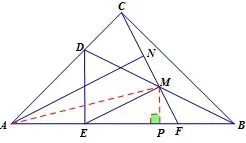
图10

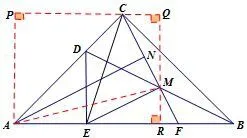
图11

证法七如图10,连结AM,作MP⊥AN于P.设AE=ME=2a,因为∠MEB=30°,所以MP=a,EP=BP=所以AM2=AP2+MP2=(2a+)2+a2=(8+4)a2,AC2=AB2=(2a+2)2=(8+4)a2,所以AM=AC.又N为CM中点,所以AN⊥CM,而EM⊥CM,所以AN//EM.

也可以采用如图11的作图,从而形成新的计算AM、AC的计算方法.

证法八构造如图11所示的矩形,设AE=ME=2a,因为∠MEB=30°,所以MR=CQ=a,ER=MQ==QR=a+所以AM2=AP2+MP2=(2a+)2+a2=(8+4)a2,AC2=2AP2=2(a+)2=(8+4)a2,所以AM=AC.后面的证明就不再赘述了.

1.3.1.2.5 等角对等边

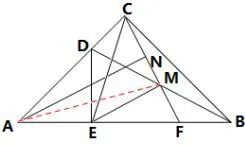
图12

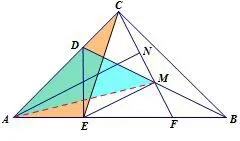
图13

连接AM后,线段AM、AC位于同一三角形中,可能会想到“等角对等边”这一方法,再利用等腰三角形中的三线合一的性质.下面的几种证法从不同的视角证明了AM=AC.证法九如图12,连接AM,则∠EAM=∠EMA=∠MEF=15°,所以∠AMC=∠EMC-∠EMA=75°,①又∠CMD=∠EMC-∠EMD=30°,且MC=MD,所以∠ACM=(180°-30°)=75°,②由①可知AC=AM,又N为CM中点,所以AN⊥CM,而EM⊥CM,所以AN//EM.

从“证法九”中,我们看到,若能将题目中的条件充分挖掘,此法的思路自然是清晰明了、水到渠成.

1.3.1.2.6 全等法

三角形全等是证明线段相等的最常规办法,可以利用原图或采取构造的方式寻找全等三角形.

证法十(全等法1)如图13.连接AM,在△ACE与△MAD中,因为AE=MD,∠AEC=∠MDA=105°,CE=AD,所以△ACE～=△MAD(SAS).所以AC=AM.再用等腰三角形“三线合一”或“全等”证得AN⊥CM,而EM⊥CM,所以AN//EM.

联想到等腰三角形三线合一的性质,证∠ANM=90°或∠ANC=90°.

证法十一 (全等法2)连接AM,如图14.先证明△DEM是等边三角形,可以得到∠CMD=∠MEF(不必写出 30°),从而得到∠CMB=∠MEA,在△AEM与△CMB中,易证AE=CM=EM=MB,且∠AEM=∠CMB=150°,所以△AEM～=△CMB(SAS),所以AM=CB.所以AC=AM.后面的证明就不再赘述了.

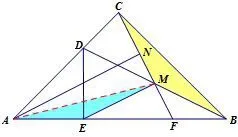
图14

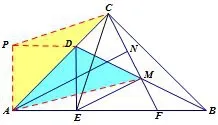
图15

以下还有几种巧妙构图方式,也可以通过全等证明AC=AM,限于篇幅,只给图形,不在进行文字说明.

证法十二(全等法3)构造如图15所示图形,证明△APC～=△ADM.

证法十三(全等法4)构造如图16所示图形,证明△APC～=△AEM.

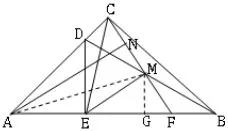
图17

证法十四(全等法5)如图17,连接AM,过点M作MG⊥AB,垂足为点G.易证在Rt△MEF中,∠MEF=30°,所以MG=EM.因为N是MC的中点所以MN=MC.即MN=EM.所以MG=MN.易证∠CMG=150°,且易求∠AMG=75°. 所以∠AMN=75°,所以△AMN～=△AMG(SAS).所以∠ANM=∠MGA=90°.后面的证明就不再赘述了.

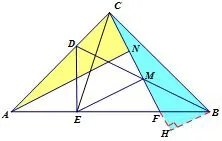
图18

证法十五(全等法6)如图18,过点B作BH⊥CF于点H,又EM⊥CM,所以EM//BH,得△BHF∽△EMF,∠FMB=∠FBM=30°,所以MF=BF.在 Rt△EMF中,∠FEM=30°所以MF所以又MN=CN=EM,所以CN=BH.因为∠NCA=∠HBC=75°,AC=CB,所以△NCA～=△HBC.因为∠ANC=∠CHB=90°,所以AN⊥CM.又EM⊥CM,所以AN//EM.

此种证法,就是我们在讲解三角形全等时的一个重要模型:一线三等角全等法,在此是异侧型“一线三直角全等”.

1.3.2 直角三角形斜边中线等于斜边一半

证法十六如图19,分别延长CA、ME交于点P,在AP上截取AQ=CD,△AEQ～=△DEC,则通过角的关系变化,可得∠P=∠QEP=15°.所以PQ=QE=CE=AD,所以AP=AC,即点A为PC中点,由直角三角形斜边中线等于斜边的一半,可知AM=PC=AC.

还可以进行这种巧妙构图:

1.3.3 运用“中位线定理”

证法十七如图20,延长CA,ME交于点G,过A作AP⊥AB于A,交EG于P.易证△APE～=△MFE,得AP=MF=FB,∠APE=∠MFE,所以∠APG=∠CFB. 又∠GAP=∠CBF=45°,所以△GAP～=△CBF,AG=BC=AC.又CN=MN,所以AN//EM.

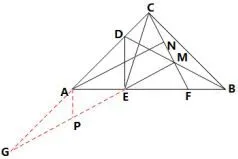
图20

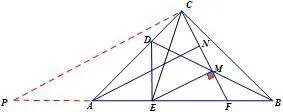
图21

1.3.4 运用“平行于同一条直线的两条直线平行”

因为平行于同一条直线的两条直线平行,因此,此题可以构造AN、EM之外的“第三方直线”,通过平行的传递性予以解决.

证法十八如图21,过点C作CP//ME交BA延长线于点P,则∠CPE=∠MEF=30°.在△ECP与△DAB中,因为∠CPE=∠MEF=∠ABD=30°,∠CEP=∠ADB=105°,CE=AD,所以△ECP～=△DAB(AAS),所以PE=BD=2AE,即点A为PE中点,所以AN为梯形MCPE的中位线,所以AN//CP//ME.

此法也可采用倍长EA再证全等或构造母子型相似解决.

1.3.5 构造含对边平行的特殊图形

在初中阶段,我们学习了多种含对边平行特征的图形,如:平行四边形、矩形、菱形、正方形、梯形等,特别是平行四边形类图形只要证得其中一组对边平行,另外一组对边也就平行,此题用这种思路解决甚为巧妙.

1.3.5.1 构造平行四边形

证法十九如图22,过点N作AB的平行线交EM的延长线于点P,所以∠P=∠MEB=30°,所以PN=2MN=CM=AE,因为PN//AE,PN=AE,所以四边形AEPN是平行四边形,所以AN//EM.

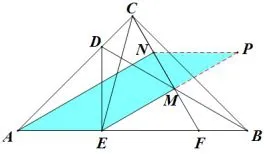
图22

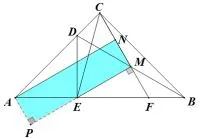
图23

1.3.5.2 构造构造矩形

证法二十如图23.根据此图形易证AN//EM,限于篇幅不再赘述.

1.3.5.3 构造菱形

证法二十一(倍长中线法证明线段平行)如图24,倍长中线.延长AN至G,使NG=AN,则四边形ACGM是平行四边形.再证AC=AM,则ACGM是菱形,而菱形的对角线相互垂直,因此,AN⊥CM.后面的证明就不再赘述了.

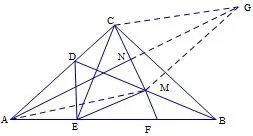
图24

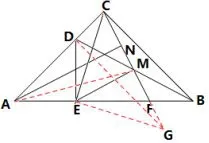
图25

1.3.6 轴对称法

证法二十二如图25,易证△AED和△EMC是等腰直角三角形,所以DE=DM=EM,△DEM是等边三角形,∠CMD=∠MEF=30°.将△CEM沿EM折叠至△GEM,易证△AEC～=△DEG.所以∠EDG=∠CAE=45°,∠MDG=∠MGD=15°. 因为∠DMG=∠AEM=150°,所以△AEM～=△DMG.所以AM=DG=AC,△ACM为等腰三角形.因为CN=MN,所以AN⊥CM.又EM⊥CM,所以AN//ME.

1.3.7 旋转法

证法二十三如图25,将△CEA绕点E按顺时针旋转90°得△DEG.

1.3.8 解析法

证法二十四以点C作坐标原点建立平面直角坐标系,如图26.证线段平行,即可证明线段所在的直线的斜率相等.设点A(a,0),D(b,0),易证△ABC为等腰直角三角形,则B(0,a),所以lAB:y=-x+a,易得△ADE是等腰直角三角形,则有lDE:y=x-b.由解得:因为M是BD的中点,N是MC的中点,所以因为DM=DE,又DM=在 Rt△ADE中,DE=所以即a2-4ab+b2=0;若AN//ME,则必有kAN=kME,则有化简得:a2-4ab+b2=0,即证.(此证法是在阅卷过程中记录下的学生证明.)

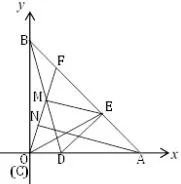
图26

图27

1.3.9 同一法

证法二十五如图27,过点A作AN′⊥CF于N′,易证△DEM 为等边三角形,从而∠MEF=30°,∠MFA=60°,∠N′AF=30°,N′F=AF.令MF=a,则EM=AE=CM=EF=2a, MN′=MN′=CN′,得N′为CM 的中点.又N 为CM 的中点,N′与N 重合,得证AN//EM.(此证法是在阅卷过程中记录下的学生证明.)

1.3.10 运用“余弦定理”

证法二十六设MF=a,利用余弦定理(超纲)求得(或解形求之),再求AF2-NF2=所以AN2=AF2-NF2,利用勾股定理的逆定理得到∠ANF=90°,从而得∠ANF=∠EMF,得到AN//EM.(此证法是在阅卷过程中记录下的学生证明.)

1.3.11 三角形函数中的倍角公式

本法的特点是利用二倍角公式和相似.

证法二十七设CM=BM=a,∠MCB=∠MBC=15°,所以BC=BDcos15°=2CMcos15°=2acos15°=AC,因为∠CMD=30°,∠CDM=∠DCM=75°,所以CD=2CMsin15°=2asin15°,所以CD·AC=4sin15°cos15°a2=a2=CM2=12CM·2CM=CN·BD.即又∠CAN=∠BDC=75°,所以△BCD∽△ANC,所以∠ANC=∠BCD=∠EMF=90°.所以AN//EM.(此证法是在阅卷过程中记录下的学生证明.)

2.对中考复习的启示

在中考的总复习过程,教师要十分重视学生对基础知识的梳理和复习,即使是这样的压轴题,除了后面几种解法超出《课程标准》外,其他方法都是基本方法.当然,此题方法肯定还有很多,有待继续探索和补充.对几何学习而言,真是所谓“做百题不如吃透一题”.

无论是在总复习时,还是在平时的几何教学中,教会学生面对几何问题时的分析方法,如何从已知条件进行正向推理,也就是所谓“由因导果”;如何根据所要证明的问题进行逆向溯源,寻找成立的条件,即所谓的“执果索因”倒推;还有,从条件出发向前推理,从结论出发寻找成立的条件的“两头凑”的方法,做到进退有序,寻找条件与结论的联结点从而轻松解决问题,将这些分析的方法变成面对几何问题时的思维习惯.

在几何教学或复习中,一定要向学生说明,数学的阅读,其实是一个“推理式深加工阅读”,在阅读的过程中,要边阅读边思考,要善于联想,并进行发散式思维,要尽可能多想一点,不仅是看清其字面意思,更重要的要能读“弦外音”,想到“话中有话”,可以说是典型的“由表及里,由此及彼,推陈出新”的过程.这一切,都需要学生在平时学习养成好的“推理式深加工阅读”的习惯,对条件进行发散式思考,这种思考方式,不仅可以促进现在的数学解题,也可以培育学生的创新思维,为学生的未来发展奠定基础,即所谓的“数学使人聪明”.

3.感谢

感谢安徽省马鞍山市教育科学研究院数学教研员、特级教师刘义杰老师的指导;感谢马鞍山市成功学校汤深晶老师和他的学生(他们当时都是八年级的学生),在2018年中考结束后,我们在一起讨论本题的解法;感谢马鞍山市当涂县姑苏中学袁正千老师,他和本题阅卷组的老师,在繁忙的阅卷过程中,还不忘学生典型解法,并进行了整理;本文在整理的过程中参考了微信公众号为“三一草堂数学”李翼老师的《信息解构整合,破解压轴难题》一文中的部分解法,在此表示感谢!