成竹在胸,枝节自清—强化高中统计教学的流程意识

广东省佛山市第一中学(528000) 程生根

统计学是通过收集数据和分析数据来认识未知现象的一门科学[1].数据分析能力是统计学的核心内容也是普通高中数学课程标准中的数学学科的六大核心素养之一.学生通过学习统计学知识要达成的关键能力是经历较为系统的数据处理全过程,在此过程中学习数据分析的方法,理解数据分析的思路.解决统计问题首先要具备统计流程意识(成竹),其次才是掌握统计技术(枝节).所以在教学中既要教会学生必要的统计技术,更重要的是要学生掌握解决统计问题的一般思路,植入统计思想.统计过程的流程化是达成目标的有效的做法.

一、统计活动的整体流程意识

统计学来源于生活,作为一门应用性的数学分支,总体上是一个解决实际问题的流程(闭环结构),统计活动大体上都要遵循下面的处理流程:

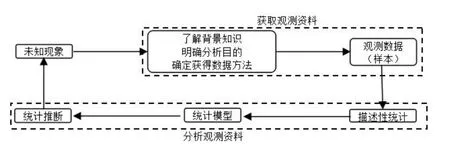
二、统计环节中的局部流程意识

(一)统计环节(收集数据、整理数据、分析数据、统计推断)流程图

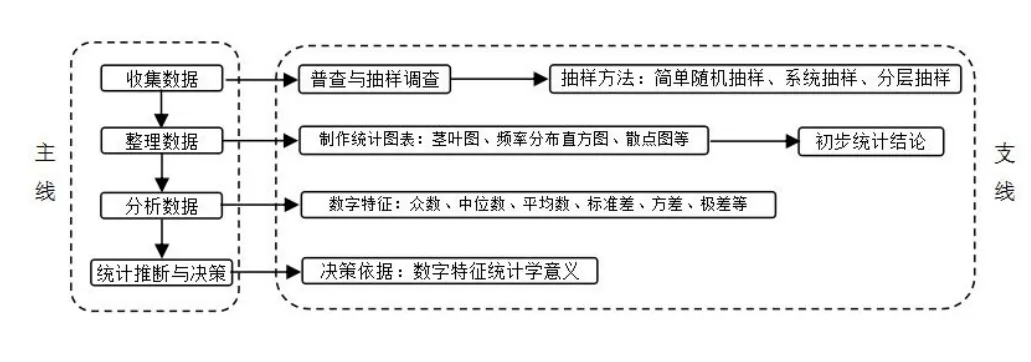
依据数字特征作统计决策,要从根本上把握各统计数字特征的统计学意义,应思考下面几个问题:1、常用的数字特征有哪些?2、各数字特征产生的背景(即产生在统计活动中的哪个环节?);3、利用哪一个(或几个)数字特征作决策?4、如何根据数值大小合理决策?应引导学生在统计活动的主线中去思考这些问题.让学生理解用均值、中位数、众数代言平均水平,用极差、方差、标准差等代言稳定程度的合理性.体会同为平均水平(或稳定程度)的不同数字特征之间的差异,及产生差异的原因.从而更深刻地体会各数字特征在统计过程中的地位及统计学意义,为科学决策服务.

(二)统计技术中的流程

统计活动不仅是要有主线意识,支线中的技术环节也各有一定的操作流程.

1、混合抽样方法的操作流程:

2、茎叶图的制作规则与流程:

3、频率分布直方图的制作流程:

三、统计模型中的流程意识

(一)回归分析与独立性检验的流程分析

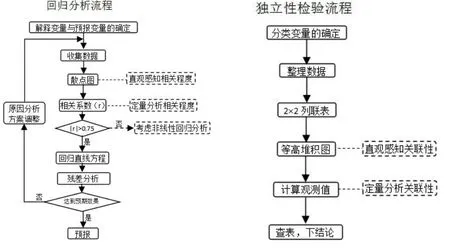
(二)借助流程理解独立性检验的决策过程

在学生做独立性检验分析时,建立了分类变量X与Y的2×2列联表,计算出K2观测值后,有些同学并不能理解为什么要查表及表中数据的含义,只是例行公事,生搬硬套,所以容易遗忘与出错.要准确理解K2观测值的大小与犯错率大小的因果关系,才能记得牢、用得准.可将教材中的分析过程简化为如下的决策思路:

结论:K越大,P(K2＞k)越小,“X与Y有关系”犯错率越小.更有把握认为“X与Y有关系”.先把思路理清,再通过查表量化犯错率.

四、高考统计试题中的流程意识

由于高考试卷的篇幅有限,命题者总会想办法在有限的篇幅里“容入”尽量多的考点、覆盖统计活动过程中尽量多的环节.因此统计试题突出的特点是阅读量大,信息量大.难点在于审题,只要考生顺利过了审题关,后面的相关计算反而简单了.审题时要抓住统计活动的“主线”,分析合理性,排除干扰因素,计算相关的样本数字特征,用样本数字特征估计总体数字特征,做出合理决策.

下面以2018年全国卷的三个统计题为例,分析试题的主线与考点设置:

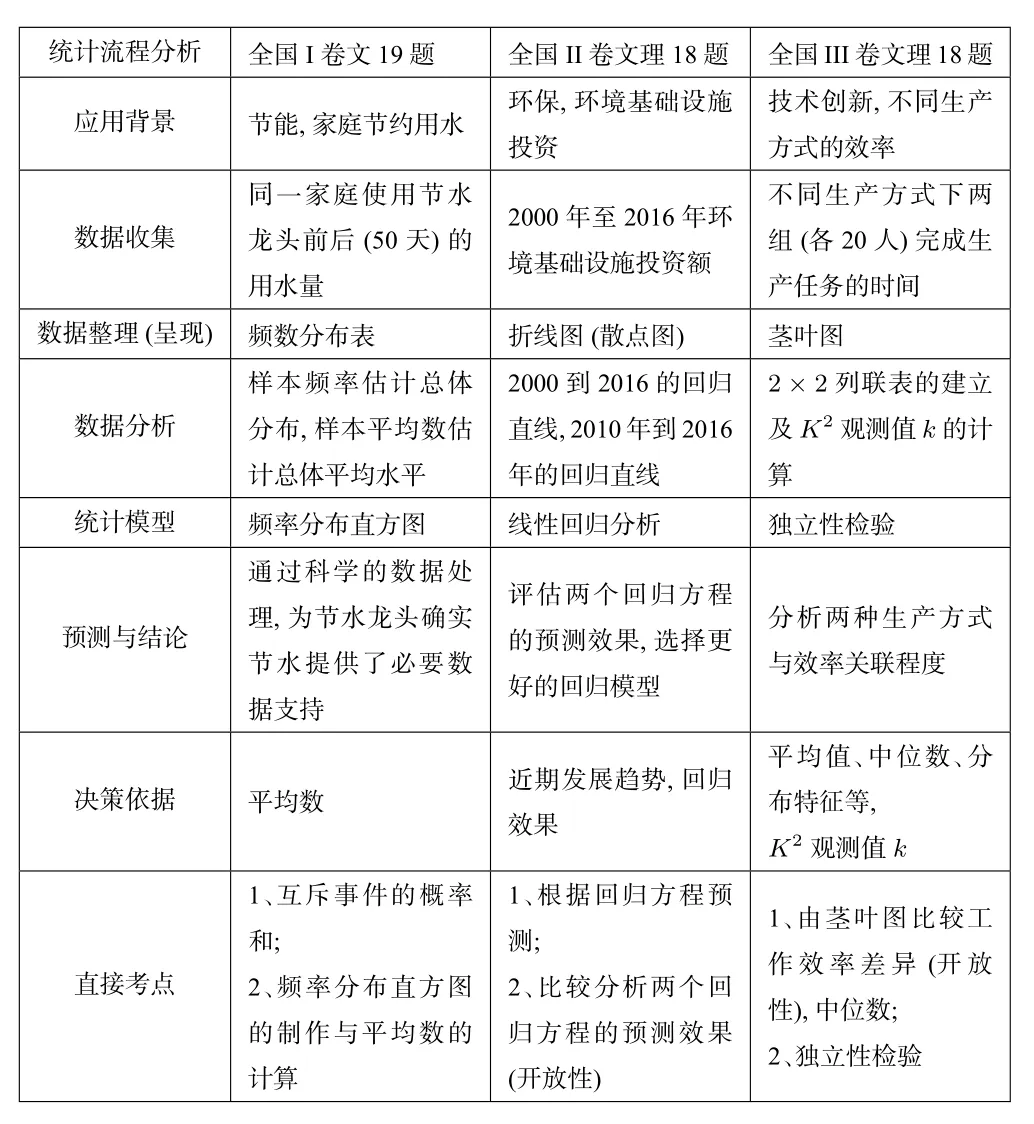
统计流程分析 全国I卷文19题 全国II卷文理18题 全国III卷文理18题应用背景 节能,家庭节约用水 环保,环境基础设施投资技术创新,不同生产方式的效率数据收集同一家庭使用节水龙头前后(50天)的用水量2000年至2016年环境基础设施投资额不同生产方式下两组(各20人)完成生产任务的时间数据整理(呈现)频数分布表 折线图(散点图)茎叶图数据分析样本频率估计总体分布,样本平均数估计总体平均水平2000到2016的回归直线,2010年到2016年的回归直线2×2列联表的建立及K2观测值k的计算统计模型 频率分布直方图 线性回归分析 独立性检验预测与结论通过科学的数据处理,为节水龙头确实节水提供了必要数据支持评估两个回归方程的预测效果,选择更好的回归模型分析两种生产方式与效率关联程度决策依据 平均数 近期发展趋势,回归效果平均值、中位数、分布特征等,K2观测值k直接考点1、互斥事件的概率和;2、频率分布直方图的制作与平均数的计算1、根据回归方程预测;2、比较分析两个回归方程的预测效果(开放性)1、由茎叶图比较工作效率差异 (开放性),中位数;2、独立性检验

试题特点与教学启示:

(一)背景贴近生活,社会热点的节能、环保、技术创新等方面;

(二)试题材料体现统计过程,数据直接呈现,减少繁杂运算,考查重心是数据的分析和理解,突出考查对数学思想的理解与运用能力;

(三)增加了试题和答案的开放性,鼓励考生从多角度作答,引导数学教学从培养学生“解题”到“解决问题”,引导学生从“做题”到“做人做事”素养的提升.

五、教学素材开发示例

要让学生养成用流程的眼光去思考统计问题的习惯,形成自觉的数据处理意识,就一定要在教学中精选或精编例题与习题,提供相应的教学素材,学生通过对素材的学习与理解达成预设的目标.下面是本人原创的三个例题及例题分析,权当抛砖引玉.

例题1某地区“腾笼换鸟”的政策促进了区域内环境改善和产业转型.现从当地天气网站上收集该地区近两年11月份(30天)的空气质量指数(AQI)(单位:μg/m3)资料如下:

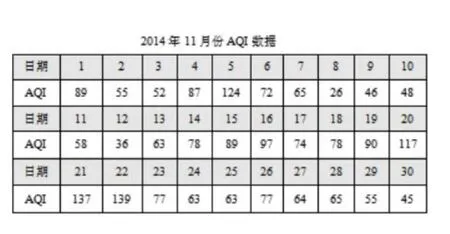
(I)请完成2014年11月份AQI数据的频率分布直方图;

(II)根据以上的数据或图表,该地区空气质量比去年同期是否有所改观,说明理由?

分析本题以现实社会生产实践中的中的环境保护问题为背景,数据来源为气象部门的真实数据,贴近生活,第一问给出上一年同期的频率分布直方图,这样的设计是为了避免陷入繁琐重复的工作,也为制作频率分布直方图提供参照,便于直观上的对比分析.覆盖的知识点有数据整理、频率分布直方图的识别与理解,体验频率分布直方图的制作过程等.第二问为开放问题,根据前后数据对比,用数据说话,可以通过定量计算比较优良率、均值、方差等作决策,也可以对比两个频率分布直方图的形状直观分析作决策.本题引导学生经历了从数据收集整理、频率分布直方图的识别理解与制作、数据处理与分析应用能力的全过程,有助于学生建立统计知识的流程意识.

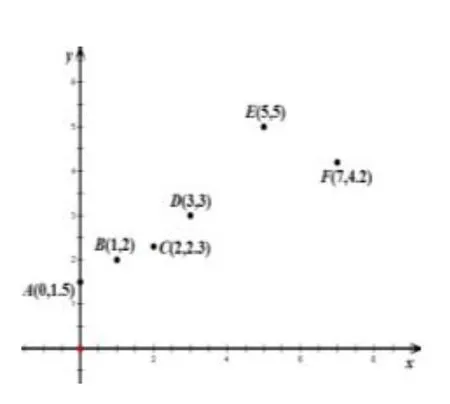
例2某同学用收集到的6组数据对(xi,yi)(i=1,2,3,4,5,6)制作成如图所示的散点图(点旁的数据为该点坐标),设由这6组数对计算出的相关系数为γ,回归直线l的方程为:ˆy=ˆbx+ˆa.分析下面三个结论:1○γ＞0;②直线恰好经过点D;③ˆb＞1.其中正确的结论个数是( )

A.0 B.1 C.2 D.3

分析本题覆盖了散点图、相关系数、样本点中心、最小二乘法等线性回归分析的诸多重要知识点.解答时应引导学生从定性描述与定量分析两方面的结合.比如②需要通过定量运算才能确定,①③都可通过定性的分析便可分辨正误,其中处理③时,注意到DE两点连线斜率已是1,此时直线DE“不够”贴近样本点,回归直线应该更“缓”.本题引导学生体会线性回归分析的全过程,从感性理解到理性分析,既有助于基本知识的掌握,也能发展学生的关键能力.

例3有甲乙两家公司都愿意聘用某求职者,这两家公司的具体聘用信息如下:

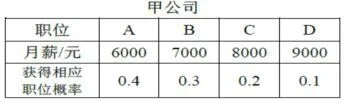
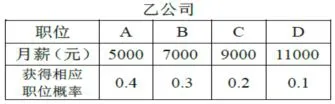
(I)根据以上信息,如果你是该求职者,你会选择哪一家公司?说明理由;

(II)某课外实习作业小组调查1000名职场人士,就选择这两家公司的意愿作了统计,得到如数据分布:

小组对选择意愿与年龄这两个变量作独立性检验分析,计算得到K2的观测值为k=5.5513.请用统计学知识分析:选择意愿与年龄变量和性别变量中哪一个关联性更大?

分析本题以求职意愿差异,及产生差异的原因为背景,试题设计自然流畅,情节相对完整,体现统计活动的过程性.第一问通过计算对比两家公司的薪酬平均水平与稳定水平做出求职选择,本问是开放的问题,不同的人可能做出不同的选择,只要能够说出理由即可,鼓励考生从多角度作答,引导数学教学从培养学生“解题”到“解决问题”.第二问是分类变量独立性检验问题,分析导致选择差异的可能因素,并通过比较选择意愿与年龄变量和性别变量的关联性大小,要计算K2观测值,作为独立性检验流程中的一环,建立2×2列联表是隐含的任务,为了避免学生陷入繁琐重复的数值运算,题目给出其中一个的K2观测值,把考查重点转移到对模型的比较与判断,体现了统计方式的应用价值,培养学生能够根据任务要求选择合适的数据的能力[4].

高中生从小学便开始接触统计学知识,总体是一个螺旋上升的过程.小学初中的统计知识以感性认知与计算为主,高中阶段的统计知识以理性分析为主,逐步培养主动的数据处理意识.所以高中统计教学中不能过于关注统计技术手段,计算技巧等.要防止把统计教成算术.更重要的是要根植统计思想.分析处理统计问题之前,统计活动整体流程要了然于胸.当下工作处于统计活动哪个环节?每个数据有什么统计学意义?先明白为什么要算?再考虑怎样算?引导学生形成自觉的数据分析意识,提高高中学生的统计学素养水平.