一节初中“实践与探究”课的教学设计与反思—基于数学素养的视角

海南省中央民族大学附属中学海南陵水分校(572400) 韩芳蓉

当前,随着新课程改革在全国各省市如火如荼地进行着,培养和提高学生的数学素养已经被越来越多的一线教师所重视,并努力着将其落实到每一节的教学过程中.本文结合华东师大版七年级数学第六章“实践与探索的问题1”这一内容,浅谈如何在教学设计中渗透数学思想和方法,培养学生良好的数学思维习惯,提高学生数学问题的解决能力,以期培养学生的数学素养.

1.设计思路

地位与作用:利用一元一次方程解决实际问题,是中学阶段应用数学知识解决问题的开端,也是让学生体会数学的价值性,增强学生学数学、用数学意识的重要题材,教材中所渗透的数学建模思想、归纳、类比、化归等思想方法,都是学生今后学习和工作中必备的数学素养.

学情分析:学生已经熟练掌握一元一次方程的求解,并且在前一节实际问题内容的学习中,熟悉了列方程的基本思想和步骤.但是应用一元一次方程解决实际问题的学习对于初一的学生是一个重点,更是一个难点,学生在学习这部分内容时往往容易在心理上产生惧怕的情绪,尤其是一些基础比较差的学生.因此,这一内容的教学不能一步到位,要循序渐进,遵循由简到难,特殊到一般的认识规律,让学生更好的理解和掌握.

教法分析:采用引导启发式、实践探究式、小组合作式相结合的教学方法.以“问题”引导启发学生思考,以“实践探究”,结合变式训练,由浅入深,引导学生灵活掌握,以“自觉分析”的方式引导学生总结归纳,诱导学生“自发领悟”,从而学会理解数学.

教学重点:让学生在实践和探索的过程中体会数学建模思想,培养学生应用数学知识解决实际问题的能力.

教学难点:在实践活动中借助直观的图形来列方程,学会灵活设未知数:直接设未知数和间接设未知数.

教学用具:多媒体、铁丝等教学手段,起到辅助学生的探究实践环节,提高课堂效率的作用.

2.教学设计

2.1.温故知新

(1)列一元一次方程解应用题的步骤是什么?

(2)常见几何图形的周长、面积以及常见立体图形的体积公式,填表.

师生活动:学生思考后回答,常见图形的周长、面积、体积公式以表格形式作为预习作业,并在课前进行小组交流,学生以小组为单位进行汇报.

(设计意图:针对班级一部分学生的小学基础较差的情况,温故知新,将图形的周长、面积、体积公式作为预习作业,并且在小组交流中加深印象,为本节新知的学习做好铺垫.)

2.2.探究

问题:用一根长60厘米的铁丝围成一个长方形.

(1)动手实验,可以围成多少个长方形?

(2)如果长方形的长是20厘米,那么宽是多少?这个长方形的面积是多少?若设宽为x,则方程怎样列?

(3)长方形的长、宽和周长由什么关系?若用铁丝围长方形,根据以上关系,怎样围长方形比较快捷?

师生活动:学生动手实践,思考交流,体会周长一定的长方形有无数多个,当添加一个条件“长是20厘米”,学生能快速反应到这样的长方形是唯一并且是具体的.

(设计意图:让学生动手操作,感受当周长一定时,长方形的形状有“瘦”“胖”无数多种.当确定“长是20厘米”时,学生能快速地利用算术法和方程法求解问题,并能深刻感受到“长与宽的和等于周长的一半”这个事实,从简单的问题入手,从学生思维的最近发展区出发,经历动手实践、观察、验证的过程,让每个学生尤其是基础较差的学生都能参与到数学活动中.)

2.3.实践

师生活动:学生思考,分组完成不同的设元方法,最后进行比较和归纳.

(设计意图:引导学生比较不同的设元方法,体会解决问题的方法是多样的,并且由于设元的不同,未知量的表示以及方程都会发生变化,进而归纳出合适设元的方法.)

(2)使长方形的宽比长少4厘米,求这个长方形的面积?若设长方形的面积为x平方厘米,能否直接列方程?

(设计意图:学生通过对这一串问题的探究,思维上升了一个层次,能充分意识到:随着条件的变化,产生了不同的问题,进而有不同的答案.经历了简单模仿——变式训练这两个过程,学生能意识到不能直接设元,而是关注长方形的“长”和“宽”,将长方形的周长与面积连接起来,体会间接设元的方便.)

(3)动手实践,用铁丝围成长方形,互相比较哪个长方形的面积最大?并完成以下表格(见表1).(小组合作)

表1

师生活动:学生通过小组合作探究,计算并完成表格.

(设计意图:周长一定时,不同的条件得到具体的长方形的面积是不一样的,学生带着一定的疑惑和强烈的探究欲望,进行小组合作探究.让所有学生主动地思考、探究、做数学,并在其中提出自己的猜想,进而随着探究得到一步步地验证.)

2.4.归纳

(1)观察表格,你发现长方形的面积有什么变化?

师生活动:学生借助表格进行分析和比较,派代表发言,鼓励学生用自己的语言表述结论,教师引导纠正.

(2)阅读:教材第17页“读一读”.

(设计意图:以学生为主体,培养学生口头表达能力,引导学生积极参与探究活动和归纳表达,在知识的“再创造”中理解数学,感受数学,以探究活动为载体培养学生的数学素养.)

2.5.拓展,欣赏数学之美

(1)通过以上结论,猜想以下结论:a、b均为正整数:

①若a+b=10,则ab的最大值是多少?

②若a+b=16,则ab的最大值是多少?

③若a+b=20,则ab的最大值是多少?

④若a+b=22,则ab的最大值是多少?

⑤若a+b=n,则ab的最大值是多少?

(设计意图:从几何问题拓展到代数问题,引导学生感受数形结合的重要数学思想,利用从几何中获得的结论解决代数问题,获得成就,通过对知识的深入挖掘,发展学生的数学思维能力.)

(2)为什么蒙古包设计成圆形的,为什么植物中的“根”“茎”的横截面是圆形的?

师生活动:教师展示蒙古包以及植物的“根”“茎”横截面照片,学生思考后回答.

(设计意图:寻找数学与实际生活的联系,回归生活,培养学生利用数学思考问题和解决问题的能力,让学生感受到自己熟悉的生活情境和大自然中隐藏着丰富的数学知识,学会欣赏数学,有效地减少学生对数学的枯燥感和畏惧感.)

(3)总结归纳,自觉分析.教师结合罗增儒教授在《数学解题学引论》[1]中总结的通过解题学解题的经验,将自觉分析投入到教学实践中.利用解题结构图(图1),帮助学生梳理和总结整堂课的解题探究过程,引导学生剖析题目的更深层次的结构,培养学生的思考问题、分析问题以及解题反思能力,充分发挥了教师的引导示范作用.

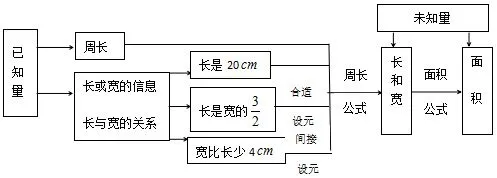
图1

(设计意图:通过对整个解题过程的分析,学生清晰地看出已知量与未知量之间是如何进行联系的,特别是当已知量是周长以及长与宽的关系,而求面积时,很显然已知量与未知量之间需要“长和宽具体值”来连接,引导学生顺利地突破“间接设元法”这个难点,当学生学会分析已知量与未知量之间的关系,找到它们连接的桥梁,即学会了解题,亦掌握了学解题的方法.)

2.6.巩固

(1)将一个底面直径是10厘米,高为36厘米的“瘦长”形圆柱锻压成底面直径为20厘米的“矮胖”形圆柱,高变成了多少?

变式:一块长、宽、高分别为4厘米、3厘米、2厘米的长方体橡皮泥,要用它来捏一个底面半径为1.5厘米的圆柱,它的高是多少?(精确到0.1厘米,π取3.14)

师生活动:学生独立完成,然后派代表发言.

(设计意图:让学生对这组课堂习题的思考,接触和理解其他几何问题类型的应用题,让前面获得的解题经验进行分析、运用,解决问题,获得自信.)

2.7.总结

通过本堂课的学习,你有什么收获?还有哪些疑惑?你能总结利用方程解决几何问题的哪些解题经验吗?

(设计意图:课堂小结,不仅梳理知识,还要总结数学思想方法,使得数学素养得到升华.)

3.教学反思

《义务教育数学课程标准(2011年版)》明确指出“综合与实践”的设置目的——“培养学生综合运用有关的知识与方法解决实际问题…培养学生的应用意识,积累学生的活动经验…”.[2]由此可见,“实践与探索”课的教学目标并不仅仅在于知识与方法的运用,而更多地希望学生“结合实际情境,体验解决问题的过程,会反思参与活动的全过程,进一步获得数学活动经验”[2],实现数学素养的提升.教师的教学过程应注意以下几点:

3.1.问题导向,启发思考

数学核心素养是一种综合性的数学能力,培养学生的数学素养,要善于以“问题”启发学生思考,以“问题”引导学生实践探究,培养学生的应用意识.较好的“问题”设计,能促进教师和学生的有效沟通,是提高学生自学能力和思维能力的一种有效方法.本课将教材内容进行整合,以“问题串”的形式展开,顺利地引导学生理解“合适设元”的优势,“间接设元”的必要性等,起到了较好的效果.

3.2.活用教材,创设数学探究情境

教师应该充分利用教材,选取贴近生活的情境,如本节课利用蒙古包和植物的相关例子,让学生发现数学之美,领悟数学思想方法,将数学文化渗透于数学课堂.培养学生的数学素养,要改变传统的教师“满堂灌”的教学模式,让学生成为课堂的主体,让他们拥有自我探索,用数学思想方法解决问题的机会,更要让学生有表现自己和展示自己的机会.重视学生实际操作、合作探究、“做数学”,获得基本数学活动经验的过程,是培养学生的数学素养的关键点.

3.3.自觉分析,培养解决问题能力

培养学生的数学素养,要及时帮助学生总结归纳,分析解题过程,暴露解题思维的“第二过程”,提取其中的数学思想和方法,挖掘题目本身的本质特征,提高学生的思维能力.本课并不是习题课,但是以探究课的形式,以“问题”为载体,完整地向学生展示了解题探究,解题分析,解题反思的全部过程,让学生能从其中学会分析问题,学会寻找已知和未知的联系,掌握学数学的方法,能真正的“理解”数学,喜欢数学.数学思想方法的培养能够促进数学核心素养的提升.[3]自觉分析,使得数学素养得到升华.

总之,中学生数学素养的培养和提高不是一两节课就能实现的,但是必须靠每一节课的精心设计去落实,将数学素养的培养转化为有效的教学行为.