平面与圆柱斜截线的深度学习

上海市宝山区教育学院(201999) 王凤春

上海市行知中学(201999) 李晓郁

在核心素养的概念中,强调的自主发展、合作参与、创新实践,这些靠传统的教学模式无从发展.大量研究表明,高阶思维能力的发展需要高阶学习活动予以支持.当学生达到高阶思维活动时,他便进入了深度学习状态,因而,在日常的课堂教学实践中,将深度学习作为一种重要的学习方式,是一条发展学生核心素养的有效途径.深度学习的价值体现不仅在于学生获得了什么学习成果,更在于学生学习过程和方式的实质性改变.

一、发现学习主题,捕捉学生思维的火花

学习主题是学生研究的对象和实践的客体.在立体几何教学时,有学生提出:平面与圆柱的斜截线一定是椭圆吗?我给出了肯定的回答,同时,我也很快意识到这是一个很好的深度学习主题,于是,我要求学生课外完成证明.

第二天,多数学生给出了如下证明.

如图1,在斜截面内以AC所在直线为x轴,AC中点O为原点建立直角坐标系,在底面内以AB所在直线为x′轴,AB中点O′为原点建立直角坐标系.

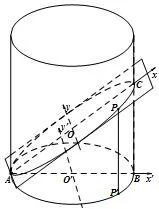
图1

设截线上任意一点P(x,y),底面圆的方程为x′2+y′2=r2,斜截面与底面所成的二面角为θ,过点P作底面的垂线交底面于点P′,则P′(xcosθ,y),所以(xcosθ)2+y2=r2,即因而,平面与圆柱的斜截线一定是椭圆.椭圆的短半轴等于圆柱底面的半径r,长半轴等于rsecθ,因而,离心率为sinθ.

二、深化学习主题,激发学生探求的欲望

对完成的同学给予表扬,并提出了如下问题.

定义1记圆柱C的底面半径为r,高度可以向上下两个方向无限延伸,这样的圆柱叫母圆柱;圆柱的斜截面与圆柱的交线叫斜截线.在圆柱内,半径为r,且与斜截平面相切于一点的球叫圆柱的焦球.

定义2平面内一定点F和一定直线AB,从平面内的动点P向AB引垂线,垂足为M,若|PF|:|PM|=e为一定值,且0＜e＜1,则P点的轨迹是椭圆.直线AB称为准线,定点F称为焦点.[1]

命题1圆柱的斜截线是椭圆.焦球与斜截面的切点F为椭圆的焦点.焦球与圆柱切线所在的平面与斜截面的交线是椭圆的准线.[2]

命题2任意椭圆都有一个母圆柱.

请同学们课后思考,能否根据上述定义用几何法给予证明?

问题的给出,激发了学生极大的探索欲望,学生们跃跃欲试,由于学习主题对空间推理能力要求很高,因而,全班仅有2位同学独立完成,6位学生群策群力,合作给出了如下证明.

证明命题1:如图2,D是截面曲线上任一点,AC是斜截面和轴面的交线,A、C是斜截面和轴面上母线的交点,作焦球切截面于点F、切轴面上母线于点L、I,过D的母线交焦球于点G,过D作平面LGI和斜截面交线的垂线,垂足为点E,过D作平行于底面的平面交母线BI于点H、交AC于点J,直线LI与直线AC交于点K.因为DF=DG=HI,DE=JK,所以DF:DE=HI:JK=CI:CK=e＜1.即截线上任意一点满足定义2,所以截线是椭圆,同理作出另一个焦点和准线.

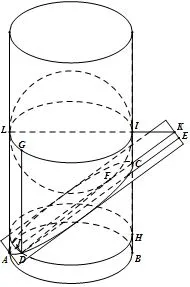
图2

命题2:利用上图,已知椭圆ADC,A、C是长轴顶点,KE是准线,F是焦点.因为,DF和DE的长度可测,即DF:DE的值可知,利用DF:DE=CI:CK=CB:CA可求得BC和BA的长度,从而确定点B的位置,以AB为底面直径、BC为母线可做出椭圆ADC的母圆柱.

三、俯视学习主题,引导学生了解数学内部的统一性

在学生兴致正浓时,我又给出了如下问题.

命题3平面与圆柱面斜截线的展开图是余弦型曲线.

这再次点燃了学生的激情,大部分学生完成了如下证明.

设圆柱高AB=2h,底面半径为r,椭圆上任取一点P,则直线O1B在平面O-xy的方程为即设∠AOP1= θ,则点P在O-xyz下的横坐标为xP=rcosθ,代入(*)得yP=hcosθ+h.如图3,将圆柱侧面沿母线AB剪开展在平面x1Ay1上,并设P在此平面上的坐标为P(x,y),则显然有x=弧AP1=rθ,所以代入上式得由此证明了命题3的正确.

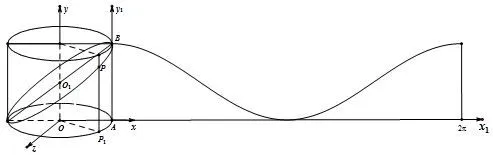
图3

四、厘清深度学习,着力发展学生的核心素养

基于核心素养的深度学习是指学习者在心流的状态下,运用高阶思维,将所学的知识和技能应用到新的复杂情境的认知过程,并逐步形成正确的价值观和必备品格.深度学习的提出,既是对教学规律的尊重,也是对如何落实立德树人的主动回应.从核心素养的视域来洞察深度学习的机制,有助于避免粗糙、僵化甚至错误的认识,合理、科学地诠释深度学习“黑箱”的内部过程.

深度学习的教学设计,需要在课堂活动形式和内容指向上做出根本性的调整.形式上的调整在于处理好课内与课外的关系,设计和实施学生有更多自主探究时间、问题空间和学习场域的探究活动.具有挑战性学习主题是探究活动的缘起和目标导向,是深度学习发生的必要前提.本例始于学生的一个疑问,教师步步设问,让学生深度认知椭圆在空间的几何性质,培养了学生的数学建模、直观想象、逻辑推理等核心素养.圆柱、椭圆、余弦线知识内在联系的证明,促进了学生高阶思维能力的发展,随着问题的逐步深入,学生产生了积极的情感体验.价值观对人们自身行为的定向和调节起着非常重要的作用,学生只有确立了正确的价值观,养成必备品格,才能实现持久地深度学习.

希尔伯特说:“数学科学是一个不可分割的有机整体,它的生命力就在于各个部分之间的联系.”充分认识数学这种内部统一性,并在教学中实践,对发展学生的核心素养至关重要.