核心素养导向的高中数学最值问题的教学思考

广东省东莞市南城中学(523077) 陈立

《普通高中课程标准(2017年版)》指出:数学学科核心素养是数学课程目标的集中体现,是具有数学基本特征的思维品质、关键能力以及情感、态度与价值观的综合体现,是在数学学习和应用的过程中逐步形成和发展的.核心素养是其他素养发展的基础,也是个人终身发展和可持续发展的根基.数学学科核心素养包括:数学抽象、逻辑推理、数学建模、直观想象、数学运算和数据分析.

最值问题就是在一定条件下求最大值或最小值,是高中数学教学的重要内容之一.多年来,高中数学竞赛题、高考题、模拟题、期中期末调研题等各级各类试题中,函数、不等式、数列、三角函数、立体几何、解析几何等模块的最值问题一直是命题的热点.解决好最值问题的教学对培养和发展学生的核心素养是非常必要的.东北师范大学校长(普通高中数学课程标准修订组长)史宁中教授在《高中数学核心素养的培养、评价与教学实施》一文中关于理想的教学过程描述如下:把握数学知识的本质、把握学生认知的过程;创设合适的教学情境、提出合适的数学问题;启发学生思考、鼓励学生与他人交流;让学生在掌握知识技能的同时,理解数学知识的本质;感悟数学的思想、形成和发展数学核心素养.这五个环节不是教学模式,也不要求在每一堂课上都实现,而是在进行整体教学设计时应当认真考虑的,是在进行整体教学实施时应当实践的.为此,本文从教材、试题中选取高中数学函数、不等式、数列、三角函数、立体几何、解析几何等模块的最值问题,通过寻找最值问题切入点和突破口,分析其功能来探索解决最值问题的教学思考.

1、高中数学竞赛试题中的最值问题

在“普及的基础上不断提高”方针指导下,高中数学竞赛方兴未艾.近几年来,高中数学联赛广东赛区选拔赛试题与全国卷高考真题命题的数学思想和方法贴近,为高考复习增添了新内容.为此,笔者认为在学生学习相近内容的时候,选取部分题目进行教学还是有必要的.

示例1(2016·全国高中数学联赛广东赛区选拔赛试卷第2题)若正数x,y满足x+3y=5xy,则3x+4y的最小值是____.

方法一切入点和突破口分析:该题可由基本不等式问题的解法切入,即把x+3y=5xy化为其突破口可以为然后求解;如果把x+3y=5xy化为y=问题为求3x+4y=3x+的最小值,其突破口为构造基本不等式(例如令t=5x-3,问题为求(t＞0)的最小值),或应用导数进行求解.

方法二切入点和突破口分析:该题也可由判别式法求最值切入,此时突破口是学生能构造出一个一元二次方程,即令3x+4y=k,因为x+3y=5xy,所以易知所以把并代入x+3y=5xy,整理得:15x2-5(k+1)x+3k=0.因为x是正数,所以Δ ≥0,解得(舍去),或k≥ 5,故(3x+4y)min=5.

题目的功能:通过该题的教学,主要提升学生的数学抽象、逻辑推理核心素养.

示例2(2015·全国高中数学联赛广东赛区选拔赛试卷第9题)在三棱锥S-ABC中,SA=4,SB≥7,SC≥9,AB=5,BC≤6,AC≤8,求三棱锥S-ABC体积的最大值.

在解答这道题时,一方面,考生要注意到几何体的形状是三棱锥不会改变,同时,△SAB的边SA=4,AB=5都是定值也不会改变;另一方面,考生也要意识到由于三棱锥S-ABC中有4条棱的棱长不确定,所以三棱锥的大小会改变,△SAB的面积也会改变;最后,对这些变与不变的关系认真梳理,应用等价转化的思想方法将问题化归为求三棱锥C-SAB体积的最大值.这样就可以完美的解答这个问题.

基于上面分析,该题的切入点如下:

(1)三棱锥的体积V=Sh.

(2)VS-ABC=VA-SBC=VB-SAC=VC-SAB.

(3)把三棱锥S-ABC的面△SAB看成底面才有利于求出三棱锥S-ABC体积的最大值,以△SAB所在平面为底面.

该如下有以下两点:

(1)求出△SAB面积的最大值.

观察图1,易知,当SB=7时,△SAB的面积取到最大值.△SAB面积的最大值的求法如下:SA·sin∠SAB=10sin∠SAB,因为∠SAB是△SAB的内角,所以 sin∠SAB=又因为-1＜所以0故

图1

(2)求出三棱锥C-SAB的高CO的最大值.

观察图2,得到CO≤SC,CO≤AC,CO≤BC.因为SC≥9,而BC≤6,AC≤8,所以CO≤AC,CO≤BC.以下考查CO与AC或BC重合后取其最大值的情况:

图2

(i)当CO=AC时,因为AC≤8,所以AC有最大值8,此时与BC≤6矛盾,不符合题意.

(ii)当CO=BC时,因为BC≤6,所以BC有最大值6,此时成立,符合题意.

故(VS-ABC)max=(VC-SAB)max

题目的功能:通过该题的教学,主要提升学生的数学抽象、逻辑推理、直观想象、数学运算等核心素养.教学选用这道题时,如果学生基础薄弱,可降低难度,把题目表述为:在三棱锥S-ABC中,SA=4,SB=7,SC≥9,AB=5,BC≤6,AC≤8,求三棱锥S-ABC体积的最大值.这样变式的话多数学生可独立完成,题目的功能基本相同.

2高考试题中的最值问题

对高考试题的教学和研究,其目的是精准把握教育教学方向、教学难度、教学深度和教学广度,是落实数学核心素养的重要方式.最值问题一直是高考的热点问题,以下以高考真题为例,谈谈自己怎样通过真题培养学生的核心素养.

示例1(2017·全国卷I理科·16)如图3,圆形纸片的圆心为O,半径为5cm,该纸片上的等边三角形ABC的中心为O.D,E,F为圆O上的点,△DBC,△ECA,△FAB分别是以BC,CA,AB为底边的等腰三角形.沿虚线剪开后,分别以BC,CA,AB为折痕折起△DBC,△ECA,△FAB,使得D,E,F重合,得到三棱锥.当△ABC的边长变化时,所得三棱锥体积(单位:cm3)的最大值为____.

图3

该题切入点如下:

(1)画出正三棱锥P-ABC(设D,E,F重合后为P)的直观图,如图4;

(2)PQ+OQ=5;

(3)引入变量,有多种方法,但是用引入的变量表示VP-ABC的难度不同,相对比较容易的是设OA=2x则有OQ=x,PQ=5-x,从而

图4

该题的突破口是求VP-ABC=VP-ABC的最大值,笔者认为快且准的解法还是应用基本不等式,即:=155(当且仅当x=2时取等号),故(VP-ABC)max=(

题目的功能:通过该题的教学,主要提升学生的数学抽象、直观想象、数学运算核心素养.

该题的题干与教材必修2第37页B组第4题相近,题目如下:

一块长为10cm的正方形铁片按如图5所示的阴影部分裁下,然后用余下的四个全等的等腰三角形加工成一个正四棱锥形容器,试把容器的容积V表示为x的函数.

图5

图6

因为学生在学习必修二时还没有学习三次函数最大值的求法,所以这道题仅要求学生把容器的容积V表示为x的函数.当学生学习了三次函数最大值的求法之后,作为教师有没有把教材上的这个题目再找出来,让学生应用有关知识求容器的容积V的最大值,值得我们反思.

示例2(2018·全国卷I理科·12)已知正方体的棱长为1,每条棱所在直线与平面α所成的角都相等,则α截此正方体所得截面面积的最大值为( )

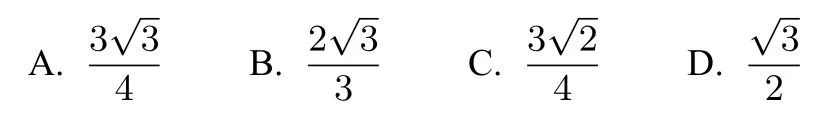
这是2018年全国高考I卷(理科数学)选择题的压轴题,因为该题是求“每条棱所在直线与平面α所成的角都相等”,所以该题的切入点就是把正方体的棱按与平面α所成的角相等分为三类,易得结论,切入点也是该题突破口.

如图7,当平面α截正方体所得到的截面为边长为的正△ABC时,所得的截面面积最大,最大值为:故选D.

图7

题目的功能:通过该题的教学,主要提升学生的数学抽象、直观想象核心素养.

示例3(2018·全国卷I理科·16)已知函数f(x)=2sinx+sin2x,则f(x)的最小值是____.

这是2018年全国高考I卷(理科数学)填空题的压轴题.如果把该题看成“函数的最值与导数”这一类问题,则该题的切入点如下:

(1) 求导,即f′(x)=2cosx+2cos2x=4cos2x+2cosx-2.

(2)判断f′(x)的符号.

显然,f′(x)=2(2cosx-1)(cosx+1),其中 cosx∈[-1,1].因为cosx∈时,f′(x)≤ 0,cosx∈时,f′(x)＞0.

该题的突破口就是:判断cosx时,f(x)取得极小值吗?f(x)的最小值与cosx=有什么关系?如果懂这样思考,得到并不难.

该题的功能:通过该题的教学,主要提升学生的逻辑推理核心素养.

当然,该题也可以利用基本不等式求解,切入点如下:f(x) = 2sinx+sin2x=

突破点是:

(1+cosx)2sin2x(当且仅当cosx取“=”). 所以从而得到.如果按这样安排该题的教学,那么通过该题的教学,可提升学生的数学抽象、逻辑推理核心素养.

希望本节所列的几个问题能起到抛砖引玉作用,近几年全国高考数学试题中还有许多最值问题值得我们执教者深入研究.

3、模拟试题、调研试题中的最值问题

近几年全国各地的高三数学模拟题、东莞市的调研题等都编制了一些很高水平的最值问题,本文仅选几例加以研究.

示例1 (2017-2018广州一测·理科数学·12)设函数f(x)在ℝ上存在导函数f′(x),对于任意的实数x,都有f(x)+f(-x)=2x2,当x＜0时,f′(x)+1＜2x,若f(a+1)≤f(-a)+2a+1,则实数a的最小值为( )

该题的切入点如下:

定义域关于原点对称的函数都能拆分为一个奇函数和一个偶函数的和.基于这个结论可设f(x)=g(x)+h(x),其中g(x)为偶函数,h(x)为奇函数,x∈ℝ,那么f(-x)=g(x)-h(x),又f(x)+f(-x)=2x2,从而f(x)=x2+h(x).

该题的突破口如下:

利用f′(x)+1＜2x得f′(x)＜2x-1,而f′(x)=2x+h′(x),所以h′(x)＜-1,基于此结论可知h(x)=kx+b(k＜-1,b为常数).从而得到f(x)=x2+kx+b,则f(a+1)≤f(-a)+2a+1可化为:(a+1)2+k(a+1)+b≤(-a)2+k(-a)+b+2a+1,即k(2a+1)≤0,又k＜-1,解得故

题目的功能:通过该题的教学,主要提升学生的数学抽象、逻辑推理核心素养.

示例2(2017-2018广州二测·理科数学·11)体积为的三棱锥P-ABC的顶点都在球O的球面上,PA⊥平面ABC,PA=2,∠ABC=120°,则球O的体积的最小值为( )

该题的切入点如下:

(1)利用PA⊥平面ABC和∠ABC=120°,先画出草图(如图8),然后由已知求出S△ABC=

(2) 由S△ABC=及∠ABC=120°可得:AB·BC=6,然后应用余弦定理,得:AC2=AB2+BC2+AB·BC≥AB·BC=18,所以 (AC)min=从而得到△ABC的外接圆半径有最小值

图8

该题的突破口如下:

将三棱锥P-ABC延展成直三棱柱,如图9,易知球心O到底面ABC的距离为定值1,求三棱锥P-ABC外接球体积的最小值就是求球O半径R的最小值,所以故选 B.

图9

题目的功能:通过该题的教学,主要提升学生的逻辑推理、直观想象核心素养.

示例3(2017-2018深圳一模·文科数学·16)如图10,在△ABC中,∠ABC=90°,AC=2BC=P是△ABC内一动点,∠BPC=120°,则AP的最小值为____.

图10

该题的切入点是:根据∠BPC=120°,BC=以及正弦定理可知△BPC的外接圆是确定的,其外接圆半径为1.

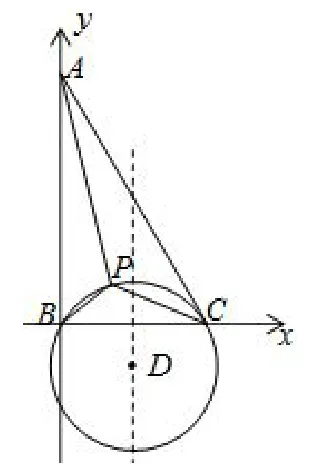
图11

该题的突破口是:建立平面直角坐标系,如图11所示,求出△BPC外接圆圆心D的坐标将求AP的最小值转化为求A到圆D的劣弧BPC(不包括端点)上任意一点距离的最小值,故(AP)min=AD-1=1.

题目的功能:通过该题的教学,主要提升学生的数学抽象、逻辑推理直观想象核心素养.

示例4(2015-2016东莞市高三第一学期期末调研·理科数学·16)如图12,在凸四边形ABCD中,AB=1,BC=AC⊥CD,AC=CD.当∠ABC变化时,对角线BD的最大值为___.

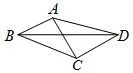
图12

该题的切入点如下:

设∠ABC=θ,θ∈(0,π),建立如图13所示的平面直角坐标系,则A(cosθ,sinθ),C(0).

图13

该题的突破口是:由Rt△AEC～=Rt△CFD, 得所以故(BD)max=+1.

题目的功能:通过该题的教学,主要提升学生的数学抽象、数学运算核心素养.

示例5(2016-2017东莞市高三第一学期期末调研·理科数学·16)在△ABC中,∠ACB=120°,D是AB上一点,满足∠ADC=60°,CD=2,若CB≥则∠ACD的最大值为____.

该题的切入点是:依题意画出图形,如右图14,将问题转化为“求∠BCD的最小值”,这也是该题的突破口.过程如下:

图14

在△BCD中,由 正 弦 定 理,得所以BC=

因为 0° ＜∠BCD＜60°,所以60°-∠BCD≤ 45°,即∠BCD≥ 15°,所以 (∠BCD)min=15°,故 (∠ACD)max=120°-15°=105°.

题目的功能:通过该题的教学,主要提升学生的数学抽象核心素养.

该题的突破口是:把求|PQ|的最小值化为求上的点到直线y=x距离最小值的2倍,进而化为求曲线的与y=x平行的切线与y=x距离的2倍,此时只需求出切线方程y=x+1-ln2,然后由平行线间的距离公式得|PQ|min=

题目的功能:通过该题的教学,主要提升学生的数学抽象核心素养.

4、结束语

随着《普通高中数学课程标准(2017年版)》的出版发行,数学学科核心素养正式进入高中数学课程.高中数学教学要以发展学生数学学科核心素养为导向,以学生发展为本,培养学生的科学精神和创新意识,提升学生数学学科核心素养.本文重点研究了最近几年高考真题、模拟题和调研题中的选填题压轴题的教和学,旨在探索核心素养导向的高中数学的教与学.以上所选最值问题综合性较强、思维要求较高,文中分析了这些问题的切入点和突破口,并且对这些题目的教学主要提升学生的哪些核心素养作简要描述.笔者认为把这个难度的问题教好是发展学生核心素养的重要途径,把这个难度的问题教好也必将带来教学成绩的提高.