谈谈数学例题学习前的准备

广东省佛山市顺德区乐从镇沙滘初级中学(528315) 刘福斌

在数学教材中,每当我们学完某一章节的知识点后,总安排一道相应的例题,让学生学习如何运用相应的知识解决问题.学好一个例题往往能掌握解决与该知识点相关的问题的方法,因此,可以说例题的学习是新课学习的关键.怎样学习例题是一个值得我们探讨的问题.我们知道,例题学习并不是把例题简单地一读了之,或是机械地记忆解题过程,如果想把学习例题的效率发挥到最好,我们在学习例题前就需要作好充分的准备.本人结合平时的教学,在此谈谈自己的一些做法:

一、教师可以根据实际情况,可以大胆的对例题题目进行适当的改造.

一般来说,数学教材上的例题是具有代表性的典型题目.虽然教材是专家们编写的,但他们多数并不是第一线的教师,所以他们在教材中设计的例题有时难免会缺乏生活味,没有现实的情境.因此,我们在进行新授课的教学时,可以对教材的例题先进行分析,看其是否富有丰富生活气息,若内容过于枯燥,教师可以结合学生生活实际改编教材例题,使学生将更多的视角投向现实生活.例如在学习“行程问题”的应用题时,例题里通常会有“从A地到B地60公里……”等类似的较为空洞的例子,我们可以把它改为“从大良镇到乐从镇约50公里……”等等,这样将更贴近现实生活,从而可提高学生学习的积极性.又如:在学习以下的例题:我国自2011年9月1日起,个人工资、薪金所得税征收办法规定:月收入不超过3500元的部分不收税;月收入超过3500元的部分征收3%的所得税……如某人月收入超3860元,他应缴纳个人工资、薪金所得税为:

(3860-3500)×3%=10.8(元)

(1)当月收入超过3500元而又不超过5000元时,写出应缴纳个人工资、薪金所得税y(元)与月收入x(元)之间的关系式;

(2)某人月收入为4160元,他应缴纳个人工资、薪金所得税多少元?

(3)如果某人本月缴纳个人工资、薪金所得税23.4元,那么此人本月工资、薪金收入是多少元?”

此题对学生来说比较枯燥无味,但我们可以将第(2)问改成:我校的一位宿管人员的月收入为3760元,她应缴纳个人工资、薪金所得税多少元?第(3)问改成:如果数学老师本月缴纳个人工资、薪金所得税30.2元,那么请帮我算算我本月工资、薪金收入是多少元?

由于学生对自己身边的人,尤其是老师的工资收入特别好奇,在好奇心的驱使下他们自然会对此题产生浓厚的兴趣,从而积极去完成这道题.

二、教师可以用与例题有关的知识的进行铺垫,突破学习例题的难点.

我们在平时的例题学习当中,或多或少的总会碰到一些的“疙瘩”.为了让学生能顺利地学好例题,教师可以在学习前,用与例题有关的知识的进行铺垫,从而突破学习例题的难点.例如,九年级数学中有这样的例题:

某种衬衫平均每天可销售40件.每件盈利20元.调查发现:若每件衬衫降价1元.每天可多销售10件.

(1)如果每天盈利1350元.每件应降价多少元?

(2)每天盈利可否达到1500元?若能,请计算每件衬衫应降价多少元?若不能.请说明理由.

商品销售问题是应用题的难点,为更好地解决这类问题,必须让学生理解商品销售中的“六个术语”,并掌握“二个数量关系”.

其中“六个术语”是:

1.商品的进货价:指商店从厂家购进商品时的价格;

2.商品的定价:商品销售时所标出的价格;

3.商品的售价(或成交价):商店销售商品时的售出价;

4.商品的原价:商店原来销售商品的售出价

5.利润:商店销售商品时所赚的钱;

6.销售量:销售商品的数量

“两个数量关系”:

1.商品的利润=商品的售价-商品的进价;

2.商品的总利润=每件商品的利润×销售量;

当学生理解了这些术语和关系后,才能更好会读懂题目,从而完成例题的学习.

三、教师要尽可能掌握解决例题的方法,提倡例题一题多解,培养学生的创新思维能力.

我们在学习例题时,往往会发现解决例题的方法不止一种,如果我们在备课时没有尽可能掌握解决例题的方法,那么就有可能忽略了一些较有创意的解法,这样便会不利于学生创造思维能力的培养.如:北师大版八年级数学(上册)P242的例2:

某长途汽车客运站规定,乘客可以免费携带一定质量的行李,但超过该质量则需购买行李票,且行李费y(元)是行李质量x(千克)的一次函数.现知李明带了60千克的行李,交了行李费5元;张华带了90千克的行李,交了行李费10元.

(1)写出y与x之间的函数表达式;

(2)旅客最多可免费携带多少千克的行李?

多数学生利用待定系数法求函数表达式解决第(1)题时.但我在巡堂时发现有部分学生用了其它两种不同的方法.一种是设每千克行李费x元,免费携带y千克的行李,然后列出方程组,求出x、y的值,从而找出答案;另一种是利用小学算术的方法,先求出超过免费质量的行李每千克的行李费:元,5元的可携带行李质量是千克,再求出免费行李的质量:60-30=30千克.于是(1)及(2)的答案便一目了然.由于在备课时我有尝试过这两种方法,所以我马上肯定他们的方法是对的,并对他们及时作出了表扬,并他们向全班同学作了推介,并提倡他们要一题多解.

四、教师可以把例题进行适当的变形,学生对例题学习的理解真正达到融会贯通.

在平时教学当中,我们常发现这样的问题:课堂上教师讲了一道例题,当时学生相应的题目时做得不错,但当让他们来做稍加变化的题目,很多学生便无从下手了.这说明学生可能处于学习“思维定势”,只是单纯地依赖模仿与记忆,不会变通.要改变这一状况,必须培养学生的数学思维能力.而要培养学生的数学思维能力,可从例题变式教学入手.例如下题:

例如图1,已知:在平行四边形ABCD中,点E、F在AC上,AE=FC,四边形BFDE是平行四边形吗?请说明理由.

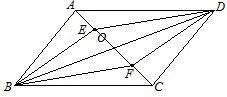
图1

我们可以适当把它变形为:

补例1如上图,已知:在平行四边形ABCD中,点E、F在AC上,E、F分别是AO、CO的中点,四边形BFDE是平行四边形吗?请说明理由.

补例2如上图,已知:在平行四边形ABCD中,点E、F在AC上,四边形BFDE是平行四边形吗?请说明理由.

补例3如上图,已知:在平行四边形ABCD中,点E、F在AC上,请添加一个条件__,使四边形BFDE是平行四边形.

我们通过对例题加以适当变形,学生可以从多角度,多层次,多结论等方面去认识知识,思维活动的质量也得到了提高,使学生对例题学习的理解真正达到融会贯通.

五、教师可以引导学生在学习新课前先自学例题,让学生加深对例题的理解.

在新课学习中,有些题目比较难,在课堂中留给学生思考的时间可能不够,那么我们可以让学生先提前预习,尝试自己先做例题,如果确实做不了,那么让学生带着问题去听课,那么教学效果才不会打折扣.如在学习以下例题:

用反证法证明:一个三角形中不能有两个角是直角.

学生平时学习的证明题都是从正面去完成的,但这一次要从反面去证明,学生可能会无所适从,我们可以让学生先反证法的定义,理解反证法的操作过程后,让学生自行大胆尝试完成证明,不管学生写成什么样,我们都可以让学生在课堂上大胆展示出来,然后,老师再引导学生完善证明过程,并总结步骤,这样教学效果就会得到保证.

当然,例题学习前的准备还有许多,比如学习工具的准备、学习氛围的创设等等.如果我们想把例题的学习落实好,让新课的学习质量得到保证,我们平时就要多做功课,多做准备.只有勇于尝试,勤于思考,善于总结,我们的课堂才会更加精彩,学生才会更加喜欢我们的课堂,我们的教学水平才会不断提高,教学效果才会越来越好.