对角线互相垂直的四边形的性质之一

北京师范大学出版集团(100875) 岳昌庆

菱形及正方形的两条对角线互相垂直,那么对角线互相垂直的四边形都有哪些性质呢?

(1)对角线互相垂直的四边形的面积等于两对角线长乘积的一半.

(2)顺次连结对角线互相垂直的四边形的四边中点,所得四边形为矩形.

(3)对角线互相垂直的四边形,一组对边的平方和等于另一组对边的平方和.

(4)如果四边形一组对边的平方和等于另一组对边的平方和,那么它的对角线互相垂直.

(5)若圆内接四边形对角线互相垂直,则由对角线交点所引一边之垂线必平分其对边.

还有其他性质,不再一一列举.

性质1-2的证明显然,也屡次出现在中考、高考数学试题中,本文不再赘述.仅就性质3-4谈一点趣用(性质5,笔者也有专文论述,此处限于篇幅,不涉及)

例1已知:如图1,四边形ABCD中,AC⊥BD于O.求证:AB2+CD2=AD2+BC2.

图1

简证在Rt△AOB中,AB2=AO2+BO2,在Rt△COD中,CD2=CO2+DO2.所以AB2+CD2=AO2+BO2+CO2+DO2,同理AD2+BC2=AO2+BO2+CO2+DO2,所以AB2+CD2=AD2+BC2.

评注对角线互相垂直的四边形,一组对边的平方和等于另一组对边的平方和.

试问:上述命题的逆命题是否正确?答案是:逆命题也成立,即

例2已知:如图2,四边形ABCD中,AC,BD交于O且AB2+CD2=AD2+BC2.求证:AC⊥BD.

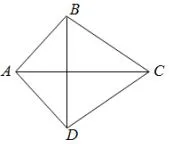
图2

简证作AE⊥BD于E,作CF⊥BD于F,由勾股定理得AB2+CD2=AE2+BE2+CF2+DF2,AD2+BC2=AE2+DE2+BF2+CF2,由已知AB2+CD2=AD2+BC2可得BE2+DF2=DE2+BF2,即DF2-DE2=BF2-BE2,(DF+DE)(DF-DE)=(BF+BE)(BF-BE),-(DF+DE)FE=(BF+BE)FE,所以,2BD·FE=0,又BD/=0,所以FE=0,即F,E重合,所以AC⊥BD.

评注(1)如果四边形一组对边的平方和等于另一组对边的平方和,那么该四边形的两对角线必互相垂直.

(2)本质上本题证法是同一法.

(3)高一学习了余弦定理、向量、平面解析几何中的解析法证明后,均可轻松获证.

例3(1999年中考上海市卷第20题2分压轴题)(2000年中考山东省卷第18题3分)四边形ABCD中,如果____,那么这个四边形的对角线AC和BD互相垂直(只需填出使结果成立的一种情况即可).

解(1)四边形ABCD是正方形;

或(2)四边形ABCD是菱形;

或(3AB=AD,BC=CD;

或(4)AB2+CD2=AD2+BC2,等

评注(1)(2)是考生常见答案,(3)也有相当一部分考生能答得上,能答得出(4)的几乎是凤毛麟角了.