学贵在疑,疑贵于思

浙江省宁波市镇海区尚志中学(315100) 蔡晓娜

题目呈现如图1,在△ABC中,∠BAC= 90°,AB=AC,点D在BC上,且BD=BA,点E在BC的延长线上,且CE=CA.

图1

(1)求∠DAE的度数.

(2)如果把题干中的“AB=AC”的条件舍去,其余条件不变,那么∠DAE的度数会改变吗?并说明理由.

(3) 如果把题干中“∠BAC= 90°”的条件改为“∠BAC＞90°”,其余条件不变,那么∠DAE的度数与∠BAC有怎样的大小关系?并说明理由.

分析与简答此题出现在浙教版八年级上《2.6直角三角形》的课外练习中,考查了等腰(等腰直角)三角形的性质,三角形外角性质知识点.

(1)问中,根据等腰直角三角形的性质可得∠B=∠ACB=45°,再根据等边对等角的性质求出∠BAD=∠BDA=67.5°,∠E=∠CAE=22.5°,从而得到∠DAE=∠BDA-∠E=45°.

(2)由BD=BA可得∠BAD=∠BDA=(180°-∠B),由CE=CA可得∠E=∠CAE=∠ACB=(90°-∠B),从而得到∠DAE=∠BDA-∠E=(180°-∠B)-(90°-∠B)=90°-∠B-45°+∠B=45°,即∠DAE的度数不变.

(3)由BD=BA可得∠BAD=∠BDA=∠B),由CE=CA可得∠E=∠CAE=从而得到∠DAE=∠BDA-∠E=90°-∠B,因为∠BAC=180°-2∠B,所以∠DAE=

此题三问设置层层递进,由易到难,由于(1)中各个角度都可以算出来,故学生回答较好,而(2)和(3)中无法算出具体的角度,需要设元,即所有的角度都可以用含∠B的代数式来表示,对于初二的学生非常害怕这样的运算,或者说还没有含参运算意识,所以正确率不高.

疑问与对策疑问1:第(3)问中“∠BAC＞90°”这个限制条件在解答的过程中没有用到,那为什么还要加这个限制条件呢,直接把“∠BAC=90°”这个条件去掉就行了.

（26）下滅妖氛：邪氛侵氣，妄逞收平。（《太上說玄天大聖真武本傳神呪妙經註》卷三，《中华道藏》30/554）

对策:师:当∠BAC＞90°时,图形画出来是这样的(如图2),那么当∠BAC＜90°时,图形又是怎么样的呢?请同学们画一画.

图2

图3

生2:如图3.

生3:如图4.

生4:图3可以,图4不满足“点D在BC上”这个条件.

师:同样都是∠BAC＜90°,什么时候满足“点D在BC上”这个条件?

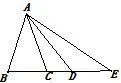
图4

生5:当 60°≤∠BAC＜90°时才满足,若∠BAC＜60°,点D在BC的延长线上.

师:图3此时有∠DAE=∠BAC的结论吗?

生:有,证明过程跟(3)的一样.

生:也有,证明过程跟(3)的一样.

师:经过我们的探究,其实此题可以这么改:先把题干中的“点D在BC上”这个条件改为“点D在射线BC上”,然后第(3)问改为“如果把题干中“∠BAC=90°”的条件去掉,其余条件不变,那么∠DAE的度数与∠BAC有怎样的大小关系?并说明理由.”只不过同学们在解答的过程中,需要分类讨论.

疑问2:题中的(2)(3)都是在(1)的条件下提出的,而本身之间是独立的,没有联系,是否可以把“AB=AC”和“∠BAC=90°”这两个条件同时去掉?

对策:师:去掉这两个条件,请同学们画出图像.

生6:如图5.

生7:如图6.

图5

图6

师:画出来也是可以分成点D在线段BC上或者在BC的延长线上,那么此时有∠DAE=∠BAC的结论吗?

生8:由BD=BA可得∠BAD=∠BDA=(180°-∠B),由CE=CA可得∠E=∠CAE=∠ACB,从而得到∠DAE=∠BDA-∠E=(180°-∠B)-∠ACB=90°-∠B-∠ACB,因为∠BAC=180°-∠B-∠ACB,所以∠DAE=∠BAC.

疑问3:“点D在BC上”都可以改成“点D在射线BC上”,那么能否改成“点D在直线BC上”呢?

对策:师:我们只要考虑点D在射线BC的反向延长线时,请同学们画出图像并思考此时∠DAE和∠BAC又有怎样的关系?

生9:如图7.由题意得∠D=∠E=所以∠DAE=而∠BAC=180°-∠ABC-∠ACB,所以∠DAE=

图7

疑问4:既然“点D在直线BC上”了,那么点E能否在直线BC上?

对策:师:当点E在直线BC上时,除了上面讨论的这几种情况外,还有哪些可能?请画图.

生10:如图8.由BD=BA可得∠BAD=∠BDA=由CE=CA可得∠CEA=∠C),从而得到∠DAE=180°-∠BDA-因为∠BAC=180°-∠ABC-∠ACB,所以∠DAE=90°-

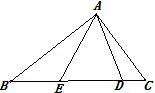
图8

几点思考

一、在质疑中进步

常听教师抱怨:“现在的学生,教了多少遍都不会”,“教过了才会,稍微变形一下就不会”等等.目前的课堂教学,不管是讲授式还是小组合作式,为了完成教学目标,教师的预设往往过强,学生所谓的生成都是“被生成”.明代学者陈献章说过:“学贵有疑,小疑则小进,大疑则大进.”要想学生能在学习中有较大的进步,则需要学生能有质疑的精神,要让学生会于质疑,敢于质疑.所以教师在平时的教学过程中应当营造和谐的氛围去引导学生去质疑,质疑题目,质疑老师,质疑课本.

二、在质疑中发散

在学习过程中,若学生都是“被思考”,那么长久以往,学生的思维就会僵化,越来越离不开老师的“预设”,缺少独立思考的能力,就会出现题目做过了,老师讲过了,那还是可以做做的,遇到新的问题和情景却一脸茫然,无从下手的现状.古人云:“学起于思,思源于疑.”可见质疑对于学生的思维发散是多么的重要,所以教师应该努力要让学生善于质疑,只要有质疑了,那么才会有接下去解决质疑的动力,学生才会去思考,思维才会不断运转.正如上面的例子中可以发现,学生对题目中的所谓的“多余条件”有了质疑,才会引出接下来的一串的质疑和思考.

三、在质疑中创新

《义务教育数学课程标准(年版》中,对学生的培养目标在具体表述上做了一定的修改,提出了“四基”和“四能”.所谓“四能”,指的是发现问题和提出问题的能力、分析问题和解决问题的能力.现在的学生在题海战术中,分析问题和解决问题的能力往往比较突出,欠缺的是发现问题和提出问题的能力.爱因斯坦说:“提出一个问题往往比解决一个问题更为重要”.因为解决问题,也许仅是技能而已,而提出新的问题新的可能性,从新的角度去看旧的问题,却需要创造性的想象力,而且标志着科学的真正进步.所以教师应该让学生乐于质疑,在质疑中得到学习数学的乐趣,在质疑中创新.在上述例子,学生从对条件“∠BAC＞90°”的质疑,经老师的引导和启发,自己的动手操作,又产生了新的质疑,把此题的结论推广到了更一般化,可以说是对原题的创新.

总之,质疑可以使教师的教学更有的放矢,可以引导学生深入理解课文,可以促进学生主动探究,勇于发现,可以激活学生的思维.越是敢于质疑的学生,其主体作用越能得到充分的发挥.所以老师们,请放手让学生质疑吧!