随机效应模型的复合分位数回归估计

罗登菊，戴家佳，罗兴甸

(贵州大学 数学与统计学院，贵州 贵阳 550025)

随机效应模型的一般形式为：

(1)

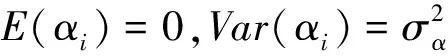
模型(1)的主要优点在于，在一定条件下提供了对个体进行统计推断的可能性。为了解决此模型估计的参数估计问题，大部分的文献通过普通最小二乘和加权最小二乘等方式来解决此问题，举例说，最小二乘估计计算简单，其得到的结果拥有令人满意的表达式，尤其是在误差项遵循常态分布的前提下，最小二乘估计是有效的，而且是一致最小方差无偏估计。但是实际数据往往不满足方差相等、独立并服从正态分布等严苛条件。随着互联网的高速发展以及各种行业之间相互影响，我们所面临的数据维度不仅大还结构复杂，通过最小二乘估计无法满足现阶段所需理想的统计结果。

于是，加拿大学者KOENKER提出了一种回归估计，就是分位数回归估计，目的是为了摆脱最小二乘估计的局限性，更广泛的将中位数回归应用于所有的分位数中。使用条件分位数来进行建模，使最小二乘估计最小化平方误差的思想变为最小化加权的绝对误差，该方法可以刻画解释变量随响应变量变动的大体特征，呈现响应变量在不同分位点下的条件分布函数。分位数回归有众多优势，它既不需要误差项服从正态分布，也对异常值不敏感，甚至可以拟合响应变量任何分位点的回归方程，因此具有很好的稳健性，在各个模型的估计中被广泛运用，例如，WU[1]在研究单指标模型的估计问题时，使用了分位数回归估计；YANG[2]应用分位数回归研究了变系数单指标模型的参数估计和变量选择问题；KONEKER[3]更是史无前例的将分位数回归方法应用到纵向数据中，并指出对于固定效应模型，在进行分位数回归时，将L1惩罚项加入到目标函数中，并在估计未知参数时使用惩罚函数法；WANG[4]在探究面板数据中固定效应模型的经验似然估计值的过程中，分位数得分函数被平滑经验似然估计过程所替代，从而得到经验对数似然率和极大经验似然函数。CANAY[5]在去除面板数据模型中的固定效应时，采用了一种简洁的数据转换，之后利用分位数回归预估模型中的参数，同时还验证了该估计量的一致性和渐进正态性；KATO[6]以与非线性面板数据的研究相似为前提，研究面板数据下固定效应分位数回归模型估计的一致性和渐进正态性条件，得出一个结论，即参数估计量的一致性；何晓霞等[7]利用分位数回归研究了纵向数据下回归模型的参数估计和变量选择问题。根据以上文献得知，即便分位数回归可以融合多条曲线，但在实际问题中却存在部分分位点偏离过大的问题，因此，ZOU和YUAN[8]通过综合考虑将多个分位点，第一次提出了复合分位数回归估计，得到了回归系数β一个精度更高的估计。王琪锋[9]将复合分位数回归应用到线性时间序列数据中；王江峰[10]在左截断数据下研究了非参数模型的复合分位数回归估计；吕亚召[11]利用复合分位数回归研究了部分线性单指标模型的变量选择问题；JIANG[12]将复合分位数回归应用到DTARCH模型中；JIANG[13]将复合分位数回归应用到具有重尾自相关误差的线性模型中；CHEN[14]利用复合分位数回归估计半参数模型中的未知函数与参数；JIANG[15]将加权复合分位数回归估计引入到部分线性变系数模型中；徐洁和杨宜平[16]首次将复合分位回归应用到纵向数据中，研究了固定效应模型的复合分位数回归估计，在一定正则条件的前提下，证明了该估计的大样本渐近正态性质。

本文基于复合分位数回归方法研究了纵向数据下随机效应模型的参数估计，首先，给出该估计的定义与在该模型下的目标函数；再次，证明了在随机效应模型下的复合分位数回归估计的大样本渐近正态性质；最后，通过模拟研究了该估计量的有限样本性质，同时，与最小二乘估计、中位数估计结果的精度做比较。

1 模型和估计方法

我们将模型(1)改写为：

(2)

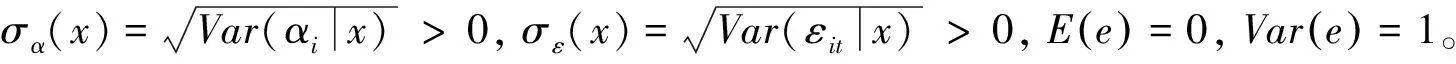
其中

ρτk(s)=τksI(s≥0)+(1-τk)sI(s<0)。

设ck是e的τk分位点，记σ=σα(x)+σε(x)，定义σ的估计为[15]：

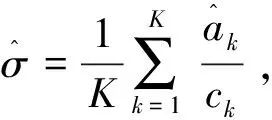
(a)

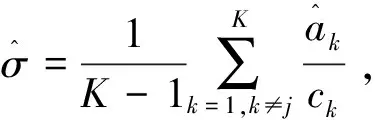
(b)

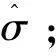
2 渐近性质

为更好的得到参数β估计的大样本性质，给出以下正则条件：

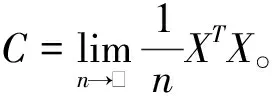
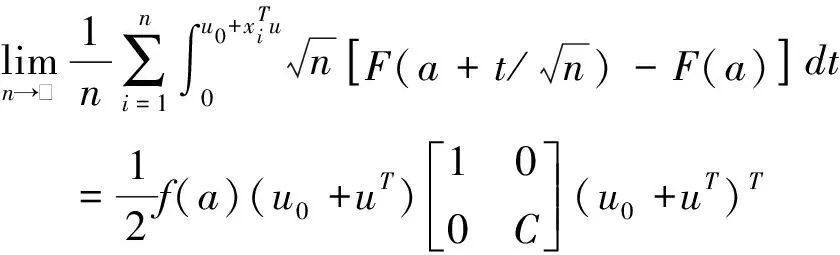
其中

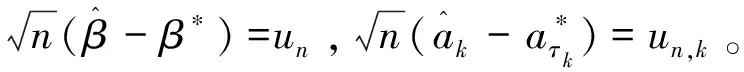
(c)

根据KNIGHT[17]

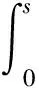
有

ρτ(r-s)-ρτ(r)=s(I(r<0)-τ)+

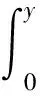
因此，Ln可表示为

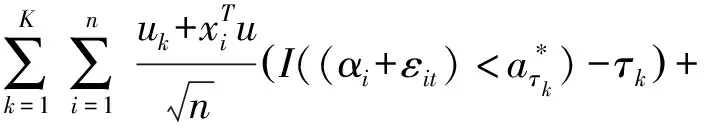
其中

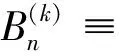
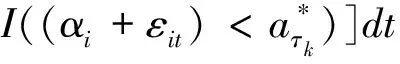
根据Cramer-Wald理论和中心极限定理可得，对任意∑，有

有

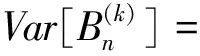
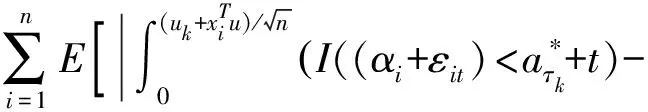
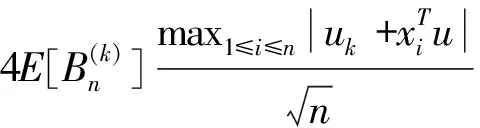
→0。

因此

因此可以得到

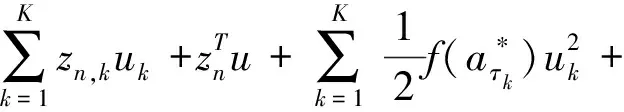
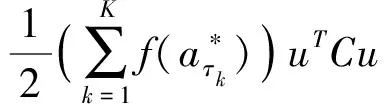
由于Ln是凸函数，有

其中

因此

证毕。

3 模拟研究

在模拟研究中，主要进行模拟研究来验证所提方法的有限样本表现。

考虑如下随机效应模型(3):

yit=xitβ+αi+εit

(3)

其中i(i=1,2,…,n)和t(t=1,2,…,T)分别表示个体和观测时间，观测周期取3，xit服从于标准正态分布N(0,1)，考虑了模型误差项εit分布服从3种分布的情形，包括：标准正态分布N(0,1)；自由度为3的t分布t(3)以及标准柯西分布c(0,1)。

取样本量n=50,100,200分别模拟500次。用传统最小二乘(LS)、中位数回归(QR0.5)以及复合分位数回归(CQRk)，复合分位数回归的分位点K值设定为5、9、 和19。在检验估计精度的好坏上，选择了偏差(Bias)、均方根误差(RMSE)以及标准差(SD)三个指标参数来衡量。模拟结果见表1，指标计算如下：

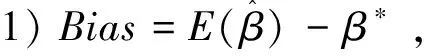
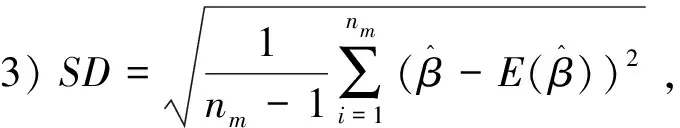
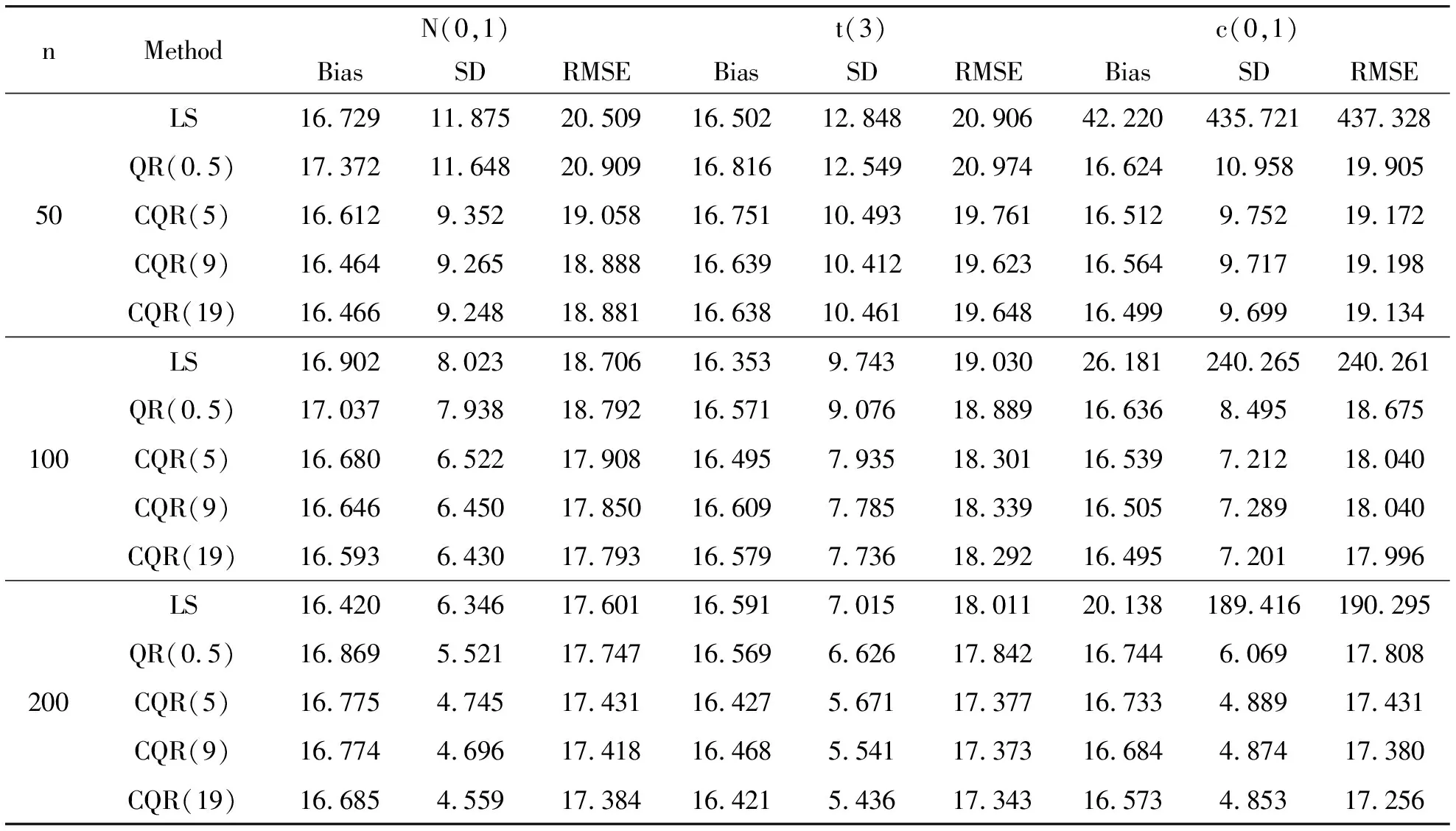
表1 参数估计的Bias,SD,RMSE模拟结果Tab.1 Parametric estimation of Bias, SD, RMSE simulation results 10-2

由表1可知：

(1)当样本量相同时，三种估计方法的精度比较，复合分位数回归的Bias、SD以及RMSE都是最优的。当模型误差服从N(0,1)时，最小二乘回归和中位数回归、复合分位数回归的结果之间的相近程度很高，甚至于最小二乘回归所表现出来的结果更优；然而在误差项服从非正态分布时，复合分位数回归和中位数回归表现更好，而最小二乘回归的表现却并不是很好。特别是在误差服从c(0,1)时，中位数回归估计和复合分位数回归估计的表现优于最小二乘回归，此时的最小二乘估计却完全无法发挥效用。就估计结果的精度而言，复合分位数回归精度高，而中位数回归则略逊一筹。

(3)通过对复合分位数回归中K的取值不同，可以发现大多数情况都是K=19时，参数的估计精度更高，说明随着分位数个数的增加，复合分位数回归估计的表现更好，从模拟结果可以看出，K=19与K=9时的结果相差不大，但是K=19会远远的增大计算量，所以在应用中选择K=9。

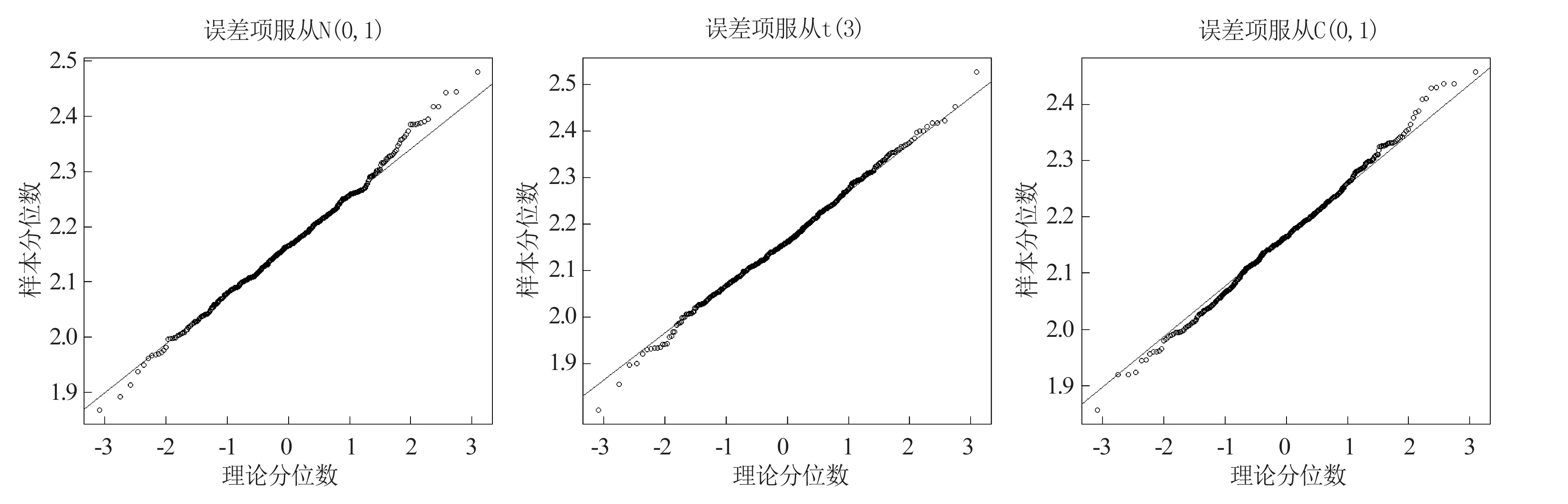
图1 参数估计的Q-Q图Fig.1 Q-Q graph of parameter estimation

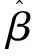
4 结论

本文通过引入了复合分位数回归方法来估计随机效应模型的未知参数，得出的结论如下：

(1)在随机效应模型中，利用复合分位数回归估计来估计未知参数，满足大样本性质。

(2)在样本量相同的情况下，复合分位数回归比中位数回归和均值回归的精度高，效果优。随着样本量的增加，所有估计的精度均增加，但是复合分位数回归效果最好。随着复合分位点的增加，复合分位数回归的精度也随着增加。