单分位数方法对时间序列尾指数变点检测及应用
周江娥,胡 尧,2*,商明菊
(1.贵州大学 数学与统计学院,贵州 贵阳 550025;2.贵州省公共大数据重点实验室,贵州 贵阳 550025)
通常,我们将样本用一个分布或者模型进行刻画,变点则是指其分布、模型或其参数突然发生改变之点称为变点,通过变点检测可以分析出造成该变点的原因,从而找到有效的解决办法。自Page以来,大量的研究都致力于变点分析这一理论及其在各个领域中的应用[1]。在现有的方法中,Cusum检验因其在实际应用中的易用性而长期流行,与似然法相比,原序列真实分布未知情况可使用Cusum方法。例如文献[2,3]。在金融和生物统计中,数据常具有尖峰厚尾的性质,尾指数是描述此特征的一个重要指标。实际应用中,大多数文献关注的是导致极端事件发生变化的均值或方差,但尾部的变化(即尾指数变化)会导致更多的极端事件。
极端现象的统计建模和分析是非常关键的,因为灾害和恐慌事件(如洪水、大地震和股市崩盘)的潜在风险可以事先确定,从而使它们得到充分的管理或预防。在此基础上,研究极值理论中的变点检验问题,特别是由于尾指数代表分布的肥胖程度,并确定了样本最大值等极值渐近分布的形状,因此本文重点研究分布尾指数的变点检测。尾指数估计问题是几十年来统计、金融、水文[4]、可靠性和通信工程中的一个核心问题。Quintos et al.和Kim et al.发展了一种检测分布尾指数参数变点的方法,这两种方法都是基于Hill的尾指标估计,都是针对厚尾分布而进行的[5,6]。根据Lee et al.提出的检验程序,考虑尾序过程,构造Cusum检验并证明尾序列过程在假设尾指数保持为常数的原假设下弱收敛于布朗运动[7]。
本文将根据Oka et al.提出的变点估计修正单分位数方法进行样本尾指数变点检测,利用Cusum检验思想,主要是针对多元时间序列尾指数变点检测[8]。采用单分位数方法对多元时间序列进行样本尾指数变点检测。文章主要从以下方面进行:首先,进行模型基本假设介绍、检验统计量的构造和统计量极限分布的证明;其次,变点存在性检验及临界值的模拟计算;然后,针对三个经典厚尾分布类型模拟数据进行模拟研究,最后,利用本文提出的方法对深圳市香蜜湖路市委党校南行路段车流量数据进行变点存在性研究分析。
1 模型理论介绍
1.1 模型基本假设
利用变点检测模型检测多元时间序列中样本尾指数的变化,我们假设所有随机变量都被定义在概率空间(Ω,P)中。假设样本观测值为{Zit,i=1,…,n,t=1,…,T}是一个非负随机变量序列,其i是指某个个体(如:年),t是指时间(如:天)。设m是将样本划分为m+1段的m个未知变点,及T1,…,Tm为对应未知变点。对于每个i,假设Zit~fj,对于t∈[Tj-1,Tj),j=1,…,m+1,其中T0=1,Tm+1=T+1,fj是其分布函数,使得fj在实际应用中不同于fj-1和fj+1。为了避免估计的序列样本量过少,进行变点检测时默认对原序列存在以下可能的划分:Λε={(T1,…,Tm):Tj-Tj-1≥εT,T1≥εT,Tm≤(1-ε)T},其中ε>0是个较小的常数。Kim et al.提出的基于累积和检测时间序列尾指数变化的模型,将其应用到多元时间序列尾指数变点检测中。尾指数是衡量样本尾部分布的肥胖程度的指标[9]。对于该变点检测问题,有如下假设:
H0∶{Zit}尾指数无变点 vsHa∶尾指数存在变点。
设τ是样本的一个高分位点,则构造如下检验统计量,定义
(1)
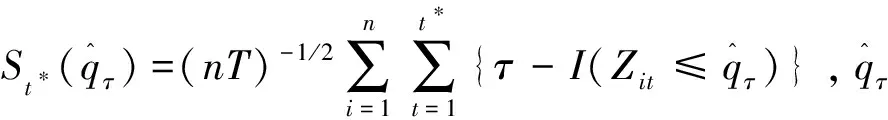
1.2 统计量渐近性质
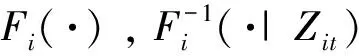
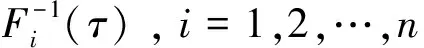
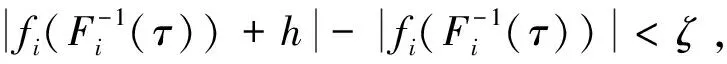
假设3
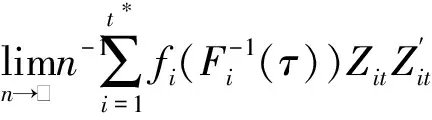
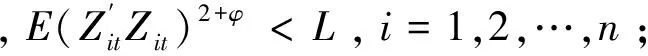
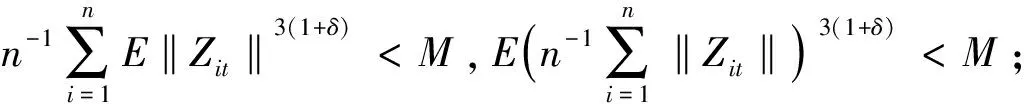
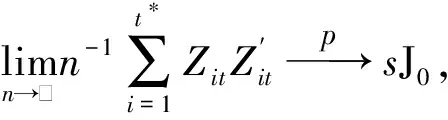
以上四个假设成立且在一定的正则条件下有:
(2)
其中s=t*/T。
根据式(1)和式(2)对该部分有:
=(τ(1-τ))1/2[W(s)-sW(1)]。
其中W(·)是一个维纳(WIENER)过程,则有
2 变点存在性检验
2.1 变点存在性检验步骤
对于变点问题,由变点检验统计量的极限分布得到变点检测法则,具体检测过程可分为三个步骤:
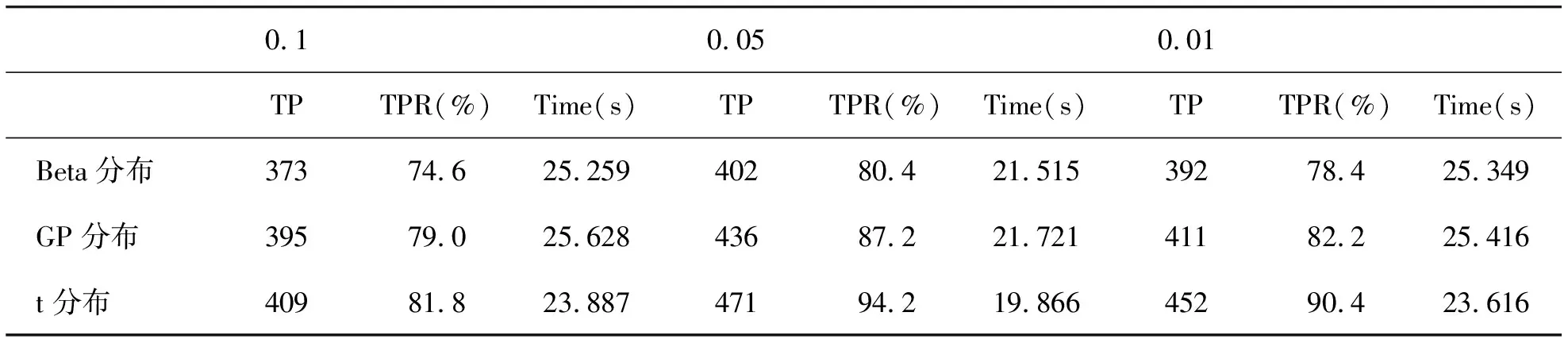
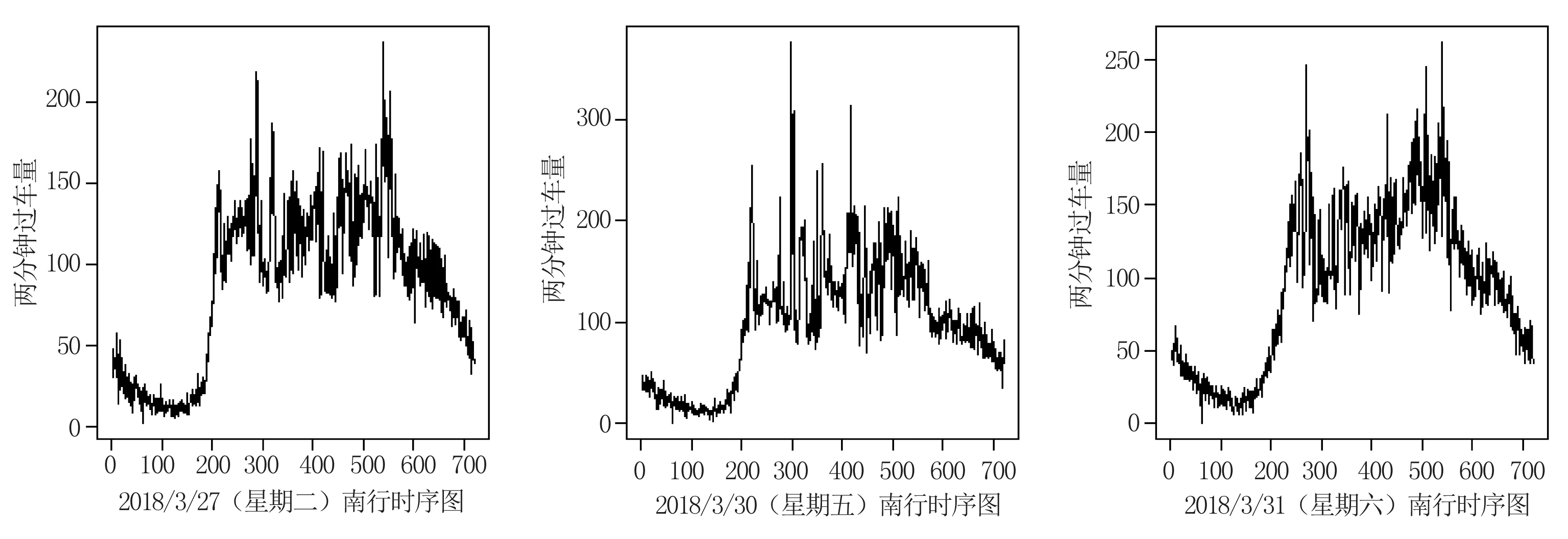
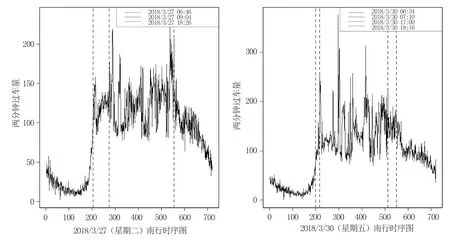
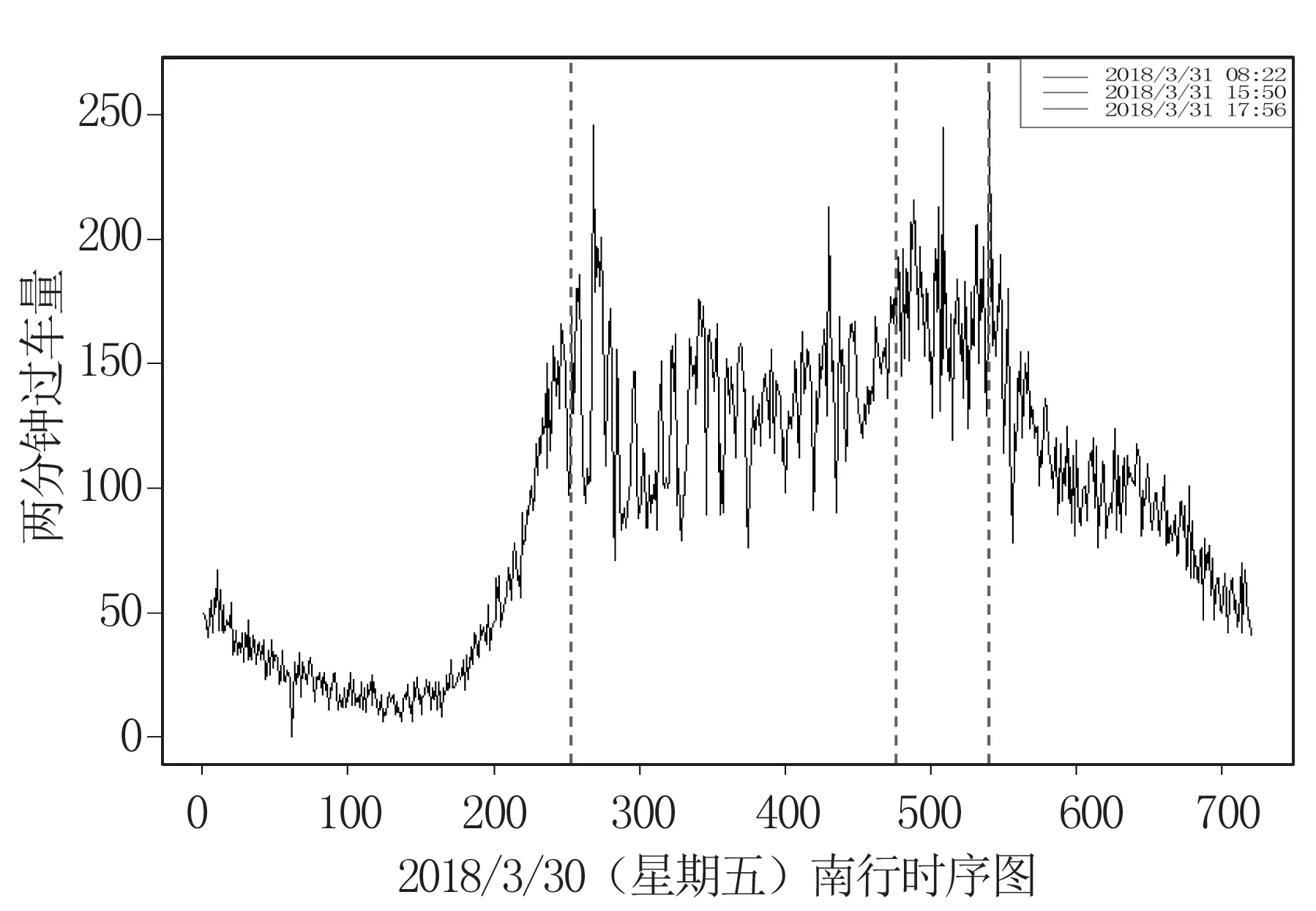
步骤1根据式子(1)可得到统计量SQτ,1的检验法则,如果SQτ,1 H0∶存在j个变点 vsHa∶存在j+1个变点。 步骤3重复步骤2,直到检测原假设失败或者当j=M时终止该检验程序,M是预先指定的变点个数的最大值。 利用数据模拟研究说明该方法的有效性。在模拟研究中,我们采用了分位数水平τ=0.95。为了不失一般性,考虑三个分布类型的数据,即Beta-,GP-和t-分布。总共产生了50年×365天的独立随机变量,设置变点位置为T1=182,在变点T1前数据的分布为f0,变点T1后数据的分布为f1,根据Dupuis D J.所定义数据的尾指数τ(F)理论计算公式如下[10], (3) 在不同分布下根据公式(3)得到尾指数τ(F)如表1所示。 表1 根据公式(3)计算得到样本尾指数 由尾指数计算公式得出的各样本尾指数情况如表1所示,可以看出在样本的参数变化时其尾指数也随之变化。 但在实际情况下,我们是无法从散乱的数据中观测到该变化。下面的模拟研究中我们将针对上述三个类型分布数据中检测其尾指数的变化,即尾指数变点存在性检验。 检验统计量的极限分布性质检测尾指数变点存在情况,由于临界值通过其极限分布不容易计算,所以通过蒙特卡洛模拟(Monte Carlo simulation)方式获得检验法则中的临界值,即在给定显著性水平为α的条件下,分别产生随机数εi,且εi~N(0,1)样本量为1000,模拟10000次,α分别取0.1,0.05,0.01,计算μn,1,得到10000次模拟最大值的(1-α)分位数即为对应α水平下的临界值,其结果展示如表2。 表2 给定显著性水平下的临界值 在得到给定显著性水平下的临界值之后,根据检验统计量对序列进行单变点检测,其实验模拟500次,其模拟结果如表3,其中TP表示真实变点数,TPR(%)表示500次模拟中检测出真实变点所占比例。 表3 模拟500次变点检测结果 由上表可以看出单分位数方法对多元时间序列尾指数变点检测在显著性水平α=0.05下准确度相对最高,且针对三个分布类型数据当分布从正态分布变化到t分布时检测正确率很高,说明该方法针对分布变化导致尾指数变化情形的变点识别更加精确,且运算速度较快,尤其对于t分布的检测时间比其他两种分布都少。 本实例分析数据源于深圳市局部区域道路的流量监测数据,主要选取深圳市香蜜湖路市委党校南行路段2018年3月27号(星期二)、2018年3月30号(星期五)和2018年3月31号(星期六)三天的数据为例,数据结构为每两分钟记录一次该路段车流量总数(一天共720个数据),根据实际数据得到过车量的时序图1所示。 图1 两分钟过车量时序图Fig.1 Two-minute traffic volumes sequence charts 分别以深圳市香蜜湖路市委党校南行路段2018年3月27号(星期二)、2018年3月30号(星期五)和2018年3月31号(星期六)三天的数据为例,利用本文的单分位数方法根据二分法原理将多变点转化为单变点问题进行变点检测,得到结果如图2、图3所示。 图2 2018.3.27(星期二)和2018.3.30(星期五)两天车流量变点检测结果Fig.2 Detection results of two-day change point of traffic flow on Tuesday and Friday, 2018.3.27 and 2018.30(Friday) 由图2(左)显示深圳市香蜜湖路市委党校南行路段2018年3月27号(星期二)车流量变点检测情况,检测结果显示存在三个变点,对应的位置分别是205、274、555,相对应的时间为 06∶46,09∶04、18∶26,2018年3月30号(星期五)车流量变点检测情况如图2(右)所示,检测结果显示存在四个变点,对应的位置分别是199、217、512、550且相对应的时间为 06∶34,07∶10、17∶00、18∶16,从检测结果容易看出工作日星期二和星期五有着类似的交通流变化规律,检测出早高峰7∶00~9∶00和晚高峰17∶00~19∶00都存在交通流变点,对于星期五而言变化情况更为复杂,这是因为星期五是一周中工作日的最后一天,人们都有各自的周末安排,在结束一周的工作后将出行旅游或者和朋友聚餐等活动,这就造成交通流变化规律有一定的变化,本文的检测结果和人们平时的出行规律相符合,证明了此方法的有效性。 2018年3月31号(星期六)车流量变点检测结果如图3所示。 从图3中2018年3月31号(星期六)车流量变点检测结果得到,在周末变点存在的时间为8∶22,15∶50,17∶56和上述工作日车流量变点检测结果相比,周末的早高峰要比工作日来得晚,而晚高峰变点存在情况和工作日相差不大,这是因为周末是人们在经过辛苦的一周工作后放松的时间,人们的生活习惯倾向于更加随意和散漫,人们都更愿意睡个舒服的懒觉再整理出门,这就导致了路段交通流变点的延迟,说明本文变点检测方法能有效地检测出交通流变点存在情况。 图3 2018.3.31(星期六)车流量变点检测结果Fig.3 2018.31(Saturday) traffic change point detection results 本文通过单分位数方法对多元时间序列尾指数变化进行变点检测。通过模拟研究证明了该方法的有效性,通过对交通数据的实例分析,得到该方法能准确检测到交通流中存在的变点,进而对于出行者而言了解该信息可以避免出行高峰期,提高出行效率,对于相关交管部门而言可根据该信息有效且快速地采取解决方案,一定程度上舒缓交通压力。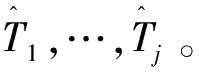
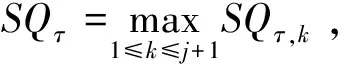
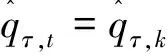
2.2 临界值的确定
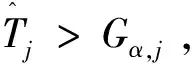
3 模拟研究
3.1 模拟数据介绍
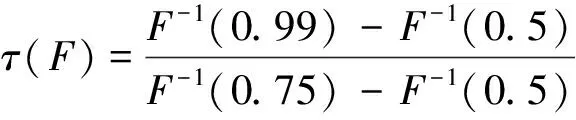
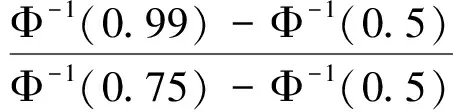

3.2 临界值的确定

3.3 变点检测

4 实例分析
5 总结

