最终严格对角占优矩阵的逆矩阵无穷范数的上界估计
李艳艳
(文山学院 数学学院, 云南 文山 663099)
数值分析中,矩阵A的逆矩阵A-1的‖A-1‖∞被用于计算条件数K(A)=‖A‖∞·‖A-1‖∞,所以对‖A-1‖∞的计算或估计,是矩阵理论研究的热点之一。近些年关于非奇异H矩阵类中的严格对角占优矩阵,弱链对角占优矩阵,Dashnic-Zusmanovich矩阵,Nekrasov矩阵,S-Nekrasov矩阵等的逆矩阵无穷范数的估计已得到了许多较好的结果[1-8]。而关于最终严格对角占优矩阵的研究,仅有文献[9,10]。 所以本文对最终严格对角占优矩阵的逆矩阵无穷范数的上界进行较为深入和详细的研究,在利用Nekrasov矩阵逆矩阵无穷范数已有估计式的基础上,得到了最终严格对角占优矩阵的‖A-1‖∞的一些新的改进的结果。
1 预备知识


设A=sI-B,其中s为复数,I为单位矩阵,B为复矩阵。如果存在正整数k使得skI-Bk为严格对角占优矩阵(SDD),就称A为最终严格对角占优矩阵(SDD∃),记作A∈SDD∃。
由文献[11]知,SDD⊆Nekrasov⊆H,SDD∃⊄H。
引理1(Varah界)[12]设矩阵A=(aij)∈Rn×n是严格对角占优矩阵,则



或

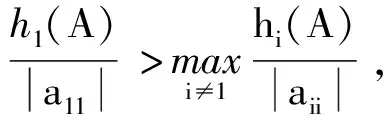
有



对于最终严格对角占优矩阵A的‖A-1‖∞的上界估计, 文献[9]和[10]都做了一定的研究。
引理5[9]如果存在正整数k使得A=sI-B∈SDD∃,则
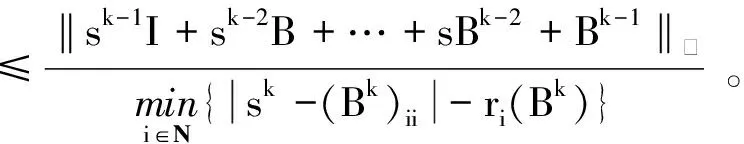
引理6[10]如果存在正整数k使得A=sI-B∈SDD∃,则

2 主要结果
本部分,利用引理2、引理3、引理4中的Nekrasov矩阵的逆矩阵无穷范数的估计式和SDD∃矩阵的定义式,给出SDD∃矩阵一些改进的新估计式。

‖A-1‖∞≤ ‖sk-1I+sk-2B+…+sBk-2+Bk-1‖∞×

则
(sI-B)-1=(skI-Bk)-1(sk-1I+sk-2B+…+
sBk-2+Bk-1),
即
‖A-1‖∞≤‖(skI-Bk)-1(sk-1I+sk-2B+…+sBk-2+Bk-1)‖∞
≤‖(skI-Bk)-1‖∞‖sk-1I+sk-2B+…+
sBk-2+Bk-1‖∞。
对skI-Bk应用引理2得,



‖A-1‖∞≤ ‖sk-1I+sk-2B+…+sBk-2+Bk-1‖∞
‖A-1‖∞≤‖sk-1I+sk-2B+…+sBk-2+Bk-1‖∞

‖sk-1I+sk-2B+…+sBk-2+Bk-1‖∞
< ‖sk-1I+sk-2B++sBk-2+Bk-1‖∞
定理3如果存在正整数k使得A=sI-B∈SDD∃,若
|sk-(Bk)11|-h1(skI-Bk)

有‖sk-1I+sk-2B+…+sBk-2+Bk-1‖∞

注:定理2和定理3说明,本文所给的估计式,从理论上提高了文献[9]和[10]中的结果。
下面用数值算例,对本文估计式的可行性和有效性,进一步说明。
3 数值算例

A1=5I-B1,取k=1,2,3,4,5,计算知k=2,3,4,5均是严格对角占优矩阵,所以A1∈SDD∃,应用本文定理2,3得‖A1-1‖∞≤0.8259, 事实上,‖A1-1‖∞=0.6667。
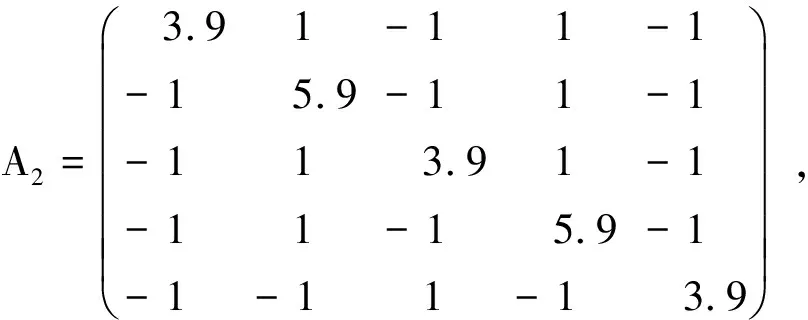
令A2=5I-B2,取k=1,2,3,4,5,计算知k=2,3,4,5均是严格对角占优矩阵,所以A1∈SDD∃,应用本文定理2,3得‖A2-1‖∞=0.5347, 事实上,‖A2-1‖∞=0.4657。

