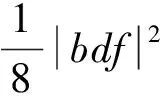基于概率信道的远程制备三比特态方案与实验研究

尹舟洋，王 旭,*，杨若傲

(1.贵州大学 大数据与信息工程学院，贵州 贵阳 550025; 2. 贵州省量子信息和大数据应用技术研究院，贵州 贵阳 550002)

1 基于概率信道的远程制备三比特态方案分析

实现基于概率信道的远程制备三比特态方案主要包括三个步骤[9]。

步骤一：三粒子非最大纠缠GHZ态量子信道的表达形式。在该方案中，需实现制备者在远处制备任意三量子比特纠缠态，假设量子态的制备者是Alice，而接收者为Bob，所需制备的量子纠缠态一般表示为

Ω=λ0|000〉+λ1eim1|001〉+λ2eim2|010〉+

λ3eim3|011〉+λ4eim4|100〉+λ5eim5|101〉+

λ6eim6|110〉+λ7eim7|111〉。

(1)

首先， Alice和Bob共享3对三粒子非最大纠缠GHZ态作为量子信道为

(2)

其中a,b,c,d,e,f都是复数，它们是信道系数，且都满足|b|≤|a|, |d|≤|c|, |f|≤|e|,以及a2+b2=1，c2+d2=1和e2+f2=1的归一化条件。粒子对(1,2,4,5,7,8)是属于Alice，粒子对(3,6,9)是属于Bob。然后，Alice利用1组由8个相互正交的矢量构成的测量基矢{ |φi〉}进行一个3粒子投影测量，其中粒子对(1,4,7)即为所测量的粒子，如果Alice的测量结果是|φ0〉，则粒子对(2,5,8,3,6,9)会坍缩成

ζ0′= (aceλ0|000000〉+acfλ1|001001〉+

adeλ2|010010〉+adfλ3|011011〉+

bceλ4|100100〉+bcfλ5|101101〉+

bdeλ6|110110〉+bdfλ7|111111〉)258369。

(3)

步骤二：进行本量子系统的系数信息测量。得到了粒子对(2,5,8,3,6,9)的坍缩态后，Alice将使用测量基测量粒子对(2,5,8)，且这8个测量基相互正交。然后，Alice利用测量基{ |ζi〉}，对它的粒子对(2,5,8)进行投影测量。经过了投影测量后，Alice将利用经典信道公布其测量结果，并以经典比特的方式传送给Bob。依据两者在远程制备前的约定和Alice发送的经典信息，Bob可确定粒子对(3,6,9)的坍缩态，能通过应用恰当的酉运算就能得到Ω的概率信息。另外，如果它的测量结果是|φ0〉和|φ0〉258，能得到粒子对(3,6,9)的坍缩态

adeλ2e-im2|010〉+adfλ3e-im3|011〉+

bceλ4e-im4|100〉+bcfλ5e-im5|101〉+

bdeλ6e-im6|110〉+bdfλ7e-im7|111〉)369。

(4)

步骤三：进行量子系统的相位测量。得到量子系统的系数信息后，为了得到想要制备的量子态，引入辅助粒子c，然后Bob对粒子对(3,6,9)进行酉变换，再测量辅助粒子c，当其结果为|0〉c，则量子对(3,6,9)即是想要制备的量子态

Ω=λ0|000〉+λ1eim1|001〉+

λ2eim2|010〉+λ3eim3|011〉+

λ4eim4|100〉+λ5eim5|101〉+

λ6eim6|110〉+λ7eim7|111〉。

(5)

2 基于IBM Q的单比特量子隐形传态实验

IBM量子实验平台是2016年IBM公司发布的一个基于超导量子态的5量子位通用量子计算机原型，它面向所有用户并可在云上访问。为了满足研究人员对基于量子处理器进行真实实验的需求，该平台提供了两种最常用的量子计算机原型，分别为IBM Q 5 Yorktown (5量子位)， IBM Q 5 Tenerife (5量子位)。在实验中，我们运用Hadamard门，X、Y、Z门(泡利矩阵)，旋转门S,S†,T,T†, Controlled-NOT (C-NOT)等门集来实现酉变换[10]。由于芯片布局不同，导致C-NOT中的控制量子位与目标量子位的选择需要考虑特殊的量子位实现，从而需要根据量子线路图的设计选择不同的芯片。针对该问题，IBM 量子实验平台做出了相对应的改进，使得用户可以自定义拓扑结构，十分有利于实验的便捷操作，本实验即是基于自定义拓扑结构进行研究。

通信双方是Alice和Bob，在两者分开之前，两者产生了一个EPR对，分开时每人带走EPR中的一个量子比特，分开后Alice需要向Bob发送一个量子比特|ψ〉，并与在Alice处的部分EPR对信息作用，然后测量此处的两个量子比特，得到可能的结果中的一个，并将信息发送给Bob，从而Bob根据Alice的信息，对他所拥有的EPR对信息进行操作，最后恢复原始的|ψ〉。

图1 单比特隐形传输线路图Fig.1 Single-qubit teleportation line diagram

量子保真度是指，用来度量两量子态间的距离的测度[12]。定义量子态ρ和σ间的保真度为

(6)

当量子保真度值接近于1时，两量子态ρ和σ间距离最近[12]。已知Alice发送的|0〉的概率信息为0.33，发送|1〉的概率信息为0.67，通过量子隐形传态，Bob接收的|0〉的概率信息为0.403，|1〉的概率信息为0.597，通过式(6)计算得到系统保真度为0.819。由此可知，该三比特量子远程态制备系统的通信效果较好，但是依然存在着其他因素影响量子远程态制备的质量，比如量子通信系统中量子门的误差，量子与量子门之间产生的误差，以及信道中的噪声。

3 基于振幅阻尼信道的远程制备单比特方案的研究

量子噪声，是使量子比特的本征态与量子系统所产生的非理想性交互作用的所有因素[12]。基于开放量子系统的研究，当噪声影响到信道时，会形成量子噪声信道模型，而振幅阻尼噪声会对信道振幅产生影响，它依据噪声算子的形式确定噪声系数值，从而改变了信道原有振幅。

3.1 基于振幅阻尼信道的远程制备单比特方案分析

基于振幅阻尼信道的远程制备单比特方案主要包括三个步骤[13]。

步骤一：加入振幅阻尼噪声的单比特量子信道的表示。在该方案中，有一个制备者Alice和接收者Bob，制备一个1量子比特态，它的形式为

φ=a0eim0|0〉+a1eim1|1〉。

(7)

|111〉〈000|+|111〉〈111|)。

(8)

已知振幅阻尼噪声算子[13]为

E0+=E0,

(9)

其中λ为噪声系数。该方案中加入振幅阻尼噪声算子，得到单比特振幅阻尼信道[14]。

步骤二：系数信息的测量。当得到了单比特振幅阻尼信道的表达式后，将测量该量子系统的系数信息。粒子A包含其系数，测量粒子A，表达式为

ρQM=|P0〉〈P0|βsource|P0〉〈P0|。

(10)

其中|P0〉=a0|0〉+a1|1〉。

步骤三：相位信息的测量。当测量得到了该量子系统的系数信息后，将进行其相位信息的测量。粒子B包含其相位信息，测量粒子B，表达式如下

(11)

a0a1(1-λ)eim0-im1|0〉〈1|+

a0a1(1-λ)eim1-im0|1〉〈0|+

(12)

步骤四：计算量子系统的保真度。为了检测该量子系统的偏移度，将计算其保真度

(13)

3.2 量子系统的保真度仿真与分析

(14)

分别绘出λ取0、0.25、0.5、0.75、1时的保真度曲线，如图2所示。

(a)量子系统保真度的二维曲线图 (b) 量子系统保真度的三维网格图图量子系统保真度仿真图 Quantum system fidelity simulation diagram

4 结语