UDD在消除制备簇态时次近邻相互作用中的应用

张纪英，陈佳君，吴 山，鲁望婷，陈红梅，赖重远

（江汉大学交叉学科研究院，湖北 武汉 430056）

簇态是一种特殊的量子纠缠态。在簇态基础上，仅仅通过适当的单量子比特测量就可以完成量子计算，而无需复杂的两量子比特门操作。鉴于簇态的这种重要性，很多研究人员致力于有关簇态的研究，其中一个关注的焦点就是簇态的制备［1-4］。

自旋模型是一种制备簇态的重要模型，现有很多簇态制备方案都是在自旋模型中提出的［5-6］。自旋模型中制备簇态的方案有些只考虑了自旋间相互作用比较强的最近邻相互作用［6］，有些考虑了最近邻和次近邻相互作用同时存在的情况［7］。文献［7］在制备簇态时，考虑的次近邻相互作用相当于一个噪声，会降低制备簇态的保真度。此文提出周期性动力学退耦合（periodic dynamic decoupling，PDD）能够有效抑制次近邻相互作用噪声，进而制备到高保真度的簇态。通常情况下，Uhrig动力学退耦合（Uh⁃rig dynamical decoupling，UDD）［8-10］对于噪声的抑制效果要优于PDD，即达到相同的噪声抑制效果时，UDD需要的脉冲总数要少。本文应用UDD来消除簇态制备过程中的次近邻相互作用噪声，并比较UDD和PDD两者对次近邻相互作用噪声的抑制效果。

1 研究系统的哈密顿量

考虑一个一维的含N个1/2自旋的自旋链，且量子比特之间是XY型的相互作用。此系统的哈密顿量为

其中J1是相互作用强度，可开关。分别是第i个量子比特的泡利X和Y算符。

应用此相互作用，通过第一步制备两量子比特的簇态对；第二步连接两量子比特簇态对形成一维簇态链，可以制备到理想的簇态用于量子计算［6］。在此相互作用基础上，综合考虑实际情况，文献［7］研究了存在次近邻相互作用时的系统。次近邻相互作用哈密顿量可以写为

其中J2是次近邻相互作用强度，其开关状态和J1同步。系统的总哈密顿量为

此时，由于次近邻相互作用H2的存在，应用文献［6］中的方案制备簇态时，实际得到的簇态距离理想簇态会有所偏离。此偏离的大小依赖于次近邻和最近邻相互作用强度之比，假设J2/J1=0.1。另外，偏离的大小可以用保真度F这个物理量来度量，F定义为

F的取值范围从0到1，其值越大，代表实际得到的簇态与理想簇态越接近，故F取值为1时最好，代表实际制备到的簇态与理想簇态完全重合。

2 应用PDD抑制次近邻相互作用的方案

文献［7］给出应用PDD抑制次近邻相互作用的方案。为了能够更好地描述本文的工作，笔者先简单介绍文献［7］中的结果。为了描述方便，以粒子数为4n（n为任意正整数）的自旋链为例。首先，在第一步制备两量子比特簇态对时，在第（4L-1）和第4L个量子比特上施加理想的沿Z方向的PDD脉冲序列，L=1，2，…，n。其次，在第二步连接第一步制备到的簇态对形成一维簇态链时，在第（4L-2）和第（4L-1）个量子比特上外加沿Z方向的PDD脉冲序列。经过上述两步PDD操作，次近邻相互作用可以被有效抑制，进而提高簇态的保真度。

以粒子数为4的自旋链为例分析上述两步PDD抑制次近邻相互作用的操作。图1为自旋数为4的自旋链，图中黑色实心圆点代表自旋，黑色实线代表最近邻相互作用，黑色点线代表次近邻相互作用。

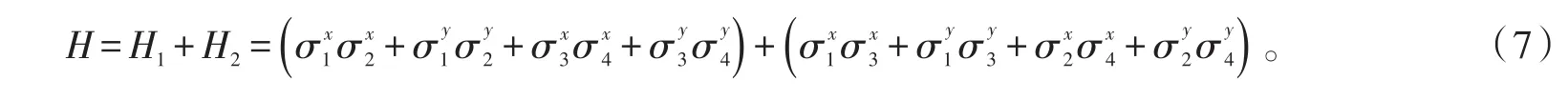
图1 自旋数为4的自旋链Fig.1 Spin chain with spin number as four

在第3和第4个自旋上外加沿Z方向的π脉冲，记此外加脉冲操作为UZ，此时系统的幺正演化算符为

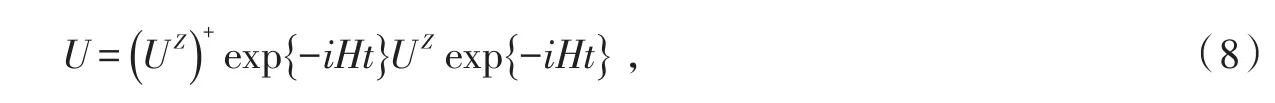
当t→0时，因为（8）式可以简化为

其中有效哈密顿量为

当第3和第4个量子自旋上外加沿Z方向的π脉冲时，UZ的具体表达形式为

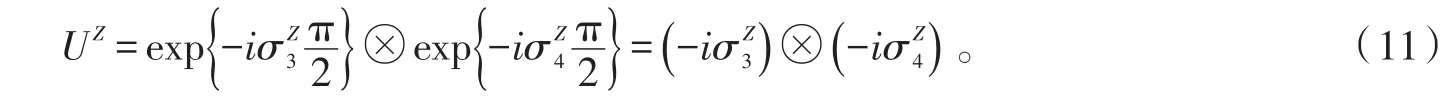
将（7）式和（11）式代入（10）式，可得

同理，可以得到第二步连接簇态对为簇态链时，在第2和第3个自旋上加沿Z方向的π脉冲后的有效哈密顿量为

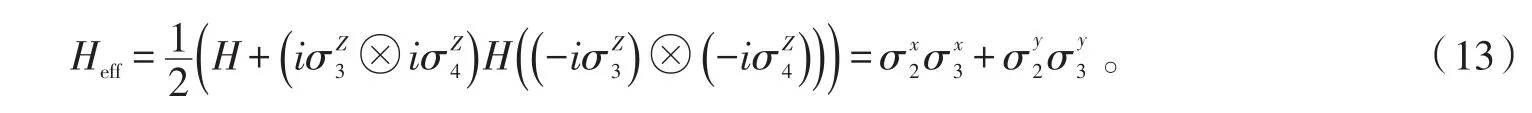
图2为文献［7］给出的数值模拟结果。由图2可知，没有外加PDD脉冲时，在粒子数为3的系统中，制备到的簇态的保真度数值要比1小较多，随着粒子数越来越多，制备到的簇态的保真度越来越小。当粒子数为10时，保真度已经小于0.8；当粒子数为12时，保真度已经小于0.75。对应这样小的保真度数值的簇态，已经不能很好地用于量子计算。当外加PDD脉冲数为2时，相较于没有外加PDD脉冲的情况，簇态保真度得到了很大的提高，粒子数从3到12，保真度始终远大于0.95，能很好地用于量子计算。当外加脉冲数由2增加到4时，保真度又得到了进一步增大，即随着外加脉冲数越多，制备到簇态的保真度越高。

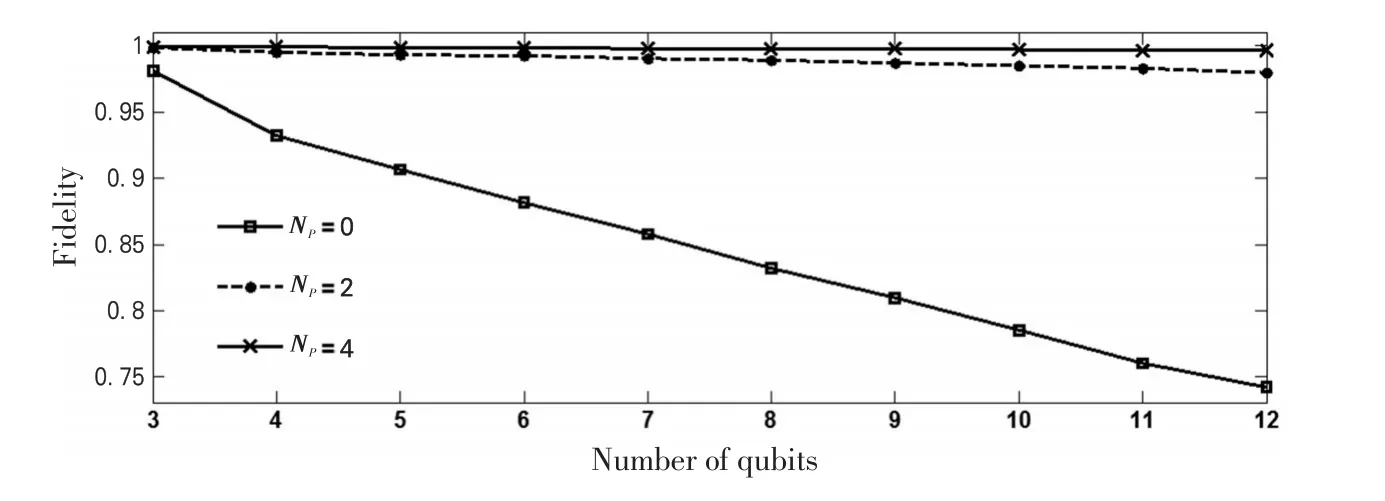
图2 应用PDD抑制次近邻相互作用噪声时制备到的簇态保真度Fig.2 Fidelity of generated cluster states when applied PDD for suppressing noise of next-nearest-neighbor interactions

3 应用UDD抑制次近邻相互作用的方案

UDD是继PDD之后在2007年由Uhrig通过最优化思想提出的一种在时间上非等间距的脉冲序列。通常情况下，达到相同的噪声抑制效果时，UDD的脉冲数要小于等间距的PDD的脉冲数。UDD施加第j个脉冲的时刻为δjt，

其中m为总脉冲数。

应用UDD抑制XY模型中的次近邻相互作用的操作，与文献［7］中应用PDD的操作相同，除了外加脉冲的施加时刻由改为（即首先在第（4L-1）和第4L个量子比特上施加理想的沿Z方向的UDD脉冲序列；其次在第（4L-2）和第（4L-1）个量子比特上外加沿Z方向的UDD脉冲序列）。图3和图4分别对应外加脉冲数为2和4时的脉冲序列示意图，T为制备簇态的总时间，黑色和白色矩形代表外加脉冲。其他脉冲数的示意图同样可以根据此处的外加脉冲时刻公式得到。由图3（a）和图4（a）可知，UDD脉冲序列中外加脉冲间的时间间距是非等间距的；由图3（b）和图4（b）可知，PDD中的脉冲间的时间间距是相等的。

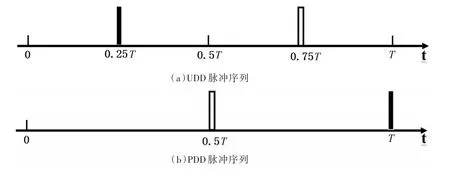
图3 外加脉冲数为2时的脉冲序列示意图Fig.3 Illustration of pulse sequences with applied pulse number as two

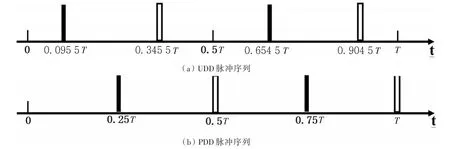
图4 外加脉冲数为4时的脉冲序列示意图Fig.4 Illustration of pulse sequences with applied pulse number as four

外加UDD脉冲序列后，通过计算对应的保真度来度量UDD对次近邻相互作用噪声的抑制效果。因为计算量过大，本文同文献［7］一样采用数值模拟方法计算保真度。因这里多为矩阵运算，笔者使用MATLAB软件进行数值计算。通过MATLAB程序，首先得到理想簇态，然后得到在有次近邻相互作用且有外加UDD脉冲序列时的实际态最后依照（6）式得到保真度。外加脉冲序列为PDD时保真度的数值计算方法同UDD时的情况。具体的数值模拟结果见图5。

由图5可知，当外加脉冲为2时，外加UDD脉冲序列对应的保真度要比PDD情况下的保真度高，更接近于1；当外加脉冲数增为4时，外加UDD脉冲序列依然要比PDD得到的保真度高，即脉冲数为2和4两种情况下，外加UDD脉冲序列时的保真度都要大于PDD时的保真度。可见在本文的模型中，UDD对次近邻相互作用噪声的抑制效果要优于PDD。从图5中还可以看到，外加脉冲数为4时的保真度要大于外加脉冲数为2时的保真度，可见外加脉冲数越多，UDD对次近邻的相互作用抑制效果越强。

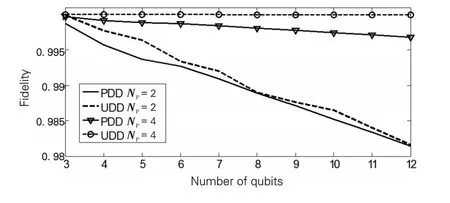
图5 应用UDD抑制次近邻相互作用噪声时制备到簇态的保真度Fig.5 Fidelity of generated cluster states when applied UDD for suppressing noise of next-nearest-neighbor interactions

4 结语

本文提出了在XY模型中制备簇态时，应用UDD抑制次近邻相互作用的方案，并与笔者之前发表的PDD方案做了对比。研究结果表明，当外加脉冲总数相同时，UDD方案中得到的簇态的保真度始终大于PDD方案中簇态的保真度。对于含12个粒子的自旋链系统，当外加脉冲数为4时，UDD方案能得到保真度为1的簇态，而PDD方案得到的簇态保真度要小于1，其需要多于4个脉冲才能制备到保真度为1的簇态。UDD方案提供了较好的抑制次近邻相互作用、制备高保真度簇态的方法，对基于簇态的量子计算及其相关的实验提供了较好的理论支持。

（References）

［1］HE G Q，SUN Y，HU L X，et al.Five-partite entanglement generation between two optical frequency combs in a quasi-peri⁃odicχ(2)nonlinear optical crystal［J］.Scientific Reports，2017，7（1）：1-8.

［2］YANG Z P，LI Z，MA S L，et al.One-step generation of continuous-variable quadripartite cluster states in a circuit QED sys⁃tem［J］.Physical Review A，2017，96（1）：012327.

［3］SCHWARTZ I，COGAN D，SCHMIDGALL E R，et al.Deterministic generation of a cluster state of entangled photons［J］.Science，2016，354（6311）：434-437.

［4］ZHANG C，HUANG Y F，LIU B H，et al.Experimental generation of a high-fidelity four-photon linear cluster state［J］.Physical Review A，2016，93（6）：062329.

［5］RAUSSENDORF R，WANG D S，PRAKASH A，et al.Symmetry-protected topological phases with uniform computational power in one dimension［J］.Physical Review A，2017，96（1）：012302.

［6］TANAMOTO T，LIU Y X，HU X，et al.Efficient quantum circuits for one-way quantum computing［J］.Physical Review Let⁃ter，2009，102（10）：100501.

［7］ZHANG J Y，ZHOU Z W，GUO G C.Eliminating next-nearest-neighbor interactions in the preparation of cluster state［J］.Chinese Physics Letters，2011，28（5）：050301.

［8］SINGH H，ARVIND，DORAI K.Experimental protection of arbitrary states in a two-qubit subspace by nested Uhrig dynami⁃cal decoupling［J］.Physical Review A，2017，95（5）：052337.

［9］CHAKRABORTY I，CHAKRABARTI A，RANGEET B.Enhancement of the accuracy of determination of transverse relax⁃ation time in solution state NMR spectroscopy by using Uhrig′s dynamic decoupling sequences［J］.Physical Chemistry Chemi⁃cal Physics，2015，17（48）：32384-32389.

［10］TEIXEIRA W S，KAPALE K T，PATERNOSTRO M，et al.Performance of dynamical decoupling in bosonic environments and under pulse-timing fluctuations［J］.Physical Review A，2016，94（6）：062322.