基于脉冲序列核的脉冲神经元监督学习算法

蔺想红,王向文,党小超

(西北师范大学计算机科学与工程学院,甘肃兰州 730070)

基于脉冲序列核的脉冲神经元监督学习算法

蔺想红,王向文,党小超

(西北师范大学计算机科学与工程学院,甘肃兰州 730070)

脉冲神经元应用脉冲时间编码神经信息,监督学习的目标是对于给定的突触输入产生任意的期望脉冲序列.但由于神经元脉冲发放过程的不连续性,构建高效的脉冲神经元监督学习算法非常困难,同时也是该研究领域的重要问题.基于脉冲序列的核函数定义,提出了一种新的脉冲神经元监督学习算法,特点是应用脉冲序列核构造多脉冲误差函数和对应的突触学习规则,并通过神经元的实际脉冲发放频率自适应地调整学习率.将该算法用于脉冲序列的学习任务,期望脉冲序列采用Poisson过程或线性方法编码,并分析了不同的核函数对算法学习性能的影响.实验结果表明该算法具有较高的学习精度和良好的适应能力,在处理复杂的时空脉冲模式学习问题时十分有效.

脉冲神经元;监督学习;脉冲序列核;内积;脉冲序列学习

1 引言

神经科学的研究成果表明,神经信息被编码为精确定时的脉冲序列,不仅仅是简单的脉冲发放频率[1].脉冲神经网络由更具生物真实性的脉冲神经元模型为基本单元构成[2],应用精确定时的脉冲序列表示与处理信息,是新一代神经网络计算模型.脉冲神经网络与基于脉冲频率编码信息的传统人工神经网络相比,拥有更强大的计算能力,是进行复杂时空信息处理的有效工具[3].实际上,要将脉冲神经元构成的网络应用于实际问题,特别是复杂时空模式识别问题的求解,关键在于构建高效的监督学习算法.脉冲神经元监督学习的目标是对于给定的突触输入脉冲序列,通过学习规则对突触权值的调整,产生任意的期望脉冲序列[4].对于脉冲神经网络来说,神经元内部状态变量及误差函数不再满足连续可微的性质,传统人工神经网络的学习算法已不能直接使用,需要研究者进一步构建具有广泛适用性的脉冲神经网络监督学习算法.

脉冲神经元及其网络的监督学习是新兴技术,对于监督学习算法的研究越来越受到研究者的关注,近年来提出了较多的监督学习算法[5,6].借鉴传统人工神经网络的误差反向传播算法,Bohte等人[7]提出了适用于前馈脉冲神经网络的SpikeProp算法,该算法限制网络中所有层的神经元只能发放一个脉冲.McKennoch等人[8]在该算法的基础上,提出了收敛速度更快的RProp和QuickProp算法.对于SpikeProp算法更加重要的扩展工作是Multi-SpikeProp算法,这类算法对脉冲神经网络输入层和隐含层神经元的脉冲发放没有限制,但仍然限制输出层神经元只能发放一个脉冲[9,10].最近,Xu等人[11]进一步提出了基于梯度下降的多脉冲监督学习算法,对网络中所有层神经元的脉冲发放没有限制,实现了输出层多脉冲的时空模式学习.SpikeProp及其扩展算法是一种数学分析方法,在学习规则的推导过程中,要求神经元模型的状态变量必须有解析的表达式.文献[12，13]将脉冲神经元的监督学习转换为分类问题,分别应用感知器学习规则和支持向量机实现了脉冲序列时空模式的在线学习算法.考虑神经元的脉冲时间依赖可塑性(Spike Timing-Dependent Plasticity,STDP)机制,Legenstein等人[14]给出了脉冲神经元的监督Hebbian学习算法,通过注入外部输入电流使学习神经元发放特定的期望脉冲序列.Ponulak和Kasiński[15]将突触权值的调整表示为STDP和anti-STDP两个过程的结合,提出了一种可对脉冲序列的复杂时空模式进行学习的远程监督方法(Remote Supervised Method,ReSuMe),该算法具有学习规则的局部特性和最优解的稳定性,并且可适用于各种神经元模型.虽然ReSuMe仅适用于单神经元或单层神经网络的学习,但基于其良好的适用性,已被广泛地应用在各类时空模式分类和识别问题.文献[16]结合SpikeProp算法,进一步将ReSuMe扩展到适用于线性神经元模型的多层前馈网络.Wade等人[17]应用BCM(Bienenstock-Cooper-Munro)规则与STDP机制,提出了多层前馈脉冲神经网络的SWAT(Synaptic Weight Association Training)算法.此外,Mohemmed和Schliebs[18]基于Widrow-Hoff规则给出了SPAN(Spike Pattern Association Neuron)学习规则,将脉冲序列应用卷积计算转换为模拟信号,通过转化后的输入脉冲序列,神经元期望输出和实际输出脉冲序列的误差调整突触权值.Yu等人[19]受SPAN的启发,提出了PSD(Precise-Spike-Driven)监督学习算法,突触权值的调整根据期望与实际输出脉冲的误差来判断,正的误差将导致长时程增强,负的误差将导致长时程抑制.

本文通过脉冲序列核的表示形式,将离散的脉冲序列转换为连续函数的分析过程,并可解释为特定的神经生理信号,比如神经元的突触后电位或脉冲发放的密度函数.将脉冲序列集合映射到与核函数对应的再生核Hilbert空间[20,21],这样便实现了脉冲序列的统一表示,以及脉冲序列相似性度量的形式化定义.我们通过定义脉冲序列随时间变化的误差函数以及神经元输入脉冲序列和输出脉冲序列之间的关系,给出了基于脉冲序列核的脉冲神经元的监督学习算法,突触权值的学习规则表示为脉冲序列的内积形式,实现了脉冲序列复杂时空模式的学习.为了描述方便,我们将所提学习规则命名为STKLR(Spike Train Kernel Learning Rule).该学习算法的特点在于:(1)突触学习规则的推导过程仅依赖于精确定时的脉冲序列,与神经元状态变量的表达方式无关,因此可适用于不同的神经元模型.(2)在学习算法的迭代过程中,学习率根据神经元实际输出脉冲序列的频率自适应地调整.(3)对神经元输入输出的脉冲序列编码方式没有限制,可适用于Poisson过程或线性方法等不同的时间编码策略.

2 脉冲序列核的表示

核方法是解决非线性模式分类问题的一种有效途径,其核心思想是通过某种非线性映射将原始数据嵌入到合适的高维特征空间,找出并学习一组数据中的相互关系[22].设x1,x2为初始空间中的点(在这里可以是标量,也可以是向量),非线性函数φ实现输入空间X到特征空间F的映射,核函数可表示为如下的内积形式:

κ(x1,x2)=〈φ(x1),φ(x2)〉

(1)

其中,κ(x1,x2)为核函数.下面我们将核函数的定义应用于神经元发放的脉冲序列,并推导突触权值的学习规则.

脉冲序列s={tf∈Γ:f=1,…,N}表示脉冲神经元在时间区间Γ=[0,T]所发放脉冲时间的有序数列,脉冲序列可形式化的表示为:

(2)

其中,tf表示第f个脉冲发放时间,δ(x)表示Dirac delta函数,当x=0时,δ(x)=1,否则δ(x)=0.

在定义脉冲序列的核函数之前,先给出脉冲时间的核函数表示,因为脉冲时间的核将组合构成脉冲序列核的表示.对于两个脉冲对应的发放时间tm和tn,可定义脉冲时间的核函数形式:

κ(tm,tn)=〈δ(t-tm),δ(t-tn)〉,∀tm,tn∈Γ

(3)

对于核函数κ要求具有对称、平移不变和正定特性,一般取Laplacian或Gaussian等核函数.比如Gaussian核表示为κ(tm,tn)=exp(-|tm-tn|2/2σ2).

由于脉冲序列是离散时间的集合,为了方便分析和计算,可以选择特定的光滑函数h,应用卷积将脉冲序列唯一地转换为一个连续函数:

(4)

由于脉冲序列所对应时间区间的有限性和连续函数fs(t)的有界性,可以得到:

(5)

也就是说,函数fs(t)是L2(Γ)空间的一个元素.脉冲序列空间中的元素si∈S(Γ)对应的函数fsi(t)将构成一个Hilbert空间,表示为L2(fsi(t),t∈Γ),并且是L2(Γ)的一个子空间[20].

对于任意给定的两个脉冲序列si,sj∈S(Γ),可在L2(fsi(t),t∈Γ)空间上定义其对应函数fsi(t)和fsj(t)的内积如下表示:

F(si,sj)=〈fsi(t),fsj(t)〉L2(Γ)=∫Γfsi(t)fsj(t)dt

(6)

应用脉冲时间核表示,进一步将式(6)重写为脉冲时间对的累加形式:

(7)

其中,κ(tm,tn)=∫Γh(t-tm)h(t-tn)dt.因此,F(si,sj)计算的时间复杂度为O(NiNj),Ni和Nj分别表示脉冲序列si和sj对应的脉冲数.

3 脉冲神经元的监督学习算法

3.1 脉冲序列的转换关系

脉冲神经元输入输出表示为脉冲序列的形式,即脉冲序列编码神经信息或外部刺激信号.假设突触前神经元输入的脉冲序列为si(t)∈S(Γ),i=1,…,N,突触后神经元输出的脉冲序列为so(t)∈S(Γ),为简化计算,将应用式(4)转换后的多个输入脉冲序列和输出脉冲序列在时间t的关系表达为线性组合关系:

(8)

其中,权值wi表示突触前神经元i和突触后神经元之间的连接强度,N表示突触前输入神经元的数目.做这种简化的原因在于:(1)将脉冲序列表达为线性组合关系,可以构造相应的学习规则进行神经元突触权值的学习,Carnell和Richardson给出了初步的结果[23];(2)如果将fs(t)解释为脉冲序列随时间变化的密度函数,对于广义的线性神经元模型,突触后神经元脉冲序列的密度函数可以表达为突触前神经元脉冲序列密度函数的线性组合形式.

3.2 突触权值的学习规则

构建脉冲神经元监督学习算法的关键是定义脉冲序列的误差函数,以及突触权值的学习规则.脉冲神经元在时间t的误差可定义为实际输出脉冲序列so∈S(Γ)和期望脉冲序列sd∈S(Γ)对应函数fs(t)的差值平方:

(9)

因此,脉冲神经元在时间区间Γ总的误差为

E=∫ΓE(t)dt.

应用脉冲序列误差函数对于突触权值的梯度计算值,使用delta更新规则对所有的突触权值进行调整.从突触前神经元i到突触后神经元的突触权值wi计算如下:

Δwi=-η▽Ei

(10)

其中,η表示学习率,▽Ei表示脉冲序列误差函数E对于突触权值wi的梯度计算值,可表示为误差函数E(t)对权值wi的导数在时间区间的积分:

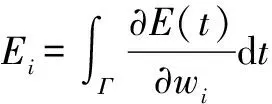
(11)

对于突触权值的学习规则,应用误差函数和链式规则,根据式(8)和式(9),突触权值wi在时间t的变化量可推导得到:

(12)

其中,si(t)∈S(Γ)表示输入神经元i所发放的脉冲序列.根据式(11),突触权值wi的调整值计算如下:

▽Ei=∫Γ[fso(t)-fsd(t)]fsi(t)dt=F(so,si)-F(sd,si)

(13)

根据以上所讨论的推导过程,我们给出了一个基于脉冲序列核的脉冲神经元监督学习新算法STKLR,突触学习规则表示如下:

Δwi=-η[F(so,si)-F(sd,si)]

(14)

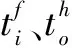
3.3 学习率的自适应方法

学习率的取值大小对学习过程的收敛速度有较大的影响,直接影响训练时间和训练精度.如果学习率取值太小,每次迭代中权值的有效更新值太小,将导致网络突触权值的收敛速度变慢;反之,容易使学习过程出现振荡,影响网络的收敛速度,甚至网络训练失败.根据神经元实际发放脉冲的频率自适应地调整学习率,可提高学习算法对突触权值训练的适应能力.

首先定义一个缩放因子c,使该算法的学习率η能够按照不同的脉冲发放频率自适应调整.假设神经元脉冲序列的发放频率为v,基准频率区间为[vmin,vmax],当v∈[vmin,vmax]时,缩放因子c=1,否则,c的表达式为:

(15)

学习率在基准频率区间的取值称为基准学习率η*,其值为给定频率区间的最佳学习率,具体分析过程在4.2节中给出.本文中基准频率区间的最小值vmin=40Hz,最大值vmax=60Hz.根据缩放因子c和频率区间内的基准学习率η*,学习率η的自适应调整方式为:

(16)

3.4 脉冲序列的相似性度量

在神经元的脉冲序列学习过程中,学习性能的评价就是判断在学习结束后实际发放的脉冲序列与期望输出脉冲序列接近的程度,这实际上就是度量两个脉冲序列之间的相似性.根据脉冲序列的内积所满足Cauchy-Schwarz不等式特性[20]:

F2(si,sj)≤F(si,si)F(sj,sj),∀si,sj∈S(Γ)

(17)

应用式(17)定义两个脉冲序列的相似性度量C,其表达式为:

(18)

4 实验结果

由于ReSuMe具有良好的学习能力和适用性,被广泛地应用在各类时空模式学习问题.因此,本文将所提STKLR与ReSuMe进行学习性能的比较.将ReSuMe突触权值随时间变化的调整量积分,可得突触权值的离线学习规则如下[19]:

(20)

其中,参数as=0.05表示non-Hebbian项,用于加速训练过程的收敛;指数形式的核函数定义了STDP机制所决定的Hebbian项,时间常量τs=5ms;No,Nd分别表示神经元实际输出脉冲序列so和期望脉冲序列sd的脉冲总数.

4.1 脉冲序列学习任务

4.1.1 脉冲序列的学习过程分析

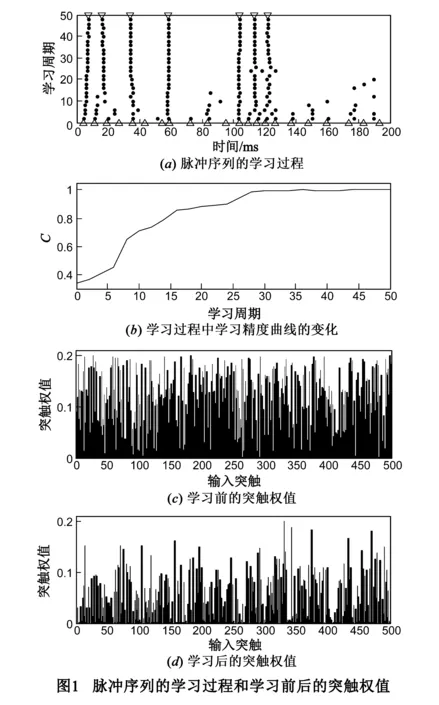
首先分析STKLR对于脉冲序列的学习过程和学习前后的突触权值变化情况,神经元学习的结果如图1所示.图1(a)展示了脉冲神经元的脉冲序列学习过程,图中▽表示期望输出脉冲序列,Δ表示脉冲神经元学习之前的输出脉冲序列,·表示学习过程中一些学习周期的实际输出脉冲序列.从学习过程可以看到,神经元经过大概45步就从初始的输出脉冲序列学习得到期望的输出脉冲序列.图1(b)表示学习过程中学习精度曲线的变化,可以看出在45个学习周期以后,实际输出和期望脉冲序列一样,即两者的相似度量值C达到1.图1(c)和图1(d)分别表示学习前和学习后的500个突触权值的变化情况.在学习过程中,神经元突触权值的变化范围为[0,0.2].通过脉冲序列学习过程的分析可以看出,STKLR可以对复杂的脉冲序列时空模式进行学习,并具有较好的学习能力.

4.1.2 参数变化时的学习性能分析

为了全面评价STKLR的学习性能,变化神经元的输入突触数目和脉冲序列的长度,并考察这些因素对学习性能的影响.第1组实验分析STKLR在输入突触数目逐渐增加时的学习性能.实验中神经元的输入突触数目从100到1000以间隔100逐渐增加,其它设定保持不变.图2(a)表示STKLR和ReSuMe在输入突触数目逐渐增加时的学习精度,从图中可以看出，随着神经元输入突触数目的逐渐增加,两个算法的学习精度都在增加,最终其度量C值可以非常接近1,且STKLR的学习精度高于ReSuMe的学习结果.例如,当输入突触数目为300时,STKLR的学习精度为0.9577,而ReSuMe的学习精度为0.9302;当输入突触数目为800时,STKLR的学习精度为0.9923,而ReSuMe的学习精度为0.9670.同时,学习精度在上升时期较大的标准方差显示此时STKLR学习性能的稳定性比较低,但是当学习精度达到很高的数值时,STKLR学习精度的标准方差则较小.图2(b)表示当学习精度达到最高时所需的学习周期,从图中可以看出,除过输入突触数目为200的情况外,STKLR所需的学习周期比ReSuMe的要少.例如,当输入突触数目为500时,STKLR所需的学习周期为522.81,而ReSuMe所需的学习周期为613.97;当输入突触数目为1000时,STKLR所需的学习周期为449.16,而ReSuMe的学习周期为702.74.

第2组实验分析STKLR在神经元输入与期望输出脉冲序列长度逐渐增加时的学习性能.实验中神经元输入与期望输出脉冲序列的长度从100ms到1000ms以间隔100ms逐渐增加,其它参数取基准值.图3所示为神经元输入与期望输出脉冲序列长度变化时的脉冲序列学习结果.图3(a)表示STKLR和ReSuMe在神经元输入与期望输出脉冲序列长度逐渐增加时的学习精度,从图中可以看出,随着脉冲序列长度的增加,两个算法的学习精度都在减小.此外,STKLR的学习精度高于ReSuMe学习精度,例如,当脉冲序列长度为200ms时,STKLR的学习精度为0.9933,而ReSuMe的学习精度为0.9785;当脉冲序列长度为1000ms时,STKLR的学习精度为0.7522,而ReSuMe的学习精度为0.6773.图3(b)表示随着神经元脉冲序列长度的增加,当学习精度达到最高时所需的最小学习周期.从图中可以看出,当脉冲序列长度为100ms、200ms、300ms、700ms、800ms、900ms和1000ms时,STKLR所需的学习周期少于ReSuMe.例如,当脉冲序列长度为300ms时,STKLR所需的学习周期为534.18,而ReSuMe所需的学习周期为587.94;当脉冲序列长度为1000ms时,STKLR所需的学习周期为432.61,而ReSuMe所需的学习周期为464.70.

4.1.3 期望脉冲序列不同编码的学习

为了进一步分析STKLR对脉冲序列的学习性能,输入脉冲序列采用Poisson过程生成,而期望脉冲序列分别采用Poisson过程和线性方法[17]两种不同的编码方式生成.实验中输入与期望输出脉冲序列的发放频率从20Hz到200Hz以间隔20Hz逐渐增加,并且输入脉冲序列与期望输出脉冲序列的发放频率相等,其它设定保持不变.图4所示为期望输出脉冲序列采用Poisson过程编码的学习结果.图4(a)表示STKLR和ReSuMe在输入与期望输出脉冲序列由不同发放频率的Poisson过程生成时的学习精度,随着脉冲序列发放频率的增加,两个算法的学习精度先减小后增大,且STKLR的学习精度高于ReSuMe.例如,当脉冲序列的发放频率为100Hz时,STKLR的学习精度为0.8860,而ReSuMe的学习精度为0.7906;当脉冲序列发放频率为200Hz时,STKLR的学习精度为0.8362,而ReSuMe的学习精度为0.7942.图4(b)表示当学习精度达到最高时算法所需的学习周期,从图中可以看出,STKLR算法所需的学习周期要少于ReSuMe,例如,当脉冲序列发放频率为200Hz时,STKLR所需的学习周期为449.15,而ReSuMe所需的学习周期为514.24.

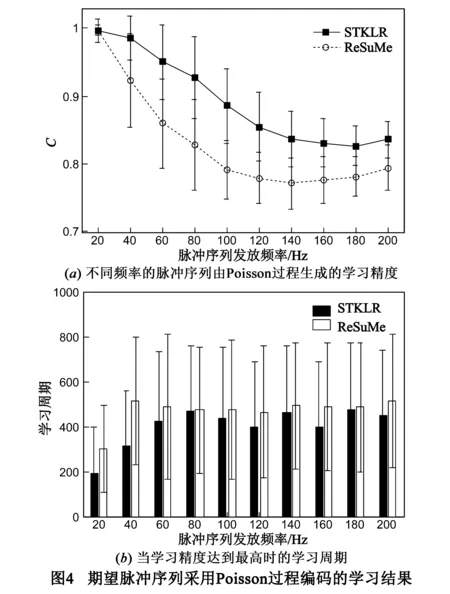
图5给出了期望输出脉冲序列采用线性方法编码的学习结果,这时脉冲序列中的相邻脉冲之间具有相同的时间间隔.从图5(a)中可以看出,随着脉冲序列发放频率的增加,STKLR的学习精度基本保持不变且接近于1,而ReSuMe的学习精度在逐渐减小之后又逐渐增大,并且ReSuMe的学习精度具有较大的标准方差,其学习稳定性比较差.图5(b)表示当学习精度达到最高时所需的学习周期,从图中可以看出,当脉冲序列的发放频率较小时,STKLR所需的学习周期少于ReSuMe,而当脉冲序列的发放频率大于120Hz时,STKLR所需的学习周期多于ReSuMe.

4.2 学习过程中学习率分析

4.2.1 基准学习率的确定

本组实验通过不同学习率的测试来确定在基准参数取值下适合STKLR和 ReSuMe的最佳学习率.实验中期望脉冲序列的发放频率为50Hz,学习率不采用式(16)调整,图6所示为学习率的取值分别为0.00005、0.0001、0.0005、0.001、0.005和0.01时的脉冲序列学习结果.图6(a)表示两个算法在学习率不同时的学习精度,从图中可以看出,随着学习率的增大,两个算法的学习精度都在增加.学习率为0.005时,STKLR的学习精度为0.9855,而ReSuMe的学习精度为0.9676.当学习率取0.01时两个算法的学习精度与学习率取0.005时的学习精度相比变化不大,但是学习精度的标准方差增大.当学习率进一步增大时将导致算法学习失败的次数增加.图6(b)表示两个算法在达到最高学习精度时所需的学习周期,从图中可以看出随着学习率的增大,两个算法所需的学习周期都在逐渐减少,且在学习率大于0.001时STKLR小于ReSuMe所需的学习周期.例如,当学习率为0.005时,STKLR所需学习周期的平均值为452.15,而ReSuMe的学习周期为631.21.因此,在我们的实验测试与分析中,学习率的取值0.005为两种算法的基准学习率.

4.2.2 学习率的变化过程

本组实验分析当期望输出脉冲序列由不同发放频率的Poisson过程或线性编码生成时,STKLR对脉冲序列学习中学习率的变化过程.实验中,输入脉冲序列由发放频率为20Hz的Poisson过程生成,期望输出脉冲序列的发放频率取20Hz、50Hz、100Hz和150Hz四个值,其它设定保持不变.图7表示期望输出脉冲序列的发放频率不同时学习率的变化过程,当学习周期大于200时学习率趋于稳定,因此图中只画出了前200个学习周期中的学习率.图7(a)所示为期望输出脉冲序列由不同发放频率的Poisson过程生成时学习率的变化过程,开始时神经元实际输出的脉冲较多,学习率从0.005迅速减小,之后随着学习周期的增加,学习率逐渐增大,最后趋于稳定.当期望输出脉冲序列的发放频率逐渐增大时,最终学习率逐渐减小.期望输出脉冲序列的发放频率分别取20Hz、50Hz、100Hz和150Hz时,对应的最终学习率分别为0.0101、0.0049、0.0022和0.0011.图7(b)所示为期望输出脉冲序列由线性方法编码时学习率的变化过程.从图中可以看出,学习率在学习过程中的变化情况与图7(a)相似.期望输出脉冲序列的发放频率分别取20Hz、50Hz、100Hz和150Hz时,对应的最终学习率分别为0.01、0.005、0.0017和0.0009.该实验说明本文提出的学习率自适应方法在学习过程中是有效的,能够在学习过程中根据神经元实际输出脉冲序列的发放频率对学习率进行自适应地调整.

4.3 核函数的比较与分析

4.3.1 不同核函数的表示

对于STKLR来说,突触权值的学习规则最终表示为脉冲序列核的累加形式,为了考察不同的核函数对STKLR学习性能的影响,我们选择Gaussian核函数、Laplacian核函数、α-核函数以及Inverse Multiquadratic核函数,使用这些核函数对算法进行测试.本文中采用的核函数如表1所示.

表1 脉冲序列的核函数

4.3.2 核函数的学习性能

由于本文前面的实验中STKLR均采用Gaussian核函数,首先在基准参数下对Gaussian核的参数σ进行分析.图8给出了Gaussian核函数在参数不同时的脉冲序列学习结果,Gaussian核的参数σ取值分别为0.1、0.5、1、2、5和10共六个值.图8(a)所示为核函数参数不同时的学习精度.从图中可以看出,随着核函数参数σ的增大,STKLR的学习精度在σ=0.1时为0.6025;随着σ的增大,学习精度逐渐增大,当σ=2时C达到最大值0.9933,但当σ进一步增大时,学习精度逐渐减小.图8(b)所示为学习精度达到最高时所需的学习周期,其变化过程表明所需学习周期先减少,然后逐渐增多.当σ=0.5时,所需学习周期为693.95;当σ=2时,所需学习周期为522.81.根据以上分析,核函数的参数对学习精度有较大的影响,我们在实验中,Gaussian核函数的最佳参数σ的值取为2.

图9表示核函数分别为Gaussian核(G),Laplacian核(L),α-核(A),Inverse Multiquadratic核(IM)时的脉冲序列学习结果,其中Gaussian核的参数为0.5,Laplacian核的参数为5,α-核的参数为0.5,Inverse Multiquadratic核的参数为1.图9(a)所示为核函数不同时的学习精度,图9(b)所示为当学习精度达到最高时所需的学习周期.此外,通过实验发现多项式核,Sigmoid核,Multiquadratic核等不适用于STKLR,使用这些核函数时将导致算法学习失败或学习效果太差,而Gaussian核,Laplacian核,α-核,Inverse Multiquadratic核等可以得到理想的学习效果,实现对复杂脉冲序列模式的学习.

从以上实验结果可以看出,应用监督学习算法STKLR对脉冲序列时空模式进行学习时,核函数类型和参数的选择非常重要.核函数的类型选择和参数优化方法主要有[25]:(1)对于选定的核函数,可采用遍历方式对一个区间内的核参数逐个进行测试和比较.首先为核函数的参数赋初始值,然后开始实验测试,根据测试精度重复调整核参数值,直至得到满意的测试精度为止.该方法简单可行,特别是对于本文中核函数参数只有一个的情况,容易得到合适的参数值.但缺点是凭经验调整,缺乏足够的理论依据,在参数调整过程中带有一定的盲目性；(2)使用目标函数自适应地选择最佳的核参数,目前较多应用遗传算法优化核函数类型以及参数.但是该类方法在每一次进化过程中,对于群体中的每一个参数,都要进行一次脉冲神经网络的监督学习迭代过程,增加了算法的时间和空间复杂性.

5 结论

脉冲神经元应用精确定时的脉冲序列编码信息,本文基于脉冲序列核函数的定义,提出了一种基于脉冲序列核的脉冲神经元监督学习算法STKLR,并在学习过程中通过脉冲序列的实际发放频率自适应地调整学习率，实现了对脉冲序列复杂时空模式的有效学习.通过脉冲序列学习过程的分析,以及不同输入突触数目、不同脉冲序列长度、不同输入与期望输出脉冲序列发放频率、不同核函数和核函数参数等因素对算法学习性能影响的分析,表明本文所提出的STKLR具有较好的脉冲序列学习能力,并且比ReSuMe具有较高的学习精度和较小的学习周期.此外,从STKLR的推导过程可以看出,其学习规则表现为以核函数表示的脉冲序列内积形式,与具体脉冲神经元状态变量的表达方式无关,可适用于不同神经元模型.脉冲序列的核函数及其内积理论目前主要用于脉冲序列的相似性度量,较少直接应用于脉冲神经网络监督学习算法的构造,STKLR可以看作是一种基于脉冲序列内积操作的脉冲神经网络监督学习算法的一般性框架.

进一步的工作考虑将STKLR应用到实际的时空模式分类和识别问题,如图像分类和语音识别等.应用脉冲神经网络的监督学习对具体问题的求解可分为三个步骤:首先,将样本数据(如数值、图像或语音数据)的每个分量应用特定的编码策略编码为精确定时的脉冲序列,并对样本所属类别设定期望的脉冲序列;然后,将多个脉冲序列输入网络中的脉冲神经元,得到实际输出的脉冲序列;最后,根据实际输出脉冲序列和期望脉冲序列的误差,应用STKLR算法的学习规则对神经网络的突触权值进行调整.通过算法的多次迭代过程,当误差小于设定的最小值或达到最大学习周期时,学习过程结束,并用得到的脉冲神经网络进行模式分类或识别.

[1]Quiroga R Q,Panzeri S.Principles of Neural Coding[M].Boca Raton,FL:CRC Press,2013.

[2]蔺想红,张田文.分段线性脉冲神经元模型的动力学特性分析[J].电子学报,2009,37(6):1270-1276. Lin Xiang-hong,Zhang Tian-wen.Dynamical properties of piecewise linear spiking neuron model[J].Acta Electronica Sinica,2009,37(6):1270-1276.(in Chinese)

[3]Ghosh-Dastidar S,Adeli H.Spiking neural networks[J].International Journal of Neural Systems,2009,19(4):295-308.

[4]Memmesheimer R M,Rubin R,Ölveczky B P,et al.Learning precisely timed spikes[J].Neuron,2014,82(4):925-938.

[5]Kasiński A,Ponulak F.Comparison of supervised learning methods for spike time coding in spiking neural networks[J].International Journal of Applied Mathematics and Computer Science,2006,16(1):101-113.

[6]蔺想红,王向文,张宁,等.脉冲神经网络的监督学习算法研究综述[J].电子学报,2015,43(3):577-586. Lin Xiang-hong,Wang Xiang-wen,Zhang Ning,et al.Supervised learning algorithms for spiking neural networks:A review[J].Acta Electronica Sinica,2015,43(3):577-586.(in Chinese)

[7]Bohte S M,Kok J N,La Poutré J A.Error-backpropagation in temporally encoded networks of spiking neurons[J].Neurocomputing,2002,48(1-4):17-37.

[8]McKennoch S,Liu D,Bushnell L G.Fast modifications of the SpikeProp algorithm[A].Proceedings of the International Joint Conference on Neural Networks[C].Vancouver,Canada:IEEE,2006.3970-3977.

[9]Booij O,Nguyen T H.A gradient descent rule for spiking neurons emitting multiple spikes[J].Information Processing Letters,2005,95(6):552-558.

[10]Ghosh-Dastidar S,Adeli H.A new supervised learning algorithm for multiple spiking neural networks with application in epilepsy and seizure detection[J].Neural Networks,2009,22(10):1419-1431.

[11]Xu Y,Zeng X,Han L,et al.A supervised multi-spike learning algorithm based on gradient descent for spiking neural networks[J].Neural Networks,2013,43:99-113.

[12]Xu Y,Zeng X,Zhong S.A new supervised learning algorithm for spiking neurons[J].Neural Computation,2013,25(6):1472-1511.

[13]Le Mouel C,Harris K D,Yger P.Supervised learning with decision margins in pools of spiking neurons[J].Journal of Computational Neuroscience,2014,37(2):333-344.

[14]Legenstein R,Naeger C,Maass W.What can a neuron learn with spike-timing-dependent plasticity?[J].Neural Computation,2005,17(11):2337-2382.

[15]Ponulak F,Kasinski A.Supervised learning in spiking neural networks with ReSuMe:Sequence learning,classification,and spike shifting[J].Neural Computation,2010,22(2):467-510.

[16]Sporea I,Grüning A.Supervised learning in multilayer spiking neural networks[J].Neural Computation,2013,25(2):473-509.

[17]Wade J J,McDaid L J,Santos J A,et al.SWAT:A spiking neural network training algorithm for classification problems[J].IEEE Transactions on Neural Networks,2010,21(11):1817-1830.

[18]Mohemmed A,Schliebs S.SPAN:Spike pattern association neuron for learning spatio-temporal spike patterns[J].International Journal of Neural Systems,2012,22(4):786-803.

[19]Yu Q,Tang H,Tan K C,et al.Precise-spike-driven synaptic plasticity:Learning hetero-association of spatiotemporal spike patterns[J].PLoS One,2013,8(11):e78318.

[20]Paiva A R C,Park I,Príncipe J C.A reproducing kernel Hilbert space framework for spike train signal processing[J].Neural Computation,2009,21(2):424-449.

[21]Park I M,Seth S,Paiva A R C,et al.Kernel methods on spike train space for neuroscience:A tutorial[J].IEEE Signal Processing Magazine,2013,30(4):149-160.

[22]Xu J,He M,Han J,et al.A comprehensive estimation method for kernel function of radar signal classifier[J].Chinese Journal of Electronics,2015,24(1):218-222.

[23]Carnell A,Richardson D.Linear algebra for times series of spikes[A].Proceedings of the 13th European Symposium on Artificial Neural Networks[C].Evere,Belgium:d-side,2005.363-368.

[24]Gerstner W,Kistler W M.Spiking Neuron Models:Single Neurons,Populations,Plasticity[M].Cambridge:Cambridge University Press,2002.

[25]Zhao M,Ren J,Ji L,et al.Parameter selection of support vector machines and genetic algorithm based on change area search[J].Neural Computing and Applications,2012,21(1):1-8.

蔺想红 男,1976年1月生于甘肃天水.2009年获哈尔滨工业大学计算机应用技术专业博士学位,现任西北师范大学计算机科学与工程学院教授,硕士生导师.研究方向为神经网络、进化计算、人工生命、图像处理.

E-mail:linxh@nwnu.edu.cn

王向文 男,1991年3月生于甘肃天水.2015年获西北师范大学软件工程专业硕士学位.研究方向为神经网络、机器学习.

E-mail:wangxiangwen2@163.com

党小超(通信作者) 男,1963年9月生于甘肃兰州.1995年获西北工业大学计算机应用技术专业硕士学位,现任西北师范大学计算机科学与工程学院院长、教授,硕士生导师.研究方向为计算机网络、无线传感器网络、智能信息处理.

E-mail:dangxc@nwnu.edu.cn

A New Supervised Learning Algorithm for Spiking Neurons Based on Spike Train Kernels

LIN Xiang-hong,WANG Xiang-wen,DANG Xiao-chao

(SchoolofComputerScienceandEngineering,NorthwestNormalUniversity,Lanzhou,Gansu730070,China)

The purpose of supervised learning with temporal encoding for spiking neurons is to make the neurons emit arbitrary spike trains in response to given synaptic inputs.However,due to the discontinuity in the spike process,the formulation of efficient supervised learning algorithms for spiking neurons is difficult and remains an important problem in the research area.Based on the definition of kernel functions for spike trains,this paper proposes a new supervised learning algorithm for spiking neurons with temporal encoding.The learning rule for synapses is developed by constructing the multiple spikes error function using spike train kernels,and its learning rate is adaptively adjusted according to the actual firing rate of spiking neurons during learning.The proposed algorithm is successfully applied to various spike trains learning tasks,in which the desired spike trains are encoded by Poisson process or linear method.Furthermore,the effect of different kernels on the performance of the learning algorithm is also analyzed.The experiment results show that our proposed method has higher learning accuracy and flexibility than the existing learning methods,so it is effective for solving complex spatio-temporal spike pattern learning problems.

spiking neuron;supervised learning;spike train kernel;inner product;spike train learning

2015-04-07;

2015-07-01;责任编辑：梅志强

国家自然科学基金(No.61165002，No.61363059);甘肃省自然科学基金(No.1506RJZA127);甘肃省高等学校科研项目(No.2015A-013)

TP183

A

0372-2112 (2016)12-2877-10

��学报URL:http://www.ejournal.org.cn

10.3969/j.issn.0372-2112.2016.12.010