基于协作多点下行传输的非线性鲁棒预编码
顾浙骐,张忠培
(电子科技大学通信抗干扰技术国家级重点实验室,四川成都 611731)
基于协作多点下行传输的非线性鲁棒预编码
顾浙骐,张忠培
(电子科技大学通信抗干扰技术国家级重点实验室,四川成都 611731)
对于协作多点系统,下行信道信息误差会大幅降低联合传输的性能.为了避免下行信道信息误差对联合传输的影响,本文利用其二阶统计特性,设计了非线性鲁棒预编码算法.由于协作多点系统的特点和非线性鲁棒预编码的结构会导致用户间的性能差异,本文通过优化非线性鲁棒预编码算法的连续干扰消除先后顺序,从而改善性能最差用户的误码率,降低非线性鲁棒预编码算法的平均误码率.仿真结果表明当下行信道信息误差存在时,本文所提出的非线性鲁棒预编码性能优于传统的线性和非线性预编码性能.仿真结果还表明优化排序能提高非线性鲁棒预编码的性能增益.
无线通信;协作多点;非线性鲁棒预编码
1 引言
协作多点技术(Coordinated MultiPoint,CoMP)作为未来蜂窝网络备选技术,能消除同频小区之间的干扰,改善小区边缘用户吞吐量,大幅提高系统频谱资源效率[1~3].根据基站的协作方式,CoMP下行传输可分为协作波束成形(Coordinated Beamforming,CB)和联合传输(Joint Transmission,JT)[4,5].其中,联合传输是指各同频小区的基站通过有线链路连接到中央控制单元(Central Union,CU),与各小区用户构成一个虚拟多输入多输出系统(Virtual Multiple Input Multiple Output,Virtual MIMO),实现下行传输.联合传输通过预编码,可获得较现有无线通信系统1倍以上的性能增益[6].
由于预编码需要理想的下行信道信息(Channel Side Information,CSI),因此基站如何获得准确的下行CSI成为联合传输实现的关键.时分双工(Time Division Duplex,TDD)模式利用信道互易特性,使基站能通过上行导频估计获得下行CSI,从而避免了频分双工(Frequency Division Duplex,FDD)模式的反馈开销及量化误差[7].因此,TDD模式被认为更易于协作多点技术的实现.若非特殊说明,后文中的系统均采用TDD模式.尽管TDD模式的信道互易特性保证了在相干时间内上行CSI与下行CSI相等,但由于基站对上行CSI的估计存在误差,基站无法获得准确的上行CSI,则基站获得的下行CSI也存在误差.
文献[5]分析了下行CSI误差对联合传输可达速率的影响.其分析结果表明下行CSI误差导致预编码无法完全消除各用户间的干扰,使CoMP的可达速率大幅下降,造成系统性能损失.文献[8]推导了当下行CSI误差存在时,联合传输对应各用户的等效信干噪比(Signal to Interference Noise Ratio,SINR),通过对各用户的传输速率匹配和对各协作基站的发送功率分配,优化了最差条件下(worst case)系统的加权和速率(weighted sum rate).文献[9]针对TDD模式的联合传输,设计了迭代算法以获得最优的线性预编码矩阵和线性接收矩阵.该算法对下行CSI误差具有鲁棒性,但其迭代操作收敛慢,复杂度高.文献[8]以最小化均方误差(MMSE)为准则,设计了线性鲁棒预编码.与传统线性MMSE预编码相比,该预编码能在下行CSI存在误差时获得性能增益.
现阶段联合传输的鲁棒预编码通常基于线性预编码的结构进行设计和优化.然而线性预编码的性能与非线性预编码的性能仍存在较大差距[9].同时,现阶段联合传输的鲁棒预编码通常假设协作基站与不同用户之间的下行CSI误差为独立同分布.然而由于实际联合传输的拓扑特点,协作基站与不同用户之间的下行CSI误差通常具有不同的方差.基于以上两点,本文首先根据TH预编码(Tomlinson-Harashima precoding)的结构,设计了针对下行CSI误差的非线性鲁棒预编码.然后,本文通过优化该预编码连续干扰消除的先后顺序,从而改善性能最差用户的误码率,降低联合传输的平均误码率.最后,本文通过仿真验证了本文所提出算法的性能.仿真结果表明当协作传输存在下行CSI误差时,本文所设计非线性鲁棒预编码的性能优于传统的线性预编码和线性鲁棒预编码[8].同时,仿真结果还表明优化排序能帮助非线性鲁棒预编码获得更大的性能增益.

2 系统模型
采用联合传输模式的协作多点系统有Nb个协作基站,各基站均装配nt根天线,有M个用户,各用户均装配单根天线.各协作基站通过光纤连接到中央控制单元,通过联合传输模式实现对各用户的下行传输.各协作基站到用户m的上下行信道可表示为
Hm-UL=[hm1-UL…hmb-UL…]∈1×Nbnt
Hm-DL=[hm1-DL…hmb-DL…]∈1×Nbnt
(1)
其中hmb-UL,hmb-DL∈1×nt分别表示协作基站b与用户m间的上行与下行信道,为复数集.
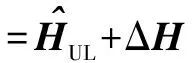
(2)
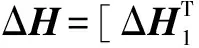
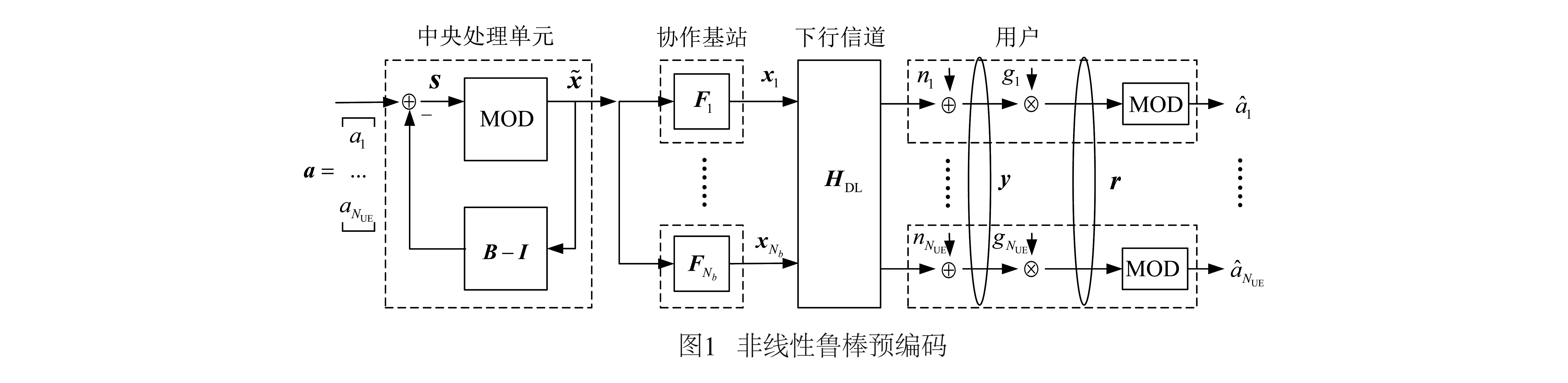
ΔH中各元素的大小与其对应用户的SRS到达基站的等效信噪比(Signal Noise Ratio,SNR)成反比[11],则假设ΔH中的元素为相互独立的零均值复正态分布随机变量,ΔH~CN(0,CΔH).其中CΔH为ΔH的自相关矩阵,如下所示:
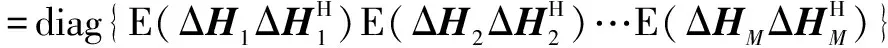
(3)
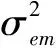
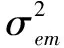
(4)
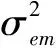
3 非线性鲁棒预编码
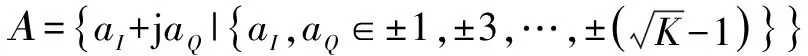
(5)
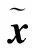
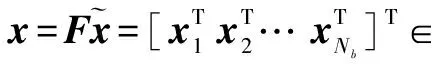
(6)
其中前馈矩阵F为酉阵.发射向量x经过下行信道HDL,并在各用户接收端叠加高斯白噪声nm,m=1,…,M,同时乘以各自所对应的缩放因子gm,m=1,…,M,得到接收信号矢量
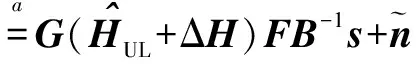
(7)
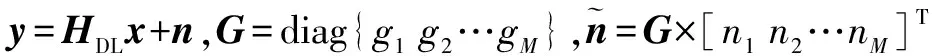
在此,我们通过对反馈矩阵B,前馈矩阵F以及对角缩放矩阵G的优化设计,实现非线性鲁棒预编码,降低下行误差对联合传输的影响.定义接收误差矢量e
e=r-s
(8)
通过求解下述最小化问题,确定反馈矩阵B,前馈矩阵F以及对角缩放矩阵G
(9)
式(9)的本质为最小化接收信号矢量r与等效信号矢量s的均方误差(Mean Square Error,MSE).根据最小均方误差(Minimum Mean Square Error,MMSE)最优解的正交原理(或者叫投影定理)[12],则接收误差矢量e与矢量y满足
(10)
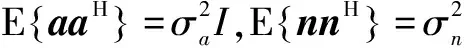
(11)
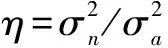
(12)
由于前馈矩阵F为酉阵,由酉阵的性质FHF=I,我们可以得到
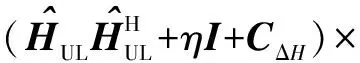
(13)
η和CΔH已知,同时式(13)的等式右边部分为正定Hermite矩阵,通过对式(13)的等式右边部分作乔里斯基分解(Cholesky Factorization),我们则可得到下三角矩阵L=G-1B.同时,通过下三角矩阵L,我们可以得到满足式(9)的反馈矩阵B,前馈矩阵F以及对角缩放矩阵G的表达式
G=diag{L(1,1)-1L(2,2)-1…L(M,M)-1}
B=GL
(14)
为了便于后续的优化排序,我们将上述的非线性鲁棒预编码改写为等价形式,在此定义
(15)
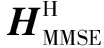
(16)
根据式(16),式(14)中反馈矩阵B,前馈矩阵F以及对角缩放矩阵G可重新表示为
G=diag{R(1,1)-1R(2,2)-1…R(M,M)-1}
B=GRH
F=Q
(17)
式(17)中的反馈矩阵B,前馈矩阵F以及对角缩放矩阵G和式(14)中的等价.
4 非线性鲁棒预编码的优化排序
根据式(17)的反馈矩阵B,前馈矩阵F以及对角缩放矩阵G,我们得到误差矢量e的协方差矩阵
Ce=E{eeH}=GΣG
(18)
其中
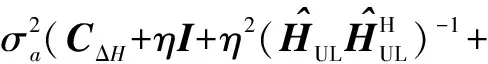
(19)
由式(18)和式(19),我们可以发现各用户接收误差的方差为
[E{|e1|2}E{|e2|2}…E{|eM|2}]= [Ce(1,1)Ce(2,2)…Ce(M,M)]
(20)
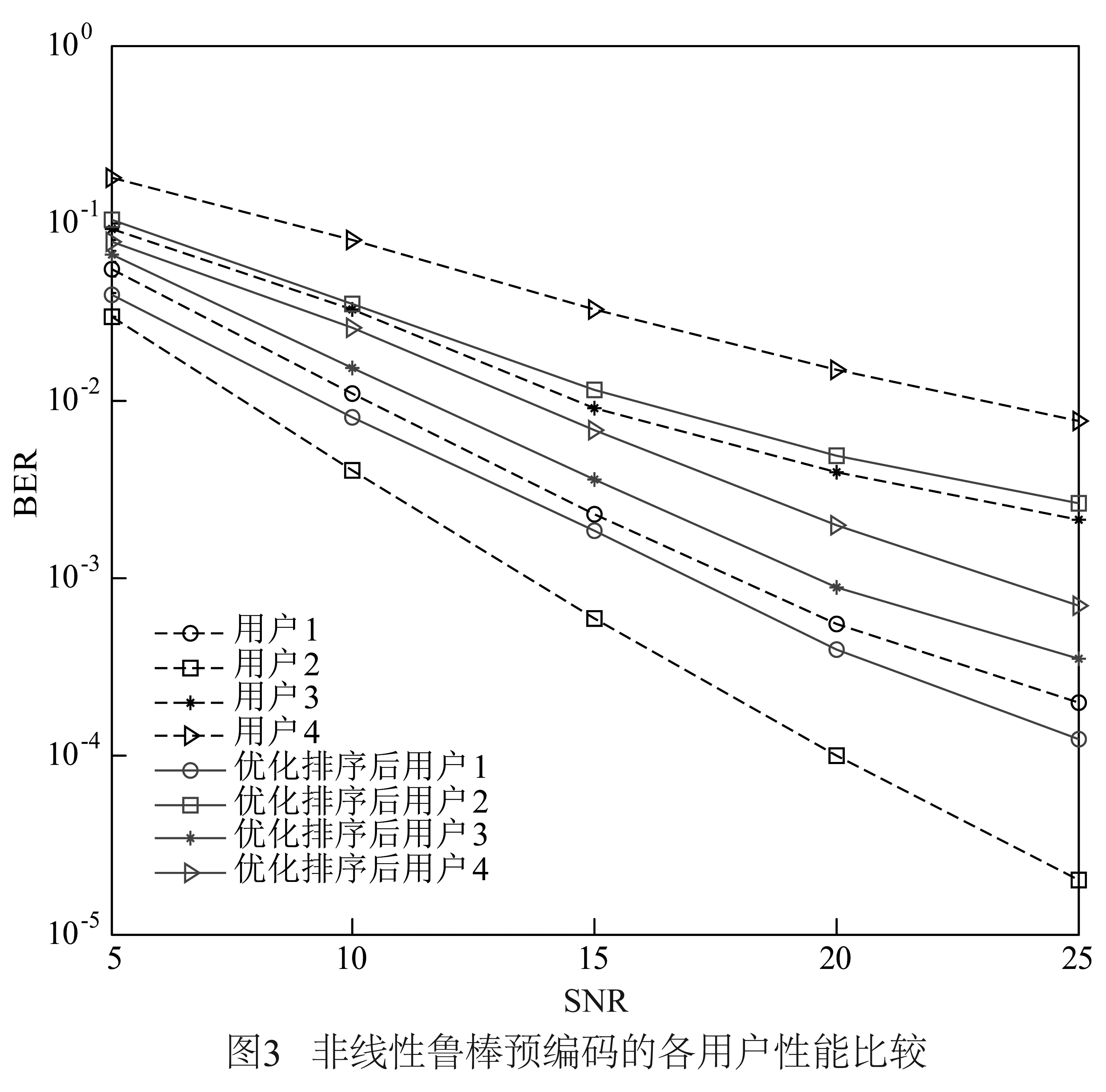
其中Ce(m,m)对应用户m接收误差的方差.可见,由于各用户信道增益大小不同,下行CSI误差的方差不同以及QR分解的正交投影先后顺序不同,各用户接收性能也存在差异.(后续仿真结果表现为不同用户的有不同的误码率).根据式(17)和式(18),可得到
E{|em|2}=Σ(m,m)R(m,m)-2
(21)
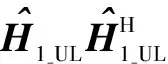
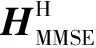
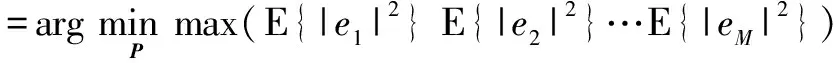
(22)
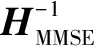
算法1 最优置换矩阵求解
输入HMMSE,Σ,M
步骤1P=0
步骤2H(1)=HMMSE
步骤3 for(i=1,…,M)
{
步骤4G(i)=(H(i))-1
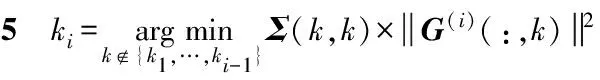
步骤6P(M-i+1,ki)=1
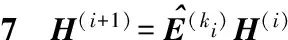
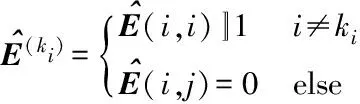
}
步骤8Popt=P,输出Popt
在通过上述算法获得最优置换矩阵Popt后,并对矩阵HMMSE实现行向量的重新排序,得到
HMMSE-NEW=PoptHMMSE
(23)

(24)
与式(17)同理,则反馈矩阵B,前馈矩阵F以及对角缩放矩阵G可重新改写为
FNEW=QNEW
(25)
另外需要注意的是由于HMMSE的不同行向量对应不同用户,则在对矩阵HMMSE实现行向量的重新排序后,同时需要对调制矢量a进行调整(aNEW=Popta),以匹配新的反馈矩阵BNEW,前馈矩阵FNEW以及对角缩放矩阵GNEW.
5 仿真及结果分析
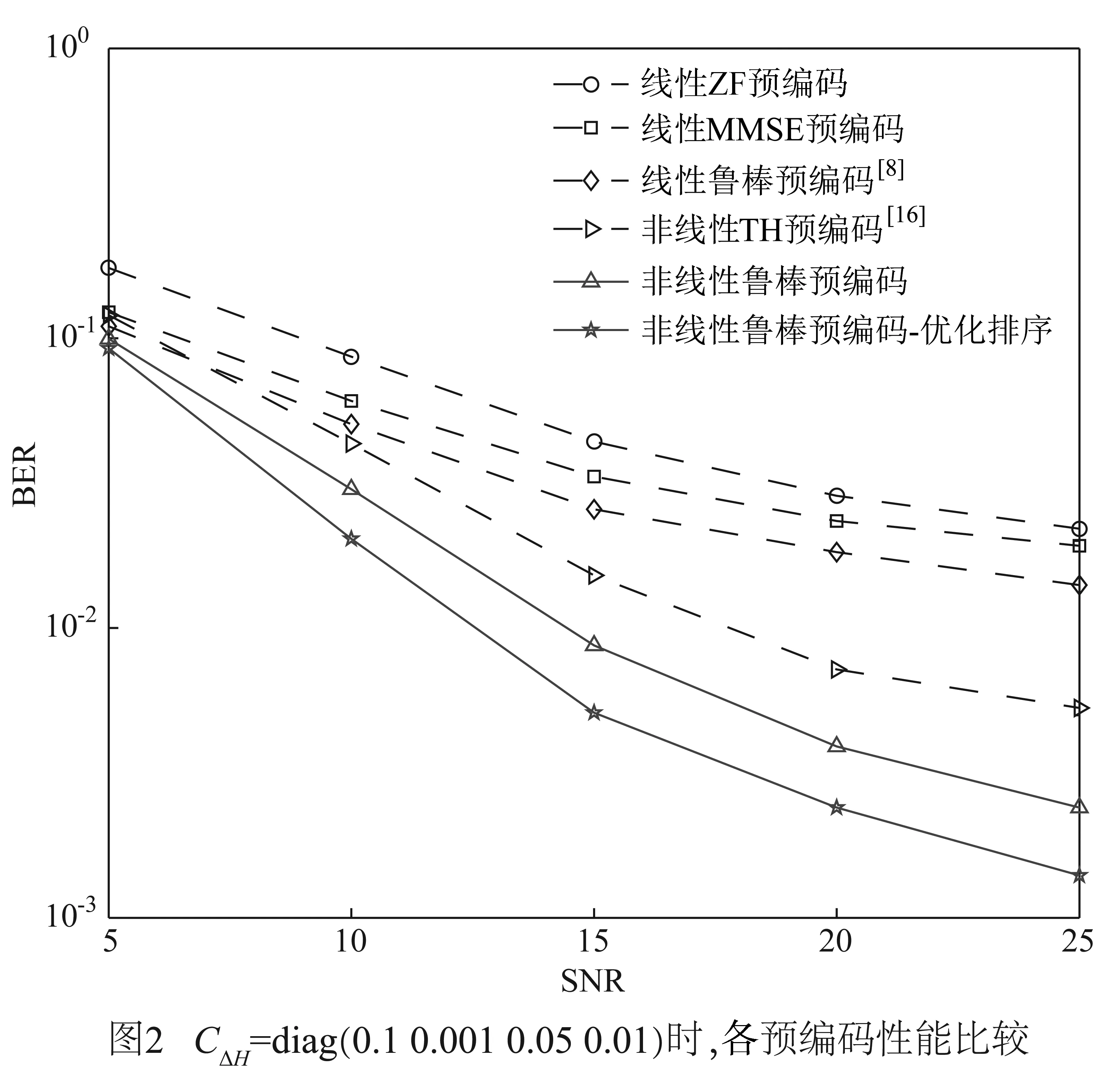
当下行CSI误差ΔH的自相关矩阵CΔH=diag{0.1 0.001 0.05 0.01}时,图2比较了ZF预编码、MMSE预编码、TH预编码[15]、线性鲁棒预编码[8]以及本文所提出的非线性鲁棒预编码与优化排序的性能.如图2所示,当存在下行CSI误差时,非线性预编码性能仍优于线性预编码性能.相对于传统的TH预编码,本文所提出的非线性鲁棒预编码利用下行CSI误差的二阶统计特性,获得了平均3dB的性能增益.同时,基于非线性鲁棒预编码的优化排序可以使非线性鲁棒预编码的误码率进一步降低,使其再获得平均2dB的性能增益.
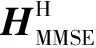
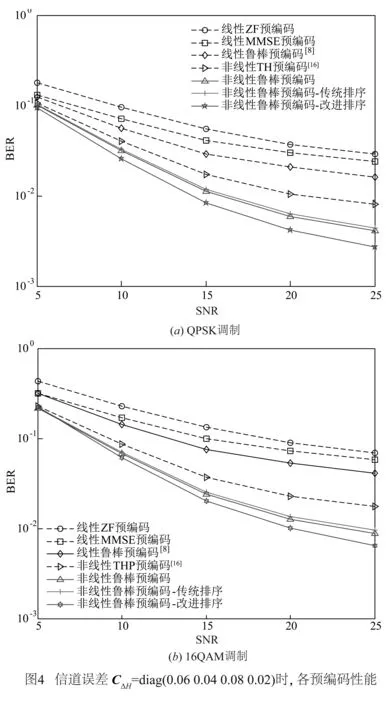
当CΔH=diag{0.06 0.04 0.08 0.02}时,图4再次比较了ZF预编码、MMSE预编码、TH预编码、线性鲁棒预编码以及本文所提出的非线性鲁棒预编码与优化排序的性能.对比图4与图2,首先我们发现随着下行CSI误差的增大,各预编码算法的误码率均有所提升.这说明无论是已有的线性鲁棒预编码还是本文提出的非线性鲁棒预编码,都无法完全消除下行CSI误差对联合传输的影响.同时,随着下行CSI误差的增大,非线性预编码对线性预编码的性能增益减小.这说明与线性预编码相比,非线性预编码对下行CSI误差更敏感.然后,我们发现随着下行CSI误差的增大,非线性鲁棒预编码针对传统的TH预编码的性能增益增加为5dB左右.这说明非线性鲁棒预编码对下行CSI误差具有一定鲁棒性,性能损失更小.最后,我们发现由于CΔH对角元素的差异变小,则各用户的性能差异也变小,则优化排序获得的增益降低到1dB左右.最后,仿真将调制星座由QPSK变为16QAM.由于基站发射功率固定,则采用更高阶的调制,会造成调制符号中每比特能量的降低,从而导致误码率升高.如图4(b)所示,各预编码的性能损失在3dB左右,同时非线性鲁棒预编码和排序算法的增益收窄.然而对于非线性预编码而言,采用更高阶的调制在理论上能降低非线性操作所带来的成形损失(shaping loss)和取模损失(module loss)[14],提高非线性预编码的性能.因此,如何在下行CSI误差条件下为非线性预编码选取最优的调制星座是值得进一步研究的问题.由于篇幅有限,该问题留作后续工作,在本文中就不再深入讨论.
6 结束语
对于实际的协作多点系统,协作基站与中央控制单元难以获得理想的下行CSI.而下行CSI误差会对预编码算法造成恶劣影响,大幅降低联合传输性能.为了避免下行CSI误差对联合传输带来的性能损失,本文利用下行CSI误差的二阶统计特性,设计了非线性鲁棒预编码算法.仿真结果表明当存在下行CSI误差时,本文所提出的非线性鲁棒预编码的性能优于ZF预编码和MMSE预编码的性能,优于TH预编码的性能,同时也优于文献[8]中线性鲁棒预编码的性能.通过理论分析和仿真,我们发现协作多点系统的特性和非线性鲁棒预编码的结构,会导致各用户间存在性能差异.所以本文通过优化非线性鲁棒预编码连续干扰消除的先后顺序,即对等效信道HMMSE的行向量进行从新排列,降低性能最差用户的误码率,从而降低非线性鲁棒预编码平均误码率.仿真结果表明优化排序能帮助非线性鲁棒预编码获得更大的性能增益.
[1]Jungnickel V,Manolakis K,Zirwas W,et al.The role of small cells,coordinated multipoint,and massive MIMO in 5G[J].IEEE Communications Magazine,2014,52(5):44-51.
[2]Lee D,Seo H,Clerckx B,et al.Coordinated multipoint transmission and reception in LTE-advanced:deployment scenarios and operational challenges[J].IEEE Communications Magazine,2012,50(2):148-155.
[3]Sheu J S,Hsieh C H.Joint preprocessing techniques for downlink CoMP transmission in multipath fading channels[A] 2012 IEEE 75th Vehicular Technology Conference (VTC Spring) [C].Yokohama,Japan:IEEE,2012.1-5.
[4]Yang C,Han S,Hou X,et al.How do we design CoMP to achieve its promised potential?[J].IEEE Wireless Communications,2013,20(1):67-74.
[5]Rui Y,Li M,Cheng P,et al.Achievable rates of coordinated multi-point transmission schemes under imperfect CSI[A] 2011 IEEE International Conference on Communications (ICC 2011)[C].Kyoto,Japan:IEEE,2011.473-479.
[6]Tajer A,Prasad N,Wang X.Robust linear precoder design for multi-cell downlink transmission[J].IEEE Transactions on Signal Processing,2011,59(1):235-251.
[7]Lagen S,Agustin A,Vidal J.Distributed inter-custer interference management for CoMP-based cellular networks[A].2013 IEEE Global Communications Conference (Globecom 2013)[C].Atlanta,USA:IEEE,2013.4204-4205
[8]Bogale T E,Vandendorpe L,Chalise B K.Robust transceiver optimization for downlink coordinated base station systems:distributed algorithm[J].IEEE Transactions on Signal Processing,2012,60(1):337-350.
[9]Castanheira D,Silva A,Gameiro A.Linear and nonlinear precoding schemes for centralized multicell MIMO-OFDM systems[J].Wireless Personal Communications,2013,72(1):759-777
[10]3GPP,TS 36.211 Physical channels and modulation[S].2010.
[11]Marsch P,Fettweis G P.Coordinated multi-point in Mobile Communications:from Theory to Practice[M].UK:Cambridge University Press,2011.
[12]Windpassinger C,Fischer R F H,Vencel T,et al.Precoding in multiantenna and multiuser communications[J].IEEE Transactions on Wireless Communications,2004,3(4):1305-1316.
[13]斯蒂芬 凯伊,等.统计信号处理基础:估计与检测理论[M].北京:电子工业出版社,2003.
[14]张贤达.矩阵分析与应用 [M].北京:清华大学出版社,2004. Zhang Xian-da.Matrix Analysis and Applications[M].Beijing:Tsinghua University Press,2004.
[15]Liu J,Krzymien W A.A novel nonlinear joint transmitter-receiver processing algorithm for the downlink of multiuser MIMO systems[J].IEEE Transactions on Vehicular Technology,2008,57(4):2189-2204

顾浙骐 男,1984年生于重庆,电子科技大学通信抗干扰技术国家级重点实验室博士研究生,研究方向为协作通信、预编码、信道互易性.
E-mail:guzheqi@163.com

张忠培 男,1967年生于重庆,电子科技大学通信抗干扰技术国家级重点实验室教授,博士生导师,博士,研究方向为无线通信、信道编码.
E-mail:Zhangzp@UESTC.edu.cn
Nonlinear Robust Precoding for Coordinated Multipoint Downlink Transmission
GU Zhe-qi,ZHANG Zhong-pei
(NationalKeyLaboratoryofScienceandTechnologyonCommunication,UniversityofElectronicScienceandTechnologyofChina,Chengdu,Sichuan611731,China)
The performance of the joint transmission in a coordinated multi-point system is bottlenecked by the downlink channel state information errors.To avoid the performance degradation of the joint transmission,a nonlinear robust precoding algorithm is proposed,which utilizes the statistical characteristics of the downlink channel state information errors.Due to the feature of the coordinated multi-point system and the structure of the nonlinear robust precoding algorithm,performance differences exist among user equipments.To improve the bit error rate of the worst performance user and reduce the average bit error rate of the nonlinear robust precoding algorithm,the order of the successive interference cancellation of the nonlinear robust precoding algorithm is also optimized.Simulation results show that the nonlinear robust precoding algorithm proposed in this paper can achieve better performance than the traditional linear and nonlinear precoding algorithms when the downlink channel state information errors exist.Simulation results also show that the ordering optimization can help the nonlinear robust precoding algorithm to attain better performance advantage.
wireless communication;coordinated multipoint;non-linear robust precoding
2014-09-03;
2016-05-14;责任编辑:梅志强
国家自然科学基金资助项目(No.61101092),国家高技术研究发展计划(863计划)(No.2014AA01A704)
TN911.6
A
0372-2112 (2016)12-2997-07
��学报URL:http://www.ejournal.org.cn
10.3969/j.issn.0372-2112.2016.12.026

