脉冲噪声环境下基于宽带模糊函数的双基地MIMO雷达目标参数估计新方法
李 丽,邱天爽
(1.大连大学信息工程学院,辽宁大连 116622; 2.大连理工大学电子信息与电气工程学部,辽宁大连 116024)
脉冲噪声环境下基于宽带模糊函数的双基地MIMO雷达目标参数估计新方法
李 丽1,邱天爽2
(1.大连大学信息工程学院,辽宁大连 116622; 2.大连理工大学电子信息与电气工程学部,辽宁大连 116024)
以Alpha稳定分布作为噪声模型,研究了脉冲噪声环境下宽带双基地MIMO雷达系统中参数估计问题.针对在脉冲噪声环境中,基于传统的信号模型和算法效果显著退化的问题,本文提出了基于分数低阶统计量的宽带模糊函数算法.首先根据分数低阶宽带模糊函数的峰值点实现对多普勒频率尺度因子和时延的联合估计.接下来基于分数低阶宽带模糊函数构造两个子阵.通过采用改进的MUSIC算法和ESPRIT算法实现了收发角的联合估计.仿真实验表明本文算法具有很好的性能.
双基地MIMO雷达;Alpha稳定分布;分数低阶宽带模糊函数;FLWBAF-MUSIC算法;FLWBAF-ESPRIT算法
1 引言
多输入多输出MIMO雷达是一种新体制雷达,是目前国际上的研究热点.按照阵元天线配置距离及方式不同,MIMO雷达可分成两大类:一是统计MIMO雷达,发射阵列和接收阵列由多个距离很远的发射阵元和接收阵元组成,并且发射阵元互不相关,接收阵元非相参处理,使得每个目标具有不同的雷达散射面积(RCS)值.二是相干MIMO雷达,发射阵列和接收阵列的各个阵元间距较小且集中放置,发射阵元发射相互正交信号,同时所有的发射接收天线对具有相同的RCS值,相干MIMO雷达利用接收阵列收到的回波信号间具有的相干特性,并借助匹配滤波器进行信号分离.本文主要研究的是第二类相干MIMO雷达的参数估计问题[1~3].
目标参数估计和定位是雷达信号处理的一个重要内容.现有的双基地MIMO雷达参数估计大都是基于窄带信号模型进行参数估计.例如,文献[4]利用发射阵和接收阵的平移不变结构,采用经典的ESPRIT算法估计目标的2维方位角,但需要额外的2维参数配对过程.文献[5]提出了一种基于平行因子分析的双基地MIMO雷达收发角及多普勒频率的联合估计算法.文献[6]通过多径信号的散列函数来估计多普勒频移和时间延迟.对宽带双基地雷达目标参数估计的方法,许多学者也进行了大量研究,然而,这些方法存在一定局限性.文献[7,8]分别基于循环相关特性和宽带模糊函数提出了宽带回波信号的Doppler和多径时延联合估计的方法,但是没能实现收发角的估计,然而收发角对于目标的精确定位也是非常重要的.文献[9]根据宽带模糊函数仅仅实现了DOA角度的估计,文献[10]基于相关信号子空间提出了声学信号的DOA估计方法.文献[11]提出基于分数阶功率谱的参数联合估计算法.虽然这些方法都具有较好的性能,然而对宽带双基地MIMO雷达收发角和多普勒频率联合估计的研究较少[11].因此宽带双基地MIMO雷达系统中参数的联合估计是研究的薄弱环节.
目前大多数的参数估计方法都是设定噪声为高斯白噪声.然而,理论研究和实际测量结果发现,雷达、声纳和无线通信系统的实际噪声中含有大量脉冲成分.在这情况下采用高斯噪声的信号模型是不合适的,这类噪声更适合用Alpha稳定分布模型来描述.为了克服这些不足,本文构造了含有脉冲噪声的新的宽带信号模型,将具有抑制脉冲噪声作用的分数低阶矩理论和具有时频特性的宽带模糊函数相结合,提出了基于分数低阶统计量的宽带模糊函数实现α稳定分布环境下双基地MIMO雷达目标参数较好估计.
2 信号模型
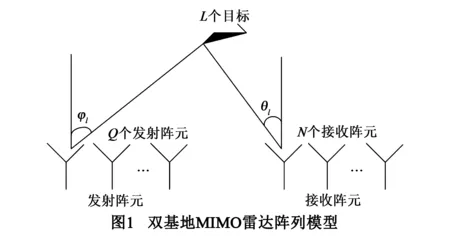
本文所用的双基地MIMO雷达系统结构如图1所示.发射和接收阵元数目分别为Q和N,阵元间距分别为dt和dr,设雷达工作在宽带远场条件,发射阵列和接收阵列处于同一相位中心.假设在相同距离分辨单元上存在L个目标,(φl,θl)表示第l个目标所对应的雷达发射角和接收角.为了提高抗干扰性,考虑发射阵元发射信号为线性调频信号,在宽带条件下,由于目标运动使得雷达接收到的回波信号除了产生多普勒频移之外,还会产生信号的尺度变换,即产生多普勒展宽.因此第n个接收阵元接收到的回波信号可表示为:
+wn(t), 0≤t≤T
(1)
其中xq(t)=exp[j2π(f0t+μt2/2)]为第q个发射阵元发射LFM信号,βl表示第l个目标的幅度衰减因子,σl和τl为第l个目标产生的多普勒频移尺度因子[10~12]和时间延迟.Aq(φl)=exp(j2π(q-1)dtsinφl/λ)称为发射导向变量,Bn(θl)=exp(j2π(n-1)drsinθl/λ)为接收导向变量,λ为发射信号波长,假设发射阵元间距和接收阵元间距均为等间隔,dt=dr=λ/2,噪声wn(t)是标准SαS稳定分布噪声.
由于有限长LFM信号的Wigner分布在时频平面上呈现为斜直线的背鳍形分布,因此,若在与该斜直线相垂直的分数阶域上求信号的分数阶傅里叶变换,则在该域的某点会出现明显的峰值.本文根据文献[12,13]中提出的分数域内的带通滤波器,选择合适的带宽,将回波信号在分数域内通过带通滤波器进行信号提取,再进行分数阶傅里叶反变换回时间域,就可提取到想要的回波信号rqn(t):
(2)
其中rqn(t)表示第q个发射阵元发射LFM信号经L个目标反射后到达第n个接收阵元的单次回波信号,rqn∈[r11,…,r1N,…,rq1,…,rqN,…,rQ1,…,rQN].
3 基于分数低阶统计量的宽带模糊函数分析
3.1 宽带模糊函数
为了实现联合估计时延和多普勒频率因子,Swick[14,15]给出了宽带模糊函数(Wide-Band Ambiguity Function,WBAF)的定义
(3)
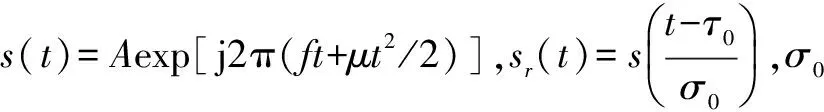
根据Schwarz不等式,我们可以得到下面的表达式
(4)
根据式(4),当τ=τ0和σ=σ0时宽带模糊函数才具有最大值,因此我们可以得到下面的关系式
(5)
3.2 Alpha稳定分布
理论研究和实际测量发现,自然界及许多工程领域的噪声存在脉冲特性,可以采用具有厚拖尾的α稳定分布过程[16,17]来描述.但是,由于一个特征指数为α(α≤2)的稳定分布过程只存在有限的小于特征指数α的矩,因此,许多传统参数估计算法在稳定分布脉冲噪声条件下性能退化严重.Alpha稳定分布(Alpha-Stable Distribution,常简称为“稳定分布”),是描述上述随机过程的最有潜力和最具吸引力的模型之一.
如果随机变量X存在参数0<α≤2,γ≥0,-1≤β≤1和实数a使其特征函数具有式(6)的形式
φ(ω)=exp{jaω-γ|ω|α[1+jβsgn(ω)ψ(ω,α)]}
(6a)
或表示为
φ(ω)=exp{jaω-σα|ω|α[1+jβsgn(ω)ψ(ω,α)]}
(6b)
式中
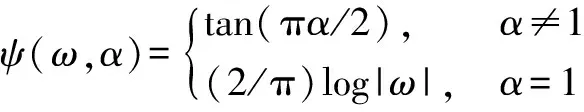
(6c)
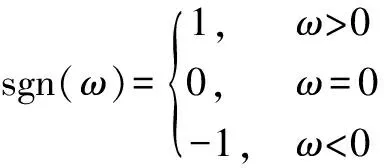
(6d)则随机变量X服从稳定分布.其中α∈(0,2]称为特征指数,它决定该分布脉冲特性的程度.α值越小,所对应分布的拖尾越厚,因此脉冲特性越显著.相反,随着α值变大,所对应分布的拖尾变薄,且脉冲特性减弱.当α=2时,为高斯分布,是α稳定分布的一个特例.γ>0为分散系数,-1<β<1称为对称参数,a称为位置参数.
分数低阶统计量(the fractional lower-order statistics,FLOS)是研究Alpha稳定分布环境下最基本的理论.对于满足0<α≤2的联合SαS分布的随机变量X和Y,其位置参数a=0,则X和Y的p阶分数低阶相关定义为
(7)
其中,p为分数低阶统计量的阶数,当p=2时p阶分数低阶相关就为通常的二阶相关.
3.3 分数低阶宽带模糊函数
从定义式(3)可以看出,传统的宽带模糊函数是基于二阶矩的.如果信号中含有α<2的脉冲噪声,其宽带模糊函数将会发散.为了解决脉冲噪声环境下信号参数估计问题,本文将分数低阶统计量和宽带模糊函数相结合,提出了基于分数低阶统计量的宽带模糊函数(the wide-band ambiguity function basing on the fractional lower-order statistics,FLOS-WBAF,即分数低阶宽带模糊函数),其定义式为:
(8)
其中(·)〈p〉=|·|〈p-1〉(·)*,(·)*表示复共轭.
图2给出了脉冲噪声环境下的信号的分数低阶宽带模糊函数和传统的宽带模糊函数的三维图.从图中可以看出,分数低阶宽带模糊函数相对于传统的宽带模糊函数能够很好的抑制脉冲噪声的干扰.
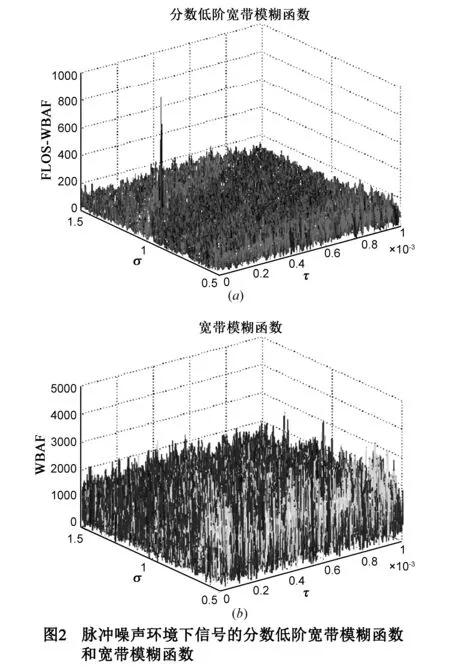
4 基于FLOS-WBAF的参数联合估计方法
本节以第q个发射信号经第l个目标反射后在第n个接收阵元的回波信号经匹配滤波后的输出rqnl(t)为例具体描述本文提出的参数估计算法,根据式(2)得rqnl(t)的表达式如下
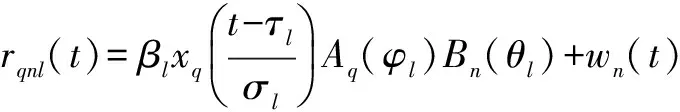
l=1,…,L
(9)
4.1 多普勒频移因子及时延的联合估计
根据本文提出的FLOS-WBAF定义,我们可以得到
(10)
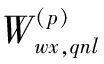
根据式(4),(5)和(10),我们可以得到
(11)
其中τl0,σl0分别为分数低阶宽带模糊函数峰值点对应的横纵坐标,即第l个目标的时延和多普勒频移尺度因子.
4.2 发射角和接收角的估计
根据式(11),定义变量yql(t)为
(12)
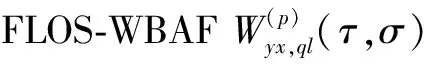
(13)
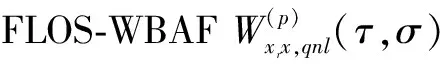
(14)
(15)
在第l个目标反射的回波信号的分数低阶宽带模糊函数的峰值点(τl0,σl0)处,
+Nn(τl0,σl0)
(16)
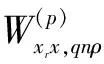
(17)
取L个FLOS-WBAF的峰值点作为该阵元的观测数据,则在第n个阵元上的空间时频输出为
(18)
根据式(17)和(18),将所有阵元的空间时频输出表示为向量形式,即可得到基于分数低阶宽带模糊函数的空间时频分布数据模型
P=BAZ+N
(19)
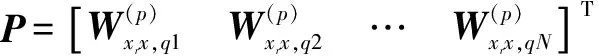
(20)
(21)
(22)
(23)
其中
(24)
本文构造两个子阵P1和P2,两个子阵的空间时频输出的数据模型为
P1=BZ+N1,q=1
(25)
P2=BAZ+N2,q≠1
(26)
式(25)的分数低阶自相关矩阵定义为
(27)
由于信号与噪声不相关,且信号与噪声相互独立,式(27)可以写成下面的形式
(28)
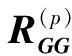
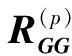
(29)
其中UG和UN分别是信号子空间和噪声子空间.
利用分数低阶宽带模糊函数相关矩阵代替传统的阵列相关矩阵,并可根据MUSIC算法得到FLWBAF-MUSIC空间谱为:
(30)
对P(θ)进行谱峰搜索,可得到第l个目标发射回波信号的接收角的估计值θl.
定义两个矩阵C11和C12,
(31)
和
(32)

根据式(31)和(32),我们可以得到如下的表达式
(33)
其中()#表示伪逆矩阵.
由于接收角θl已经由式(30)估计得到,因此矩阵A也可以写成下面的形式
(34)
因此发射角的估计值φl可以根据FLWBAF-ESPRIT算法,由下面的表达式估计得到
φl=arcsin(arg(gl)/(q-1)π)
(35)
其中gl是矩阵A主对角线上的元素,arg(gl)表示取gl的相位角.
4.3 时间复杂度分析
本文算法通过对分数低阶宽带模糊函数峰值搜索实现了多普勒频移尺度因子和时延的联合估计.因此这两个参数估计的时间复杂度约为O(P2).对收发角的联合估计是将空间时频分布和阵列信号处理相结合,并且本文算法先估计DOA角再估计DOD角,因此FLWBAF-MUSIC算法的时间复杂度约为O(N3+JNL),FLWBAF-ESPRIT算法的时间复杂度约为O(N3+JNL+Q3),其中Q为发射阵元数目,N为接收阵元数目,J为MUSIC谱数目,L为目标个数,P为快拍数.
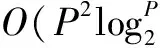
5 仿真实验及分析
仿真实验参数设置,发射阵元和接收阵元数目分别为Q=4和N=6,目标个数为L=2,相对于发射阵元和接收阵元的发射角和接收角分别为(φ1,θ1)=(20°,30°),(φ2,θ2)=(50°,60°),多普勒频移尺度参数a1=0.9,a2=1.1,多径时延分别为τ1=80/fs,τ2=160/fs.两个LFM信号的初始频率、频率调制率及幅度分别为f10=0.25MHz,μ10=100MHz,A1=2,f20=0.3MHz,μ20=-200MHz,A2=4,初相φ10=0,φ20=0,采样频率为fs=1MHz,采样点数为1000,Monte-Carlo实验次数为300.
5.1 分数低阶矩p
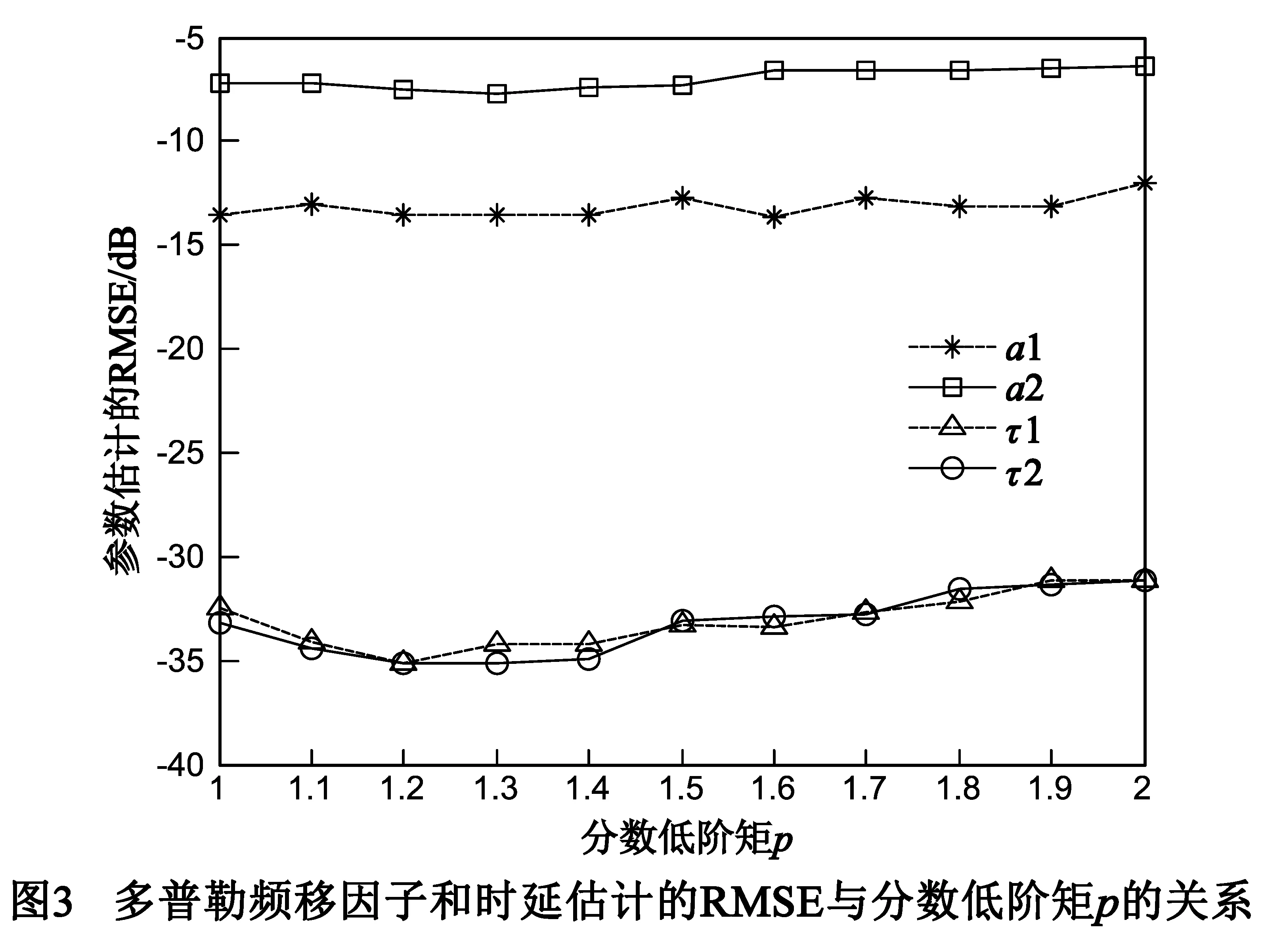
本次实验中,Alpha稳定分布噪声的特征指数α=1.4,广义信噪比GSNR=-10dB.图3显示了多普勒频移因子及时延估计的RMSE与分数低阶矩p的关系.
从图3可以看出,当分数低阶矩1.1≤p≤1.4时本文算法的具有较好性能.由Alpha稳定分布的特性可知,一个特征指数为α的稳定分布过程只存在有限的小于特征指数α的矩.由图3我们能发现分数低阶矩p≥1.5时,参数估计的RMSE变大.因此,后续实验中,阶数p取值为1.1≤p<α.
5.2 广义信噪比GSNR
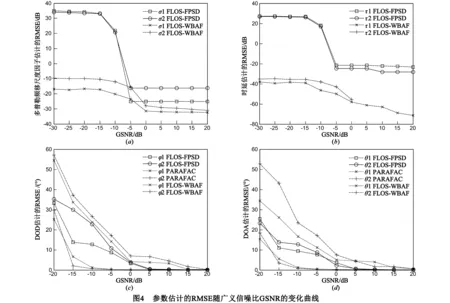
本次实验中,Alpha稳定分布噪声的特征指数设定为α=1.4,分数低阶矩设定为p=1.1.图4(a)~(b)显示了本文算法与FLOS-FPSD算法[11]关于多普勒频率因子和时延估计的RMSE随GSNR变化的曲线.图4(c)~(d)显示了本文算法与PARAFAC算法[5]、FLOS-FPSD算法关于收发角估计的RMSE与GSNR之间的关系.
从图4(a)和(b)中可以看出,本文方法具有较好的估计性能,通过与其他两种算法进行比较,我们能发现本文算法的估计性能显著优于FLOS-FPSD方法和PARAFAC算法.图4(c)和(d)显示了本文方法、PARAFAC方法和FLOS-FPSD算法关于收发角估计RMSE随GSNR的变化曲线.从图中可以看出,当GSNR大于-15dB时,本文算法RMSE很小,并保持稳定.本文算法将分数低阶统计量理论应用到了参数估计的算法中,由于分数低阶统计量具有很好的抑制脉冲噪声的性能,同时宽带模糊函数很好的能量聚集特性,而随机噪声不具有这一特性,因此本文提出的FLOS-WBAF算法不仅能够很好的抑制脉冲噪声的干扰,而且具有很好参数估计性能.实验证明,本算法在低GSNR时仍具有很好的性能.5.3 Alpha稳定分布噪声的特征指数α
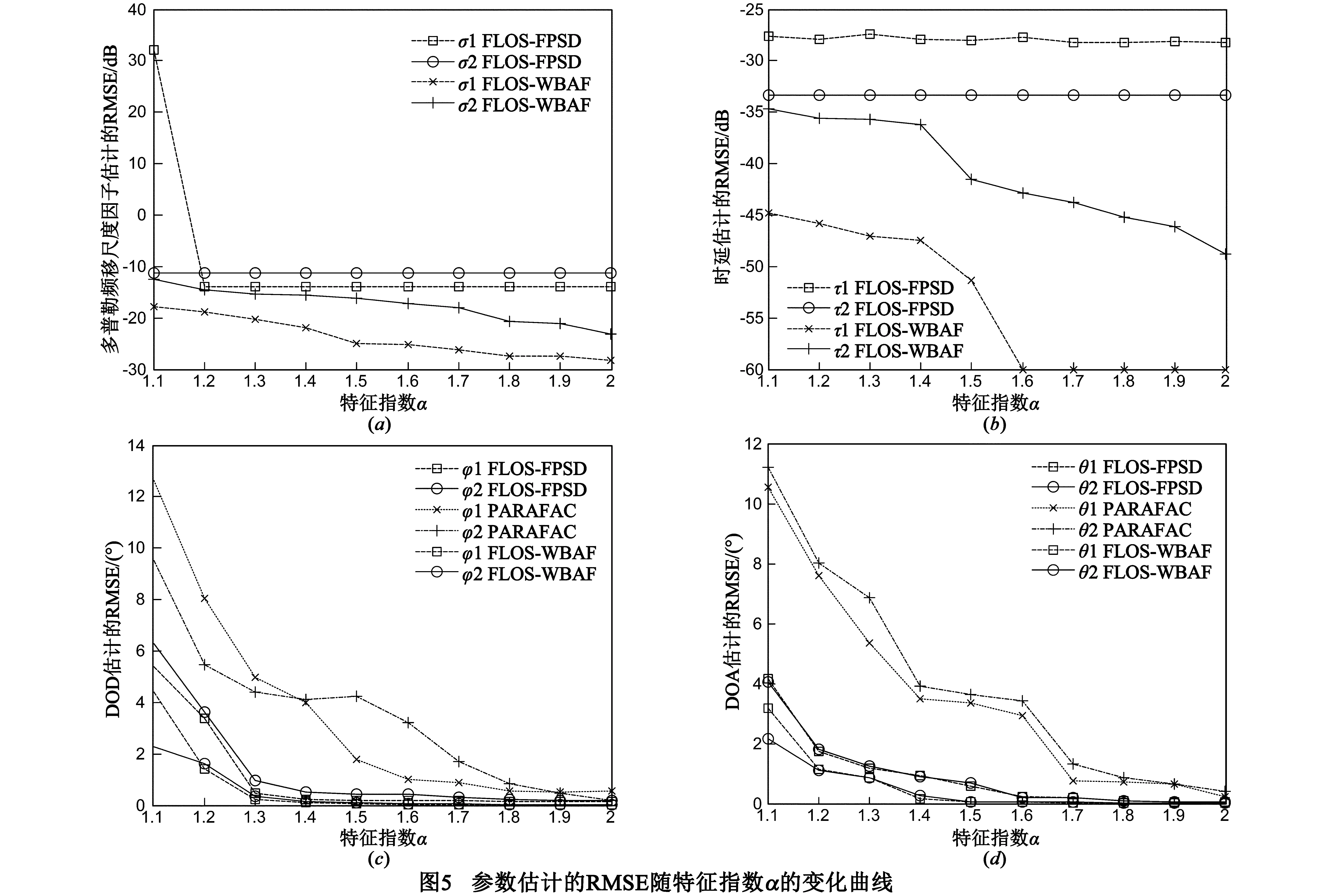
在本次实验中,广义信噪比设定为GSNR=-10dB.图5显示了三种算法对不同参数估计的RMSE随噪声特征指数α变化的曲线,其中特征指数α的变化范围为[1.1,2].
从图5可以看出,在脉冲噪声环境下,本文FLOS-WBAF算法的参数估计性能明显优于FLOS-FPSD算法和PARAFAC算法.本文提出的FLOS-WBAF算法不仅能够很好的抑制脉冲噪声的干扰,而且具有很好参数估计性能.而PARAFAC算法在进行参数估计时没有考虑脉冲噪声的影响,因此在脉冲噪声环境下,本文算法的性能明显优于其他两种算法.
6 结论
本文提出了一种基于分数低阶宽带模糊函数的双基地MIMO雷达目标参数估计的新方法.在双基地MIMO雷达中,本文选用线性调频信号作为发射信号,利用其具有大时宽频宽积特性,可获得更好的低截获概率特性.针对雷达回波信号中常含有大量脉冲噪声,提出了含有脉冲噪声的宽带信号模型,并提出了分数低阶宽带模糊函数算法实现目标参数估计.首先,通过FLOS-WBAF峰值搜索实现了多普勒频移因子和时延的联合估计.接下来,在时频域内构造基于分数低阶宽带模糊函数的两个子阵,采用本文提出的FLWBAF-MUSIC和FLWBAF-ESPRIT算法实现了接发角的联合估计.仿真实验证明在较低的GSNR环境下本文提出的方法仍具有较低的RMSE,具有很好的性能.
[1]Fishler E,Haimovich A,Blum R S,et al.Spatial diversity in radars models and detection performance[J].IEEE Transactions on Signal Processing,2006,54(3):823-838.
[2]Stoica P,Li J,Xie Y.On probing signal design for MIMO radar[J].IEEE Transactions on Signal Processing,2007,55(8):4151-4161.
[3]陈浩文,黎湘,庄钊文.一种新兴的雷达体制—MIMO雷达[J].电子学报,2012,40(6):1190-1198. Chen H W,Li X,Zhuang Z W.Arising radar system—MIMO radar[J].Acta Electronica Sinica,2012,40(6):1190-1198.(in Chinese)
[4]Chen D F,Chen B X,Qi G D.Angle estimation using ESPRIT in MIMO radar[J].Electronics Letters,2008,44(12):770-771.
[5]张剑云,郑志东,李小波.双基地MIMO雷达收发角及多普勒频率的联合估计算法[J].电子与信息学报,2010,32(8):1843-1848. Zhang jinyun,Zheng zhidong,Li xiaobo.Multi-target localization based on polynomial rooting for bistatic MIMO radar[J].Journal of Electronics & Information Technology,2010,32(8):1843-1848.(in Chinese)
[6]Zaition S,Ahmad Z S.Estimation of the Doppler spread and time delay spread for the wireless communication channel[A].2010 International Conference on Computer Applications and Industrial Electronics (ICCAIE 2010)[C].Kuala Lumpur,Malaysia,2010.438-442.
[7]史建锋,王可人.基于循环相关的LFM脉冲雷达宽带回波Doppler和多径时延的联合估计[J].电子与信息学报,2008,30(7):1736-1739. Shi Jianfeng,Wang Keren.Joint estimation of Doppler and multipath time delay of wideband echoes for LFM pulse radar based on cyclic correlation[J].Journal of Electronics & Information Technology,2008,30(7):1736-1739.(in Chinese)
[8]Qu J,Kon M W,Luo Z Q.The estimation of time delay and Doppler stretch of wideband signals[J].IEEE Transactions on Signal Processing,1995,43(4):904-916.
[9]Ma N,Goh J T.Ambiguity-function-based techniques to estimate DOA of broadband chirp signals[J].IEEE Transactions on Signal Processing,2006,54(5):1826-1839.
[10]Chen H W,Zhao J W.Wideband MVDR beamforming for acoustic vector sensor linear array[J].IEE Proceedings of Radar,Sonar and Navigation,2004,151(3):158-162.
[11]Li L,Qiu T S.Parameter estimation based on fractional power spectrum under Alpha-stable distribution noise environment in wideband bistatic MIMO radar system[J].AEUE-International Journal of Electronics and Communications,2013,67(11):947-954.
[12]陶然,邓兵,王越.分数阶傅里叶变换及其应用[M].北京:清华大学出版社,2009.285-296.
[13]齐林,陶然,周思永,王越.LFM信号的一种最优滤波算法[J].电子学报,2004,32(9):1464-1467. Qi Lin,Tao Ran,Zhou Siyong,Wang Yue.An approach for optimal filtering of LFM signal[J].Acta Electronica Sinica,2004,32(3):1464-1467.(in Chinese)
[14]Swick D A.An Ambiguity Function Independent of Assumpiton About Bandwidth and Carrier Feequency[R].Washington,DC:Naval Research Lab Washington DC,1966.
[15]Swick D A.A Review of Wide-Band Ambiguity Function[R].Washington,DC:Naval Research Lab Washington DC,1969.
[16]Nikias C L,SHAO M.Signal Processing with Alpha Stable Distributions and Applications[M].New York:John Wiley & Sons Inc,1995.
[17]李森,邱天爽.Alpha稳定分布噪声中的韧性投影近似子空间跟踪算法[J].电子学报,2009,37(3):519-522. Li Sen,Qiu Tianshuang.A robust PAST Algorithm in alpha stable noise environment[J].Acta Electronica Sinica,2009,37(3):519-522.(in Chinese)

李 丽 女,1979年生于黑龙江佳木斯.大连大学信息工程学院副教授.研究方向为阵列信号处理、参数估计.
E-mail:ffsimple@163.com
邱天爽 男,1954年生于辽宁省抚顺.大连理工大学教授,博士生导师.主要从事信号信息处理方面的教学与研究工作.
A Novel Method for Parameter Estimation Based on Wide-Band Ambiguity Function in Bistatic MIMO Radar System in Impulsive Noise Environment
LI Li1,QIU Tian-shuang2
(1.InformationEngineeringCollege,DalianUniversity.Dalian,Liaoning116622,China; 2.FacultyofElectronicInformationandElectricalEngineering,DalianUniversityofTechnology,Dalian,Liaoning116023,China)
This paper takes the Alpha stable distribution as the noise model and studies the problem of bistatic multiple-input multiple-output (MIMO) radar system in the impulsive noise environment.Since the conventional algorithms degenerate severely in the impulsive noise environment,this paper proposes a novel method of wide-band ambiguity function based on the fractional lower-order statistics (FLOS-WBAF).Firstly,Doppler stretch and time delay are jointly estimated by peak searching the FLOS-WBAF.Secondly,two sub-array models are constructed based on the FLWBAF.Furthermore,two modified algorithms are proposed for the estimation of DODs and DOAs,including the fractional lower-order wide-band ambiguity function based on MUSIC algorithm (FLWBAF-MUSIC) and the fractional lower-order wide-band ambiguity function based on ESPRIT algorithm (FLWBAF-ESPRIT).Simulation results are presented to verify the effectiveness of the proposed method.
bistatic MIMO radar;Alpha stable distribution;fractional lower-order wide-band ambiguity function;FLWBAF-MUSIC algorithm;FLWBAF-ESPRIT algorithm
2015-07-27;
2015-11-18;责任编辑:蓝红杰
国家自然科学基金(No.61401055,No.61139001,No.61172108,No.61261046)
TN911.7
A
0372-2112 (2016)12-2842-07
��学报URL:http://www.ejournal.org.cn
10.3969/j.issn.0372-2112.2016.12.005

